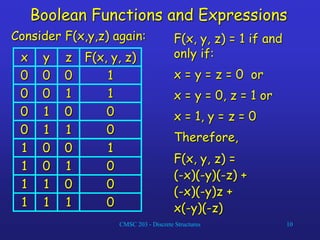
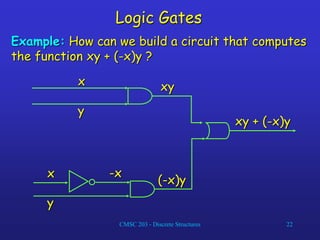
This document discusses Boolean algebra and discrete structures. It covers topics like Boolean operations, Boolean functions and expressions, logic gates, and the definition of a Boolean algebra. Specifically, it defines the operations of complement, sum, and product for Boolean algebra. It also discusses how to represent and derive Boolean functions from truth tables and discusses properties like duality and identities. Finally, it defines the basic logic gates of OR, AND, and inverter and gives an example of building a circuit to compute a Boolean function.