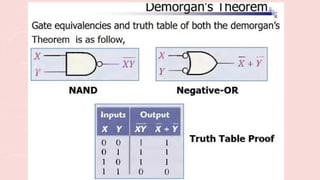
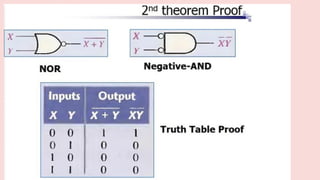
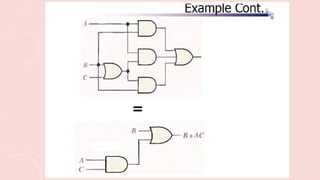
The document outlines the basic identities and principles of Boolean algebra, including commutative, associative, and distributive properties. It emphasizes the duality principle and provides simplification techniques for Boolean functions using identities. The text also illustrates how to effectively reduce the number of logic gates in digital circuits through algebraic manipulation.

1. Basic Identities of Boolean Algebra
M. Morris Mano
Edition 5
Digital Design

2. BASIC IDENTITIES OF BOOLEAN ALGEBRA
The following table lists the most basic identities of Boolean algebra
1a. X + 0
2a. X + 1
3a. X + X
= X
= 1
= X
4a. X + X’ = 1
5a. (X’)’ = X
6a. X + Y = Y + X
7a. X + ( Y + Z ) = ( X + Y ) + Z
Commutative
Associative
8a. X . ( Y + Z ) = X . Y + X . Z Distributive
9a. ( X + Y )’ = ( X’ . Y’ )
10a. X + X . Y
= X
DeMorgan
Absorption
The dual of an algebraic
expression is obtained by
• interchanging OR and
AND operation
• replacing 1s by 0s and
0s by 1s.
The other 10 identities
can be obtained by:
taking the dual of the
expressions on both
sides of the equal sign.

3. The following table lists the most basic identities of Boolean algebra
1a. X + 0
2a. X + 1
3a. X + X
= X
= 1
= X
4a. X + X’ = 1
5a. (X’)’ = X
6a. X + Y = Y + X
7a. X + ( Y + Z ) = ( X + Y ) + Z
Commutative
Associative
8a. X . ( Y + Z ) = X . Y + X . Z Distributive
9a. ( X + Y )’ = ( X’ . Y’ )
10a. X + X . Y
= X
DeMorgan
Absorption
The dual of an algebraic
expression is obtained by
• interchanging OR and
AND operation
• replacing 1s by 0s and
0s by 1s.
1b. X . 1
2b. X . 0
3b. X . X
= X
= 0
= X
4b. X . X’ = 0
6b. X . Y = Y . X
7b. X . ( Y . Z ) = ( X . Y ) . Z
8b. X + ( Y . Z ) = (X + Y) . (X + Z)
9b. ( X . Y )’ = ( X’ + Y’ )
10b. X . (X + Y) = X
The duality principle of
Boolean algebra states that
a Boolean equation remains
valid if we take the dual of
the expressions on both
sides of the equal sign.
DUAL :
BASIC IDENTITIES OF BOOLEAN ALGEBRA

33. F = X’ Y’ Z + X’ Y Z + X Y Z’ + X Y Z
Boolean algebra is a useful tool for simplifying digital circuits. Consider the Function
F = X’ Z (Y+ Y’) + X Y (Z’ + Z)
F = (X’ Z) . 1 + (X Y) . 1
Y + Y’ = 1
(X’ Z) . 1 = X’ Z (X Y) . 1 = X Y
F = X’ Z + X Y
( Using Identity: X + X’ = 1 )
SIMPLIFICATION OF BOOLEAN FUNCTION
Algebraic Manipulation
F = X’ Y’ Z + X’ Y Z + X Y Z’ + X Y Z
This function is implemented with four AND gates and one OR gate. This can be reduced or
simplified by applying Identities.
Simplification of the function F by applying identities:
Z + Z’ = 1
( Using Identity: X . 1 = X )
Simplified Boolean Function

34. F = X’ Y’ Z + X’ Y Z + X Y Z’ + X Y Z
Boolean algebra is a useful tool for simplifying digital circuits. Consider the Function
F = X’ Z + X Y
SIMPLIFICATION OF BOOLEAN FUNCTION
Algebraic Manipulation
: Simplified Boolean Function
: Original Boolean Function
Both are Same : Defining same Truth Table (Same Behavior)
1
Truth Table:
0 0
0
0 0
1
0 1
0
0 1
1
1 0
0
1 0
1
1 1
0
1 1
1
X Y Z
F
1
1
1
0
0
0
0
But Simplified Form has minimum number of gates:
2 AND and 1 OR logic gate
Minimum Gate Logic
: Minimum Number of Logic Gates
: Minimum Number of Literals

35. F = X’ Y’ Z + X’ Y Z + X Y Z’ + X Y Z
Boolean algebra is a useful tool for simplifying digital circuits. Consider the Function
F = X’ Z + X Y
SIMPLIFICATION OF BOOLEAN FUNCTION
Algebraic Manipulation
x’
y’
z
x’
y
z
x
y
z’
x
y
z
F
x’
z
x
y
F
Economical ?

36. SIMPLIFICATION OF BOOLEAN FUNCTION
1. x (x’ + y)
2. x + x’ y
3. (x + y) (x + y’)
Simplify the following Boolean functions to a minimum number of literals .

37. SIMPLIFICATION OF BOOLEAN FUNCTION
x (x’ + y)
Economical ?
= x x’ + x y
= 0 + x y
= x y
x’
y
x
x (x’ +
y)
(x’ + y)
x
y
x y
Both have same
functionality
As x x’ = 0
As 0 + A =
A
Simplify the following Boolean functions to a minimum number of literals .
1. x (x’ + y)

38. SIMPLIFICATION OF BOOLEAN FUNCTION
2. x + x’ y
x + x’ y
Economical ?
= (x + x’) . (x + y)
= 1 . (x +
y)
= (x + y)
x’
y
x
x + x’ y
x’ y
x
y
x + y
Both have same
functionality
As 1 . A = A
As x + x’ =
1
Simplify the following Boolean functions to a minimum number of literals .

39. SIMPLIFICATION OF BOOLEAN FUNCTION
3. (x + y) (x + y’)
(x + y) (x + y’) = x x + x y’ + x y + y y’
= x + x y’ + x y + 0
= x + x y’ + x y
(x+y)(x+y’)
x
As x x = x
As 0 + A =
A
x
y
(x + y)
As y y’ = 0
= x ( 1 + y’ + y)
As 1 + y’ + y = 1
= x . 1
= x
x
y’
(x + y’)
(x + y) (x + y’) = x + y y’
= x + 0
= x
Simplify the following Boolean functions to a minimum number of literals .
OR