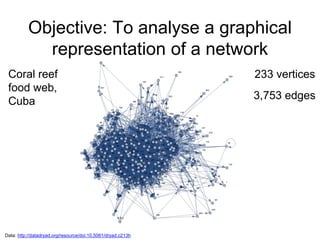
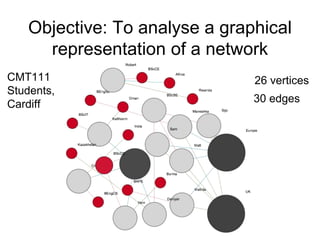
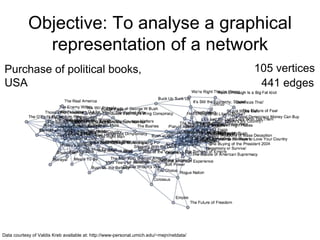
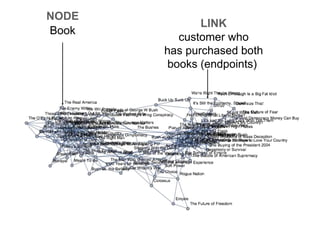
The document analyzes a network graph of purchases of political books in the USA with 105 vertices and 441 edges. It explores various graph metrics and centrality measures including degree, closeness, betweenness, and eccentricity centrality. It identifies graph properties such as the diameter of 7, radius of 4, and presence of communities detected using graph partitioning and community detection algorithms.

1. Books on Politics Network-
2004

2. Objective: To analyse a graphical
representation of a network
Coral reef
food web,
Cuba
233 vertices
3,753 edges
Data: http://datadryad.org/resource/doi:10.5061/dryad.c213h

3. Objective: To analyse a graphical
representation of a network
CMT111
Students,
Cardiff
26 vertices
30 edges

4. Objective: To analyse a graphical
representation of a network
Purchase of political books,
USA
105 vertices
441 edges
Data courtesy of Valdis Kreb available at: http://www-personal.umich.edu/~mejn/netdata/

5. Limitations
• Number of purchases missing from database
• No weights : Number of buyers co-purchased the
books

6. Mathematica
• Importing data
• Will not read as wide a variety of CSV formats as Gephi
• Can read .gml, .gv, .dot, .graphml, .gxl, .col, .g6, .s6, .gw, .net, .tgf
• Use Map or create a rule to show links (->) from one column of a CSV onto
another
• Other attributes
• More difficult to show vertex/edge attributes than in Gephi but still ppssiblt to
highlight using HighlightGraph[g, x]
• Built-in functions
• Very intuitive and well documented:
https://reference.wolfram.com/language/guide/GraphsAndNetworks.html

7. Book
customer who
has purchased both
books (endpoints)
NODE
LINK

8. This graph is
unweighted: edges do not have associated weights
undirected: all edges travel in both directions
contains loops: no vertex is linked directly to itself
simple: undirected, unweighted, loop-free and lacks multiple edges
incomplete: each vertex is not connected to every other vertex
cyclic: contains at least one cycle
not bipartite: vertices cannot be divided into two disjoint sets
UndirectedGraphQ[books]
WeightedGraphQ[books]
CompleteGraphQ[books]
SimpleGraphQ[books]
BipartiteGraphQ[books]
LoopFreeGraphQ[books]
AcyclicGraphQ[books]

9. {6, 4, 4, 23, 8, 7, 11, 8, 25, 16, 15, 18, 25, 13, 9, 5, 3, 5, 3, 5, 10, 5, 7, 9, 9,
5, 9, 9, 3, 4, 20, 11, 5, 9, 5, 10, 5, 7, 7, 8, 18, 8, 6, 5, 5, 6, 4, 18, 4, 8, 3, 6,
5, 5, 6, 4, 4, 5, 13, 5, 6, 4, 6, 4, 9, 7, 21, 6, 4, 5, 7, 15, 22, 21, 16, 16, 13, 7,
5, 8, 4, 4, 9, 8, 23, 5, 14, 5, 5, 6, 5, 8, 3, 7, 7, 4, 6, 6, 5, 12, 12, 5, 4, 2, 3}
VertexDegree[books]
Vertex degrees:
Histogram[VertexDegree[books], ChartStyle -> Blue,
AxesLabel -> {HoldForm[Vertex degree], HoldForm[Frequency]},
PlotLabel -> None, LabelStyle -> {14, GrayLevel[0]}]

10. MatrixForm[GraphDistanceMatrix[books]]
Distance matrix

11. Array plot: distance matrix
ArrayPlot[GraphDistanceMatrix[books]]

12. Max[Flatten[GraphDistanceMatrix[books]]]
OR
GraphDiameter[books]
Diameter = 7
Radius = 4
GraphRadius[books]
Maximum and minimum eccentricities of any vertex:

13. Eccentricity Centrality
HighlightGraph[books, VertexList[books],
VertexSize ->
Thread[VertexList[books] ->
Rescale[EccentricityCentrality[books]]]]
Increases as maximum distances to every other reachable node increases

14. Closeness Centrality
HighlightGraph[books, VertexList[books],
VertexSize ->
Thread[VertexList[books] ->
Rescale[ClosenessCentrality[books]]]]
Increases as average distance to other nodes increases

15. Betweenness Centrality
HighlightGraph[books, VertexList[books],
VertexSize ->
Thread[VertexList[books] ->
Rescale[BetweennessCentrality[books]]]]
Increases as node lies on more shortest paths between other node-pairs

16. Degree Centrality
HighlightGraph[books, VertexList[books],
VertexSize ->
Thread[VertexList[books] ->
Rescale[DegreeCentrality[books]]]]
Increases as vertex degree increases

17. a = ListPlot[EccentricityCentrality[books], Filling -> Axis, PlotStyle -> Red]
b = ListPlot[ClosenessCentrality[books], Filling -> Axis, PlotStyle -> Magenta]
c = ListPlot[RadialityCentrality[books], Filling -> Axis, PlotStyle -> Cyan]
d = ListPlot[DegreeCentrality[books], Filling -> Axis]
gg = GraphicsGrid[{{a, b}, {c, d}}]
Export["CentralityGrid.png", gg]
Eccentricity Closeness
Radiality Degree

18. Dual Hub
HighlightGraph[books, GraphHub[books]]
Nodes with the highest vertex degree are returned

19. Hub Neighbours
HighlightGraph[books, NeighborhoodGraph[books, GraphHub[books]]]

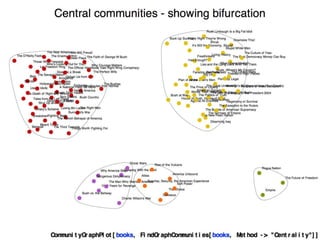
20. CommunityGraphPlot[books]
Communities: Small world graph (Modular)

21. Graph partition:
minimises number of endpoints having edges in each part
HighlightGraph[books,FindGraphPartition[books]]

22. Graph communities:
maximises edges joining nodes within communities
with relatively fewer edges joining to nodes in other
communities
HighlightGraph[books, FindGraphCommunities[books]]

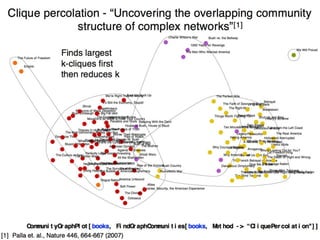
25. Cliques
Largest set of connected vertices
HighlightGraph[books, Subgraph[books, FindClique[books]]]

26. Cliques
Largest set of connected vertices within 2 edges of each other
HighlightGraph[books, Subgraph[books, FindKClique[books, 2]]]

27. Cliques
Largest set of connected vertices within 3 edges of each other
HighlightGraph[books, Subgraph[books, FindKClique[books, 3]]]

28. Cliques
Largest set of connected vertices within 4 edges of each other
HighlightGraph[books, Subgraph[books, FindKClique[books, 4]]]

29. Cliques
Largest set of connected vertices within 5 edges of each other
HighlightGraph[books, Subgraph[books, FindKClique[books, 5]]]

30. Cliques
Largest set of connected vertices within 6 edges of each other
HighlightGraph[books, Subgraph[books, FindKClique[books, 6]]]

31. Cliques
Largest set of connected vertices within 7 (=diameter)
edges of each other
HighlightGraph[books, Subgraph[books, FindKClique[books, 7]]]

32. Lessons & Conclusions
• Mathematica Vs Gephi on Data Visualization
• Gephi struggles with larger datasets, crashes on OS X, cannot ‘undo’
• Gephi good a pulling apart larger datasets for easier visualisation, takes a wider range of input
formats, can visualise ‘multiple graphs’ more easily
• All the other functions within Mathematica at your disposal to aid network analysis e.g. Plot
• Source of Data Sets
• Working with a dataset of sufficient size but not so big that it cannot be comprehended.
• Analysis of sub-networks