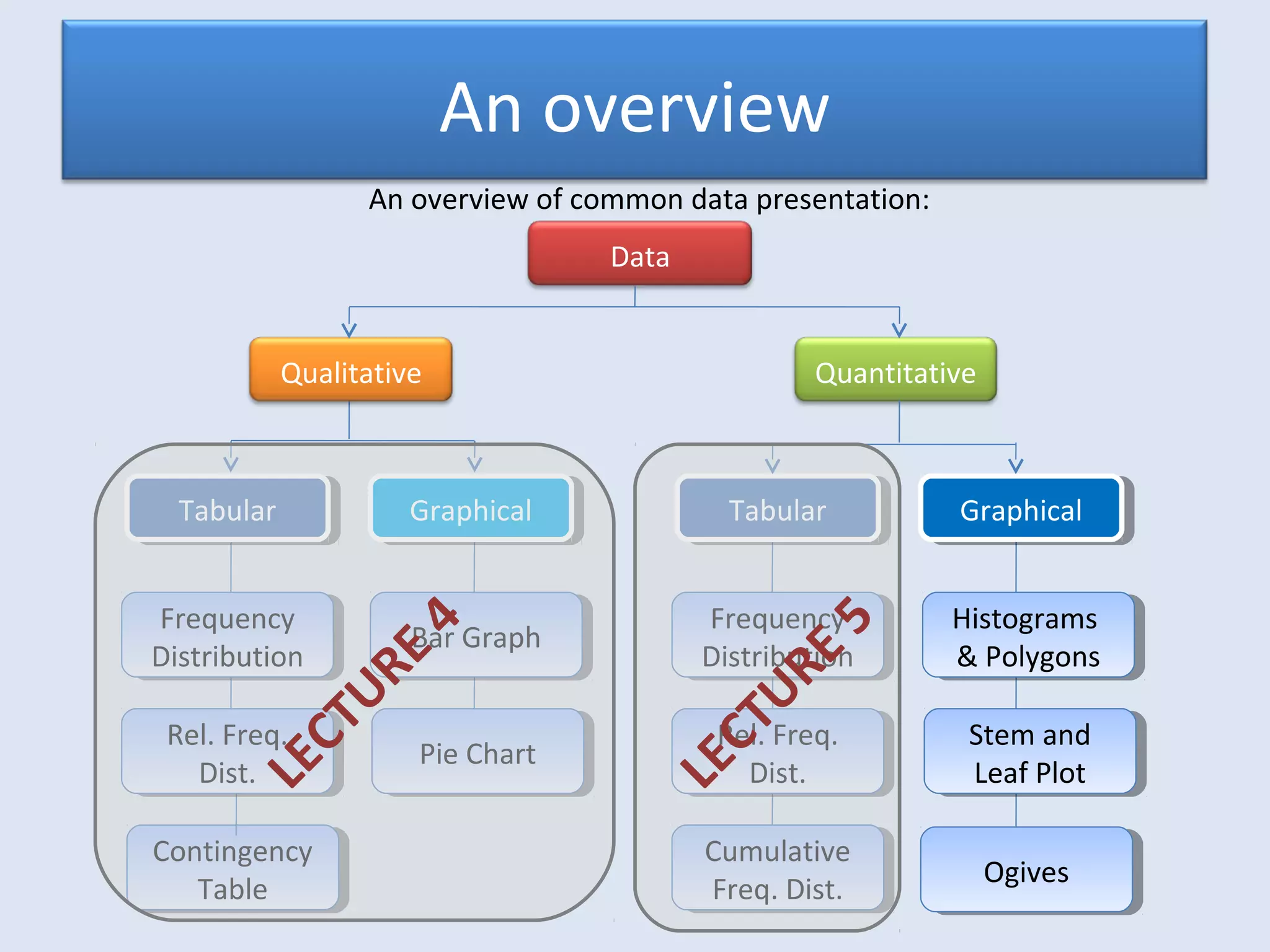
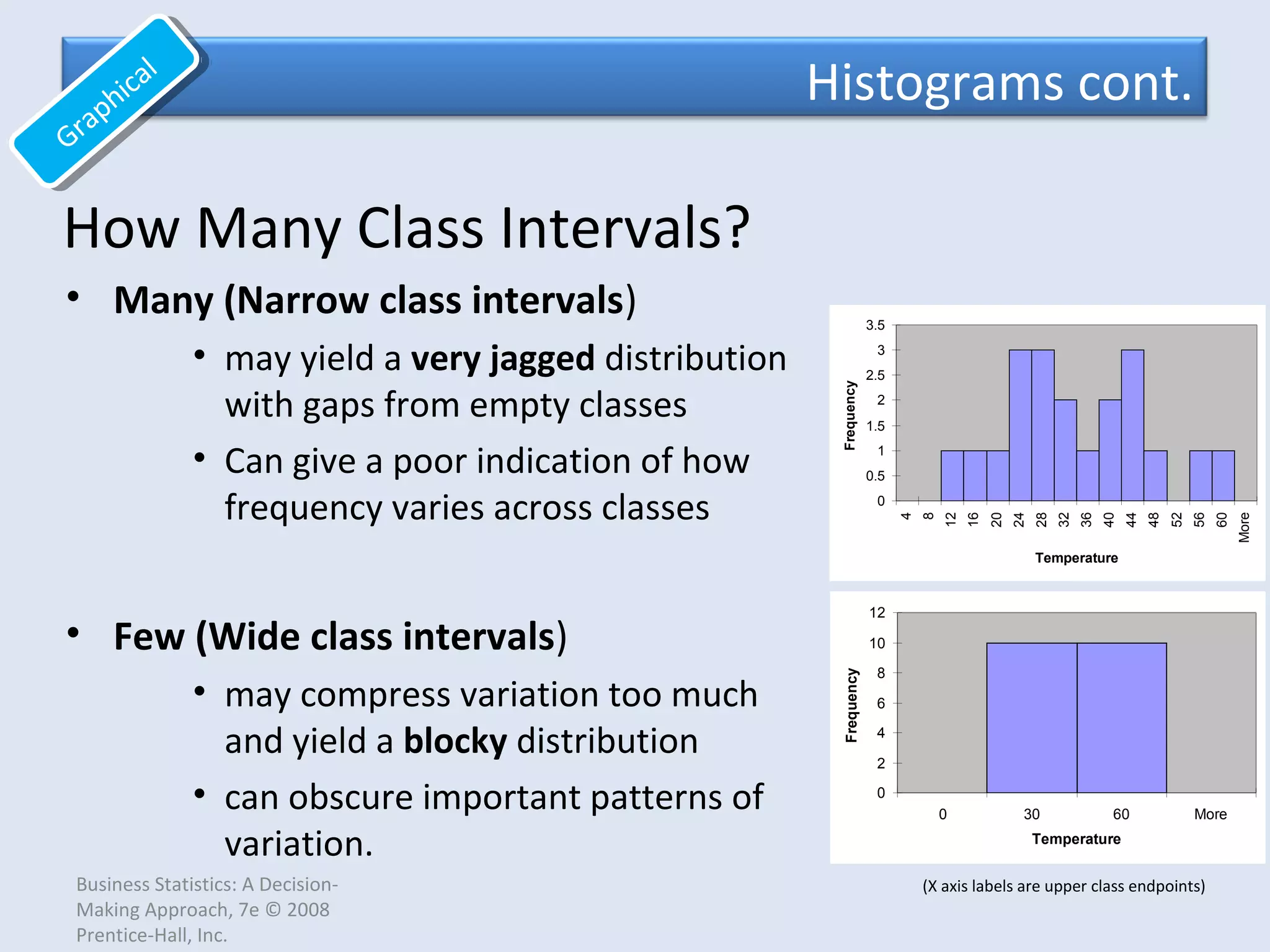
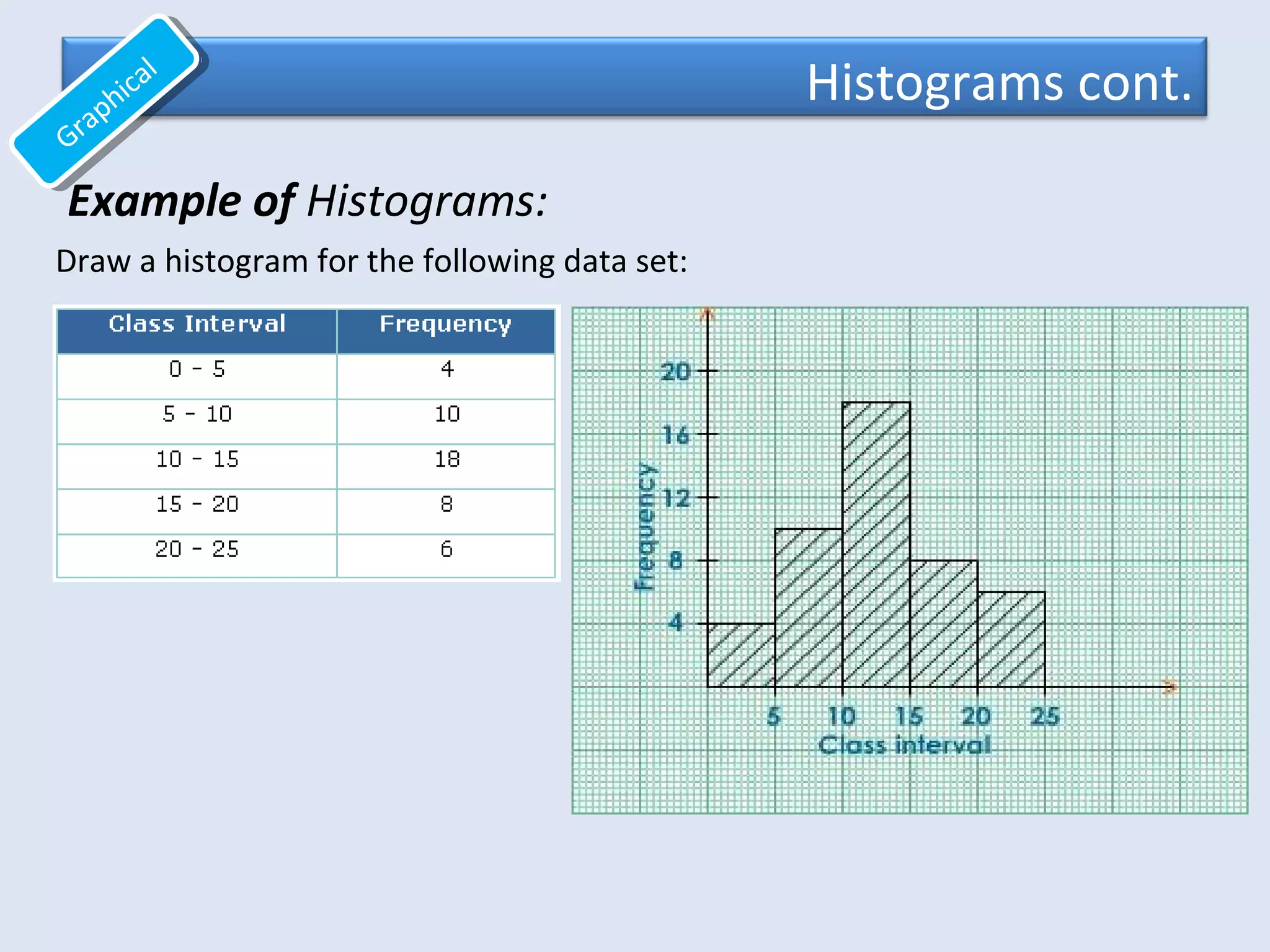
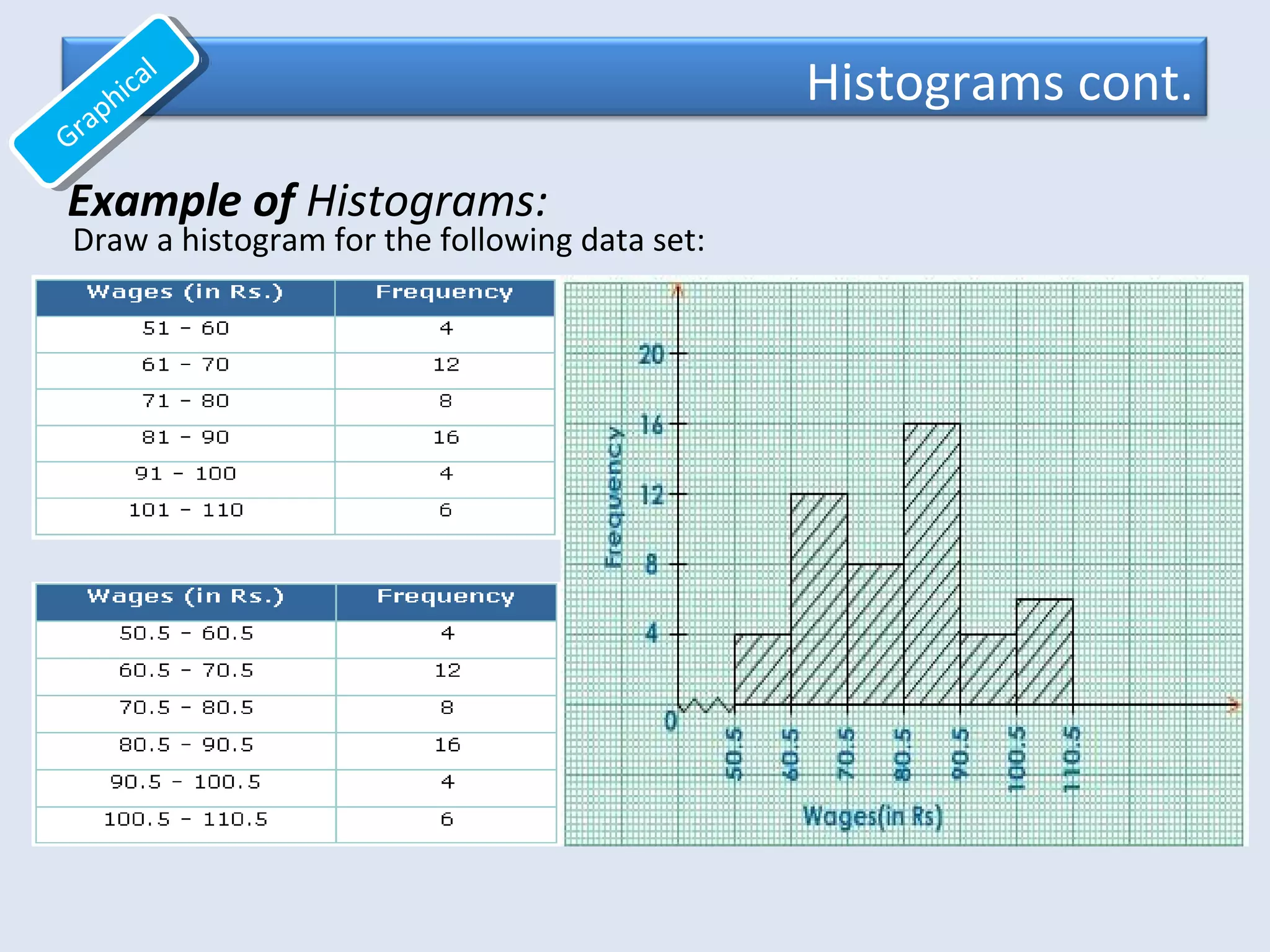
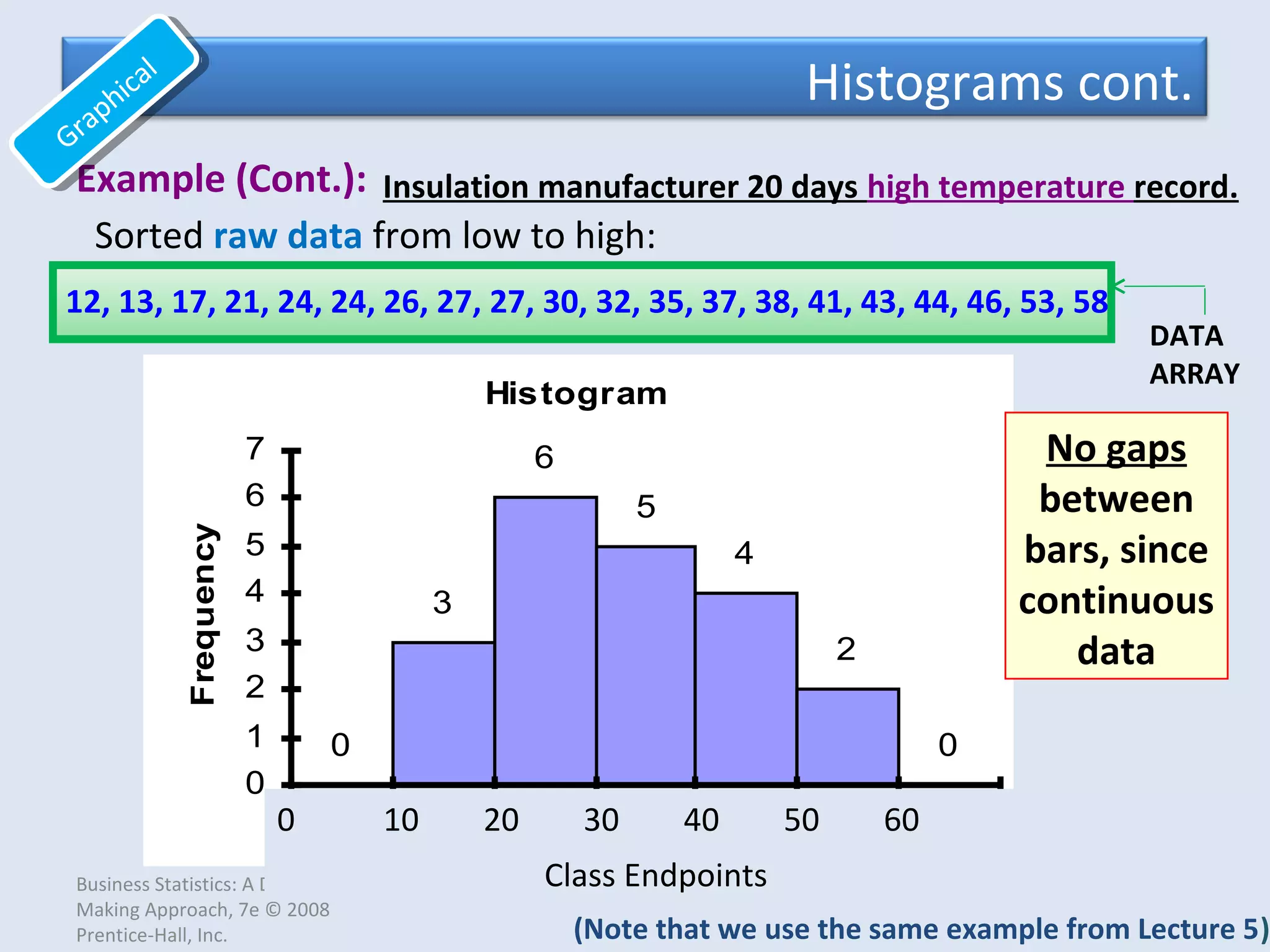
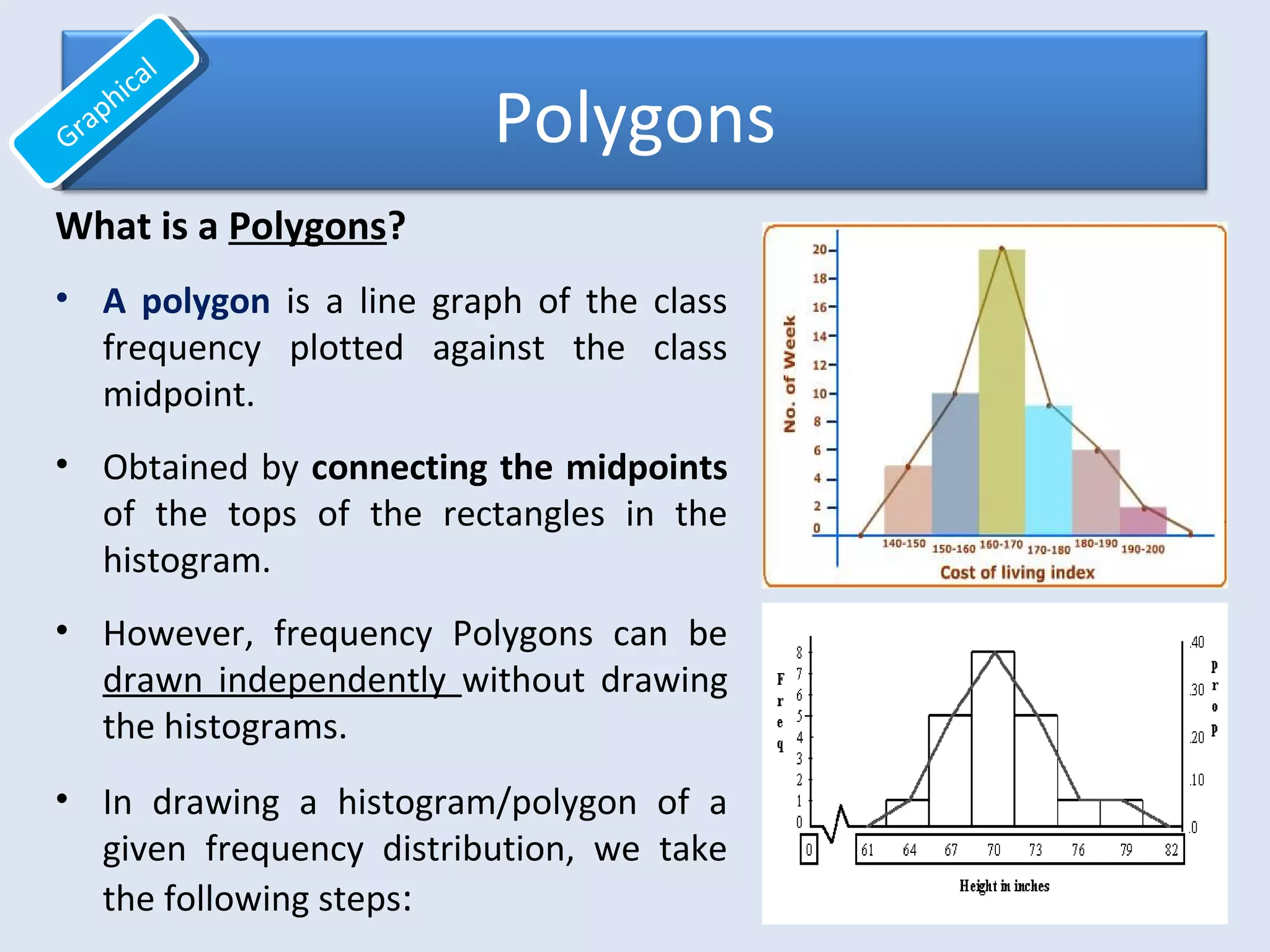
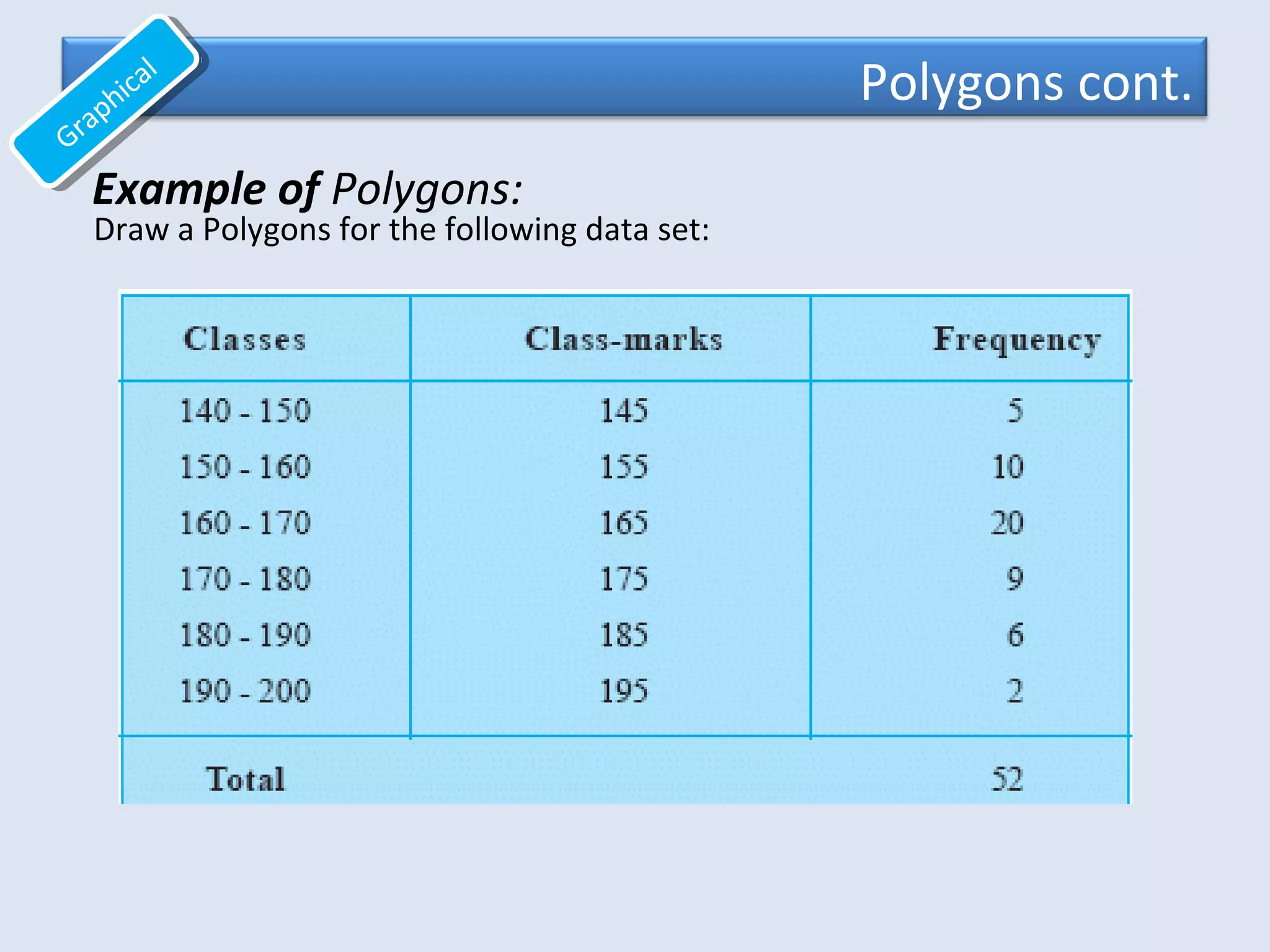
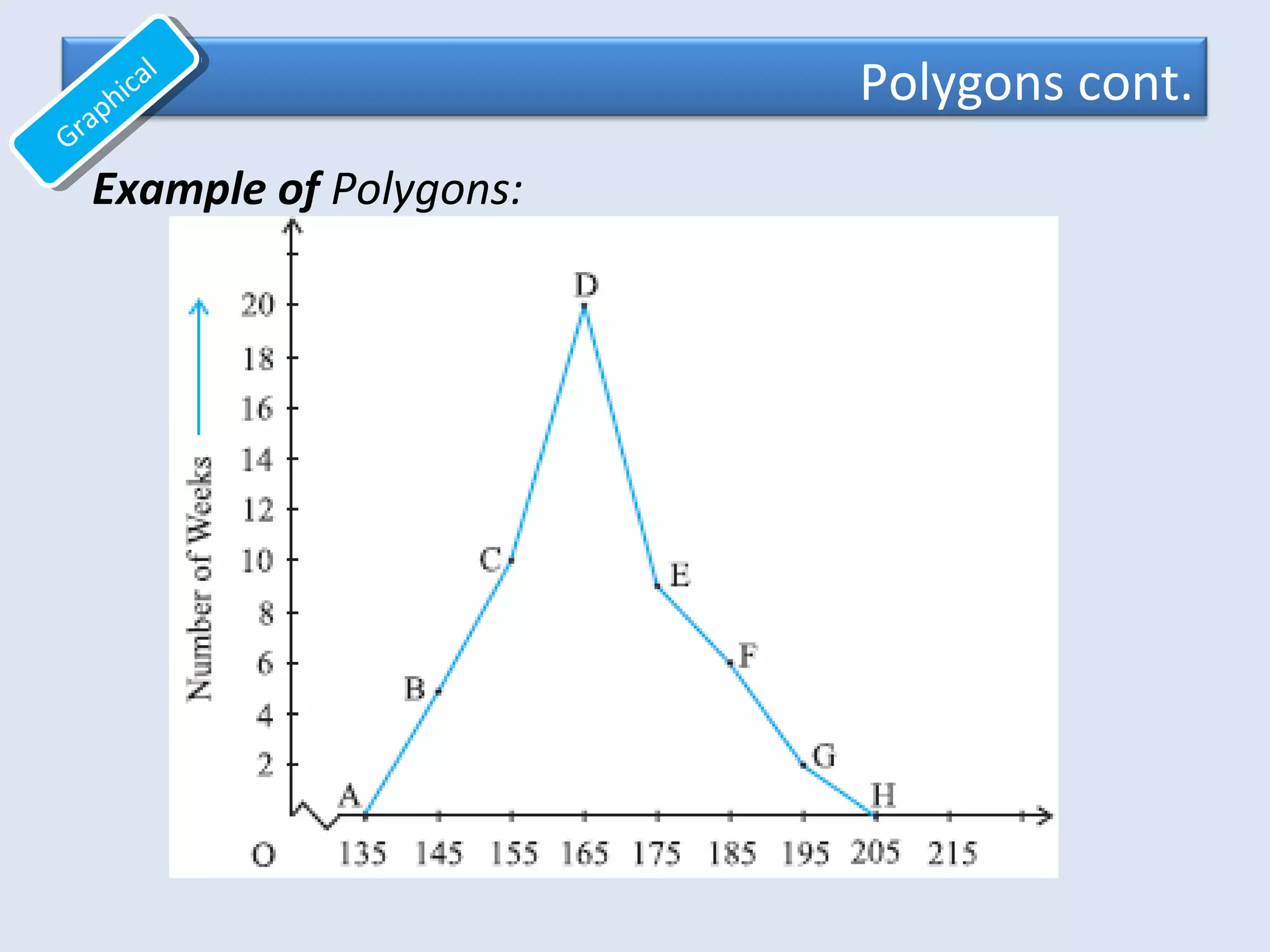
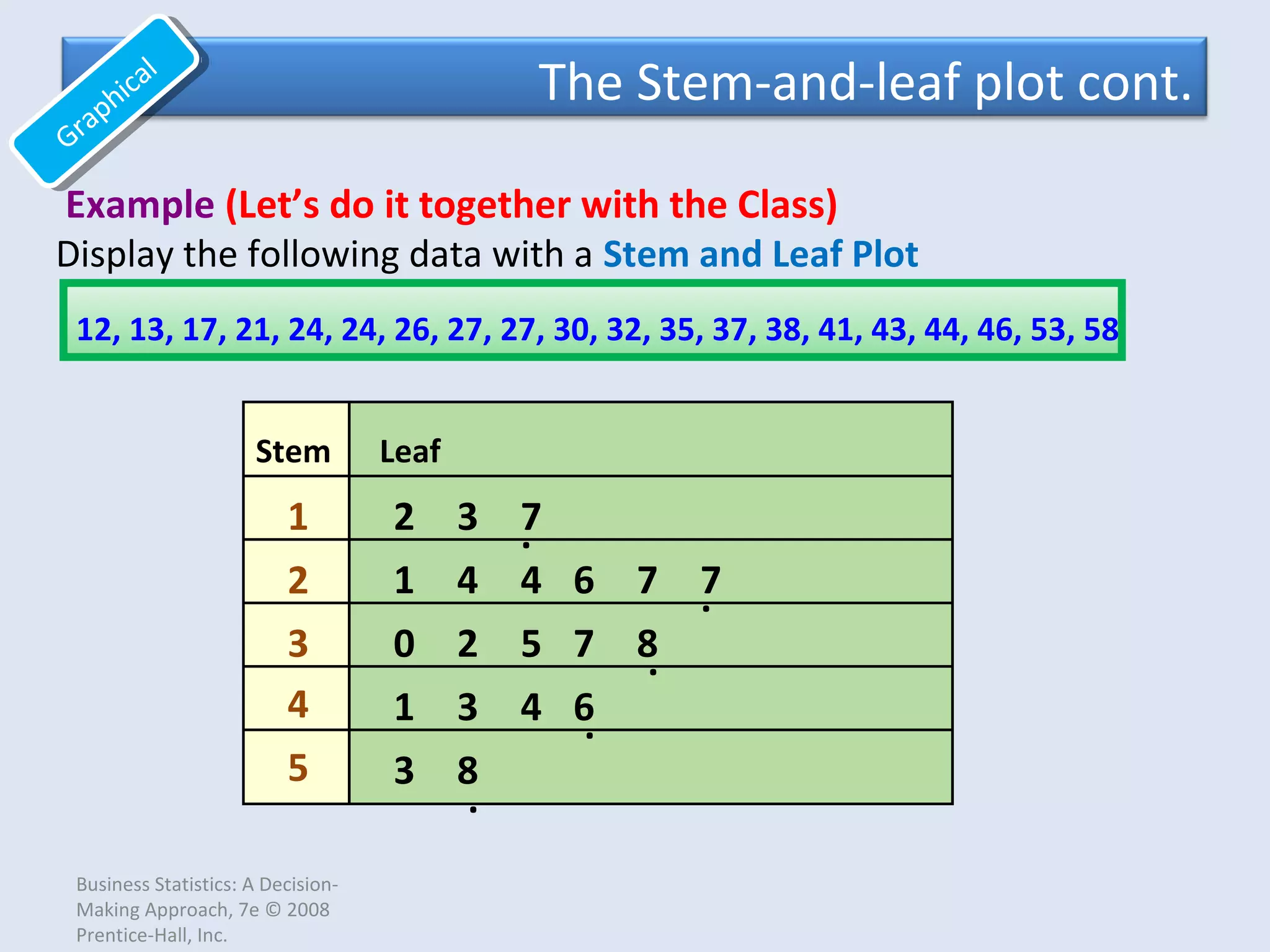
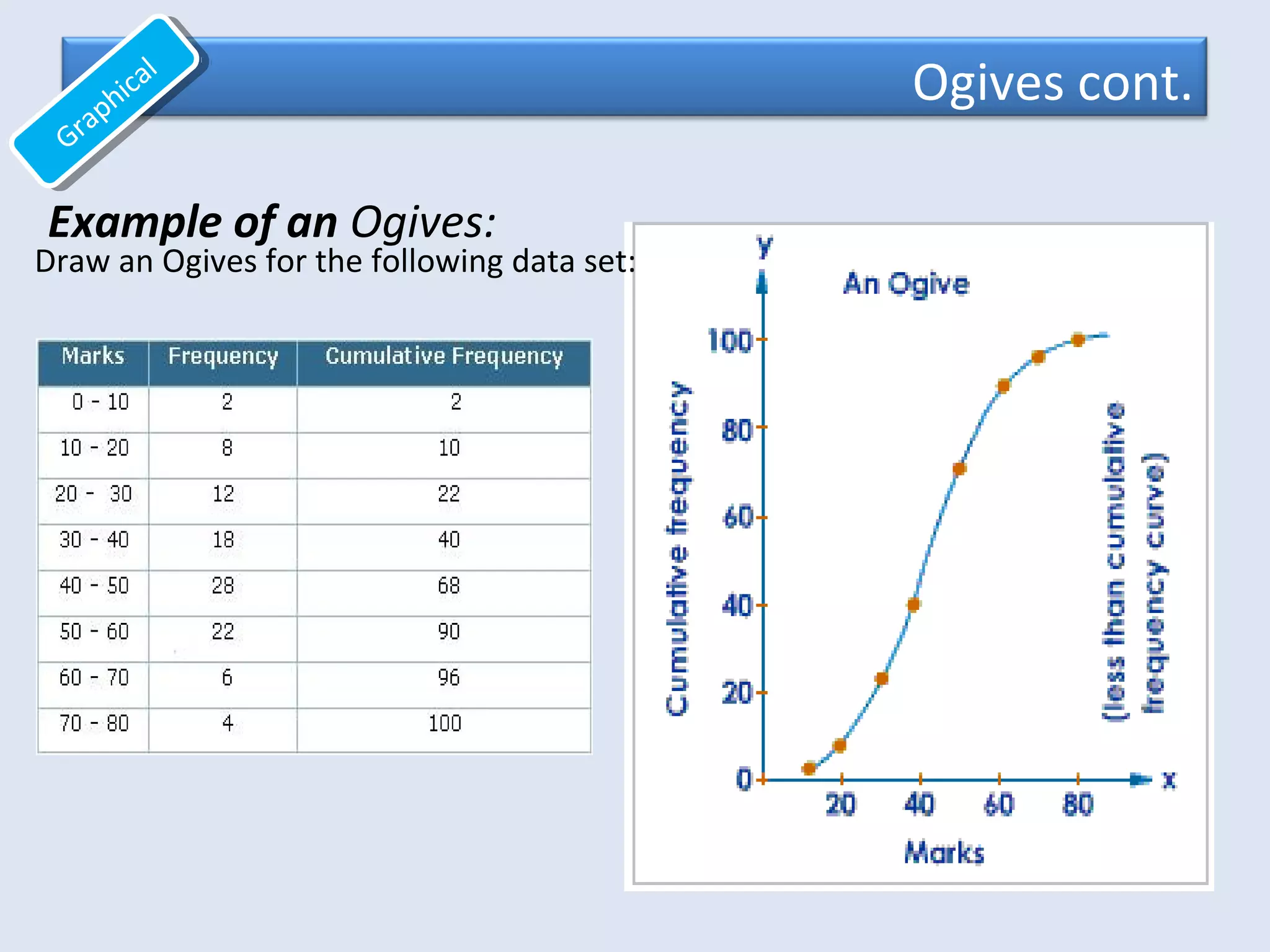
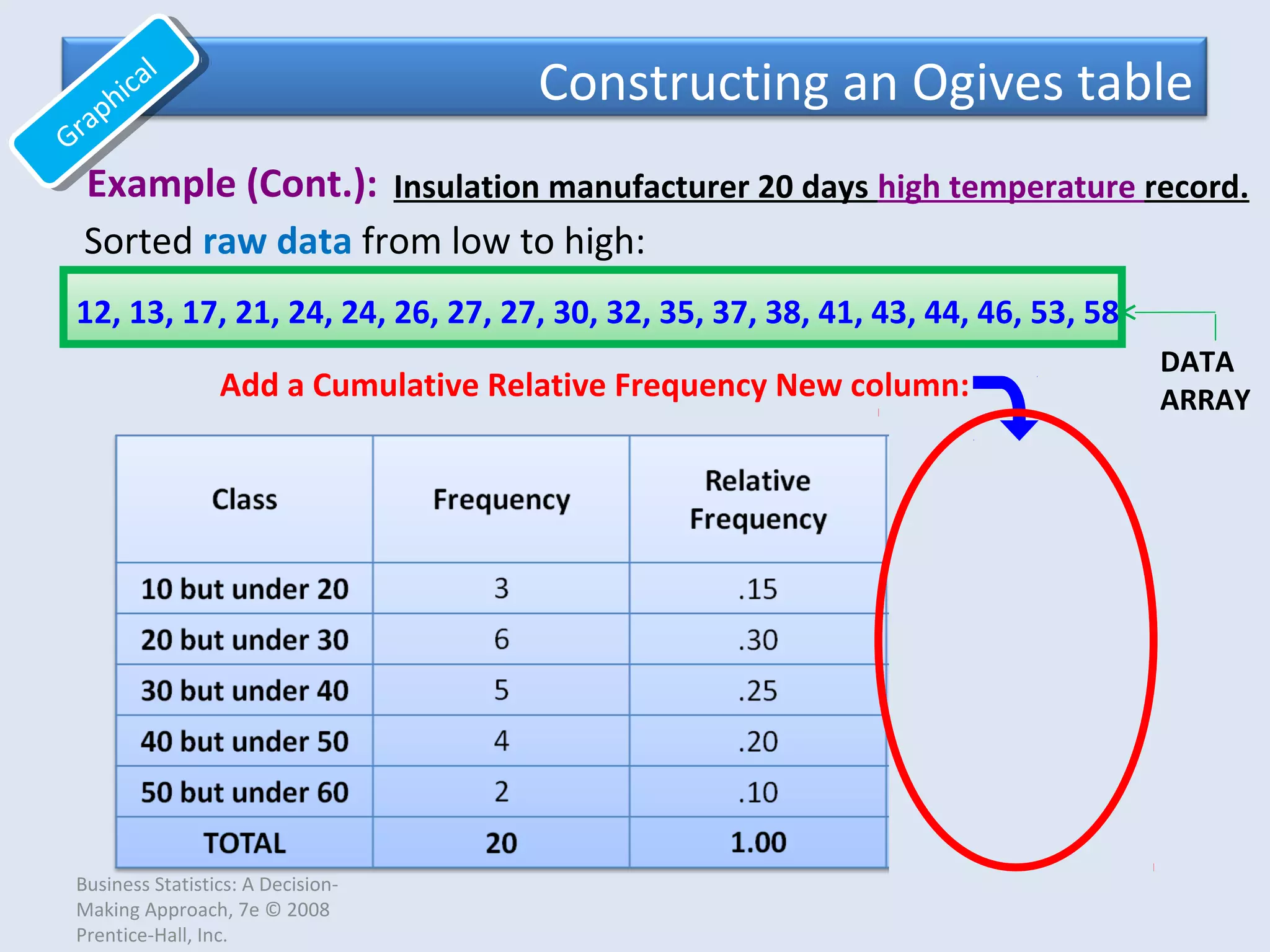
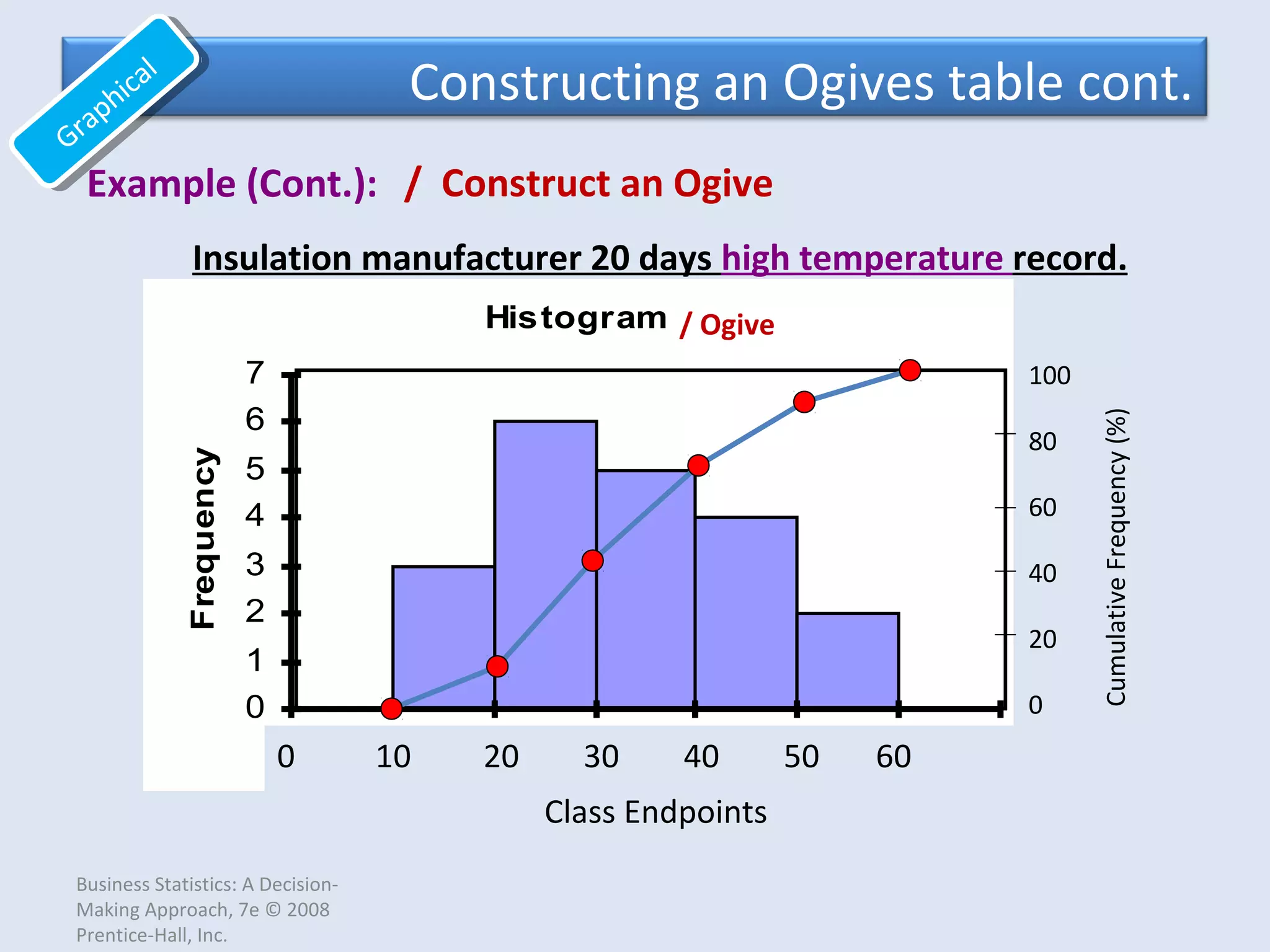
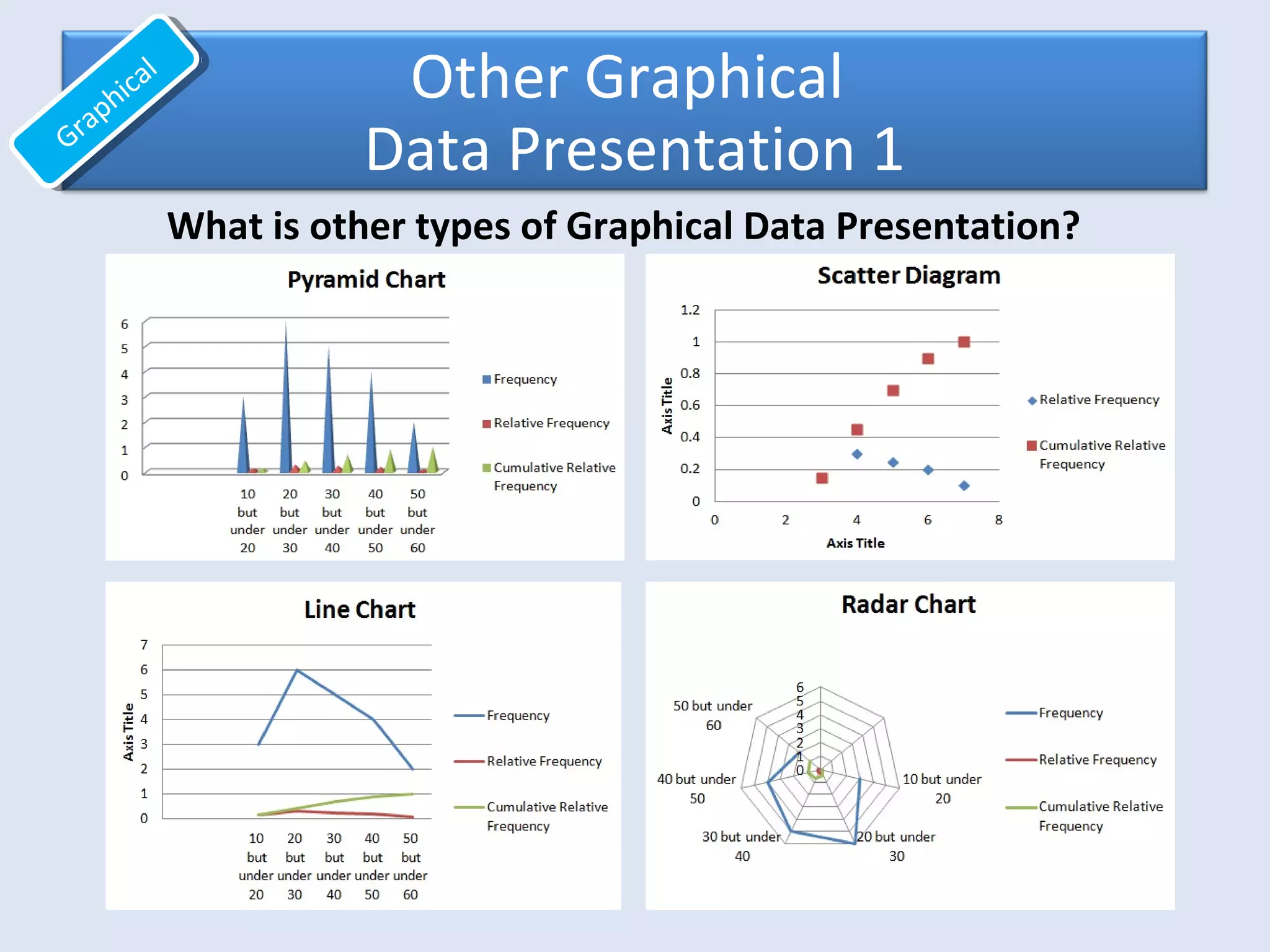
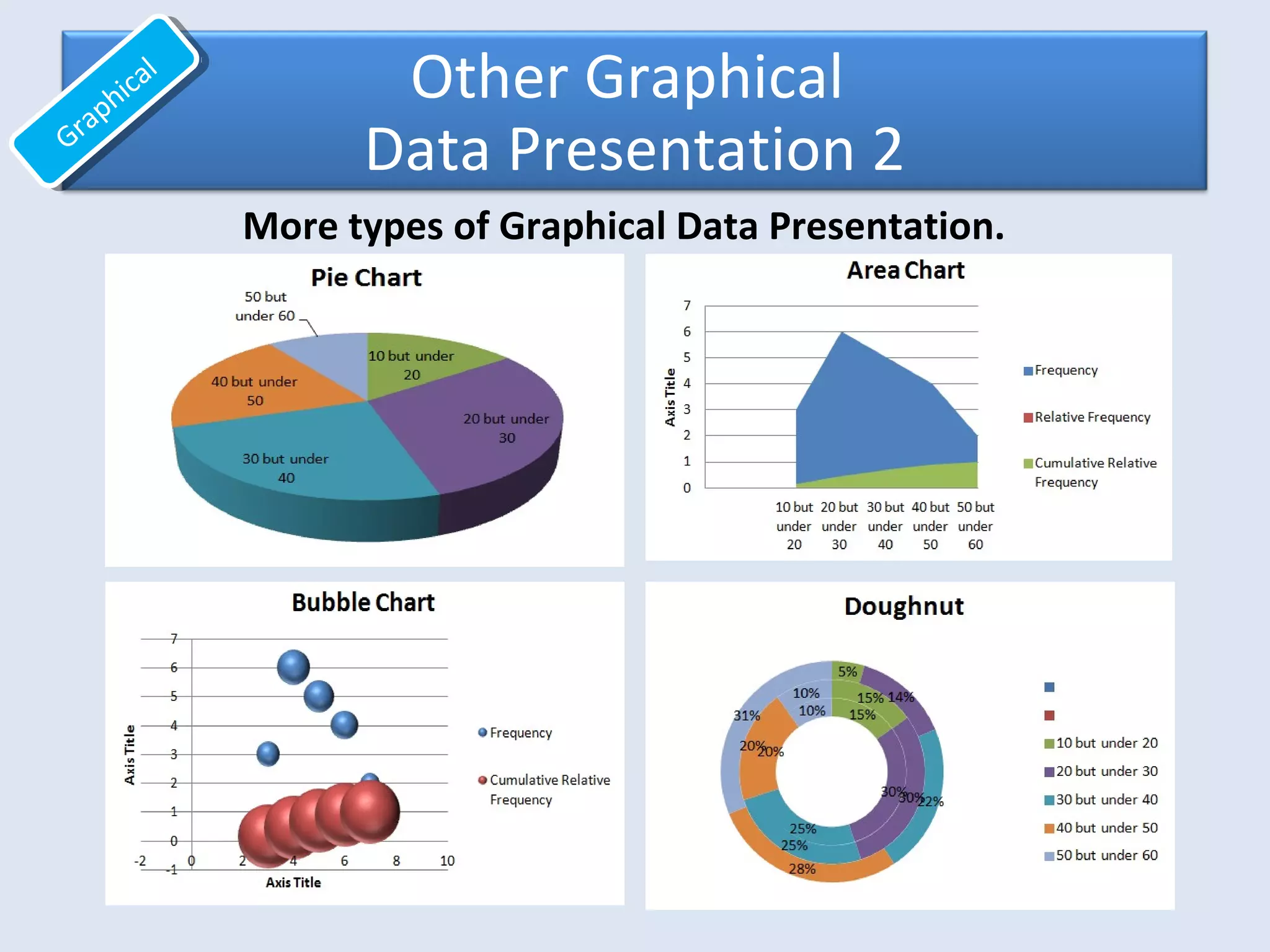
This document provides an overview of common quantitative data summarization techniques taught in a statistics course, including histograms, polygons, stem-and-leaf plots, and ogives. Histograms and polygons are used to graphically summarize frequency distributions through bar charts and line graphs. Stem-and-leaf plots organize raw data to show the shape of a distribution. Ogives graph cumulative relative frequencies to illustrate the proportion of data values below certain points. Examples are provided and steps are outlined for constructing each type of graphical summary.

1. Introduction to Statistics for Built
Environment
Course Code: AED 1222
Compiled by
DEPARTMENT OF ARCHITECTURE AND ENVIRONMENTAL DESIGN (AED)
CENTRE FOR FOUNDATION STUDIES (CFS)
INTERNATIONAL ISLAMIC UNIVERSITY MALAYSIA

2. Lecture 6
Summarizing Quantitative Data 2
Today’s Lecture:
 Summarizing Quantitative Data:
 Histograms & Polygons
 The Stem-and-Leaf plot
 Ogives

3. Contingency
Table
Contingency
Table
Data
Qualitative Quantitative
TabularTabular GraphicalGraphical TabularTabular GraphicalGraphical
Frequency
Distribution
Frequency
Distribution
Rel. Freq.
Dist.
Rel. Freq.
Dist.
Bar GraphBar Graph
Pie ChartPie Chart
Frequency
Distribution
Frequency
Distribution
Rel. Freq.
Dist.
Rel. Freq.
Dist.
Cumulative
Freq. Dist.
Cumulative
Freq. Dist.
Histograms
& Polygons
Histograms
& Polygons
Stem and
Leaf Plot
Stem and
Leaf Plot
An overview
OgivesOgives
LECTURE
5
An overview of common data presentation:
LECTURE
4

4. Histograms
What is a Histograms?
• The histogram is a summary graph showing a count of the
data points falling in various ranges.
• The groups of data are called classes, and in the context of a
histogram they are known as bins, because we can think of
them as containers that accumulate data and "fill up" at a
rate equal to the frequency of that data class
• Consists of a set of rectangles
• Bases at X axis,
• Centers at the midpoints,
• Lengths equals to the class interval size,
• Areas proportional to the class frequencies.
Graphical
Graphical

5. Histograms cont.
• Unlike a bar graph, a histogram has no natural separation or
gap between rectangles of adjacent classes.
• The class boundaries are marked on the horizontal axis (X
Axis) and the frequency is marked on the vertical axis (Y
Axis). Thus a rectangle is constructed on each class interval.
• If the intervals are equal, then the height of each rectangle
is proportional to the corresponding class frequency.
• If the intervals are unequal, then the area of each rectangle
is proportional to the corresponding frequency density.
Graphical
Graphical

6. Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
How Many Class Intervals?
• Many (Narrow class intervals)
• may yield a very jagged distribution
with gaps from empty classes
• Can give a poor indication of how
frequency varies across classes
• Few (Wide class intervals)
• may compress variation too much
and yield a blocky distribution
• can obscure important patterns of
variation.
0
2
4
6
8
10
12
0 30 60 More
Temperature
Frequency
0
0.5
1
1.5
2
2.5
3
3.5
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
More
Temperature
Frequency
(X axis labels are upper class endpoints)
Histograms cont.
Graphical
Graphical

7. Histograms cont.
Draw a histogram for the following data set:
Example of Histograms:
Graphical
Graphical

8. Histograms cont.
Graphical
Graphical
Draw a histogram for the following data set:
Example of Histograms:

9. Distribution of shops according to the number of wage
- earners employed at a shopping complex
When the intervals are unequal, we construct each rectangle
with the class intervals as base and frequency density as height.
Frequency Density
Histograms cont.
Graphical
Graphical
Draw a histogram for the following data set:
Example of Histograms:

10. Histograms cont.
Graphical
Graphical
Distribution of shops according to the number of wage
- earners employed at a shopping complex

11. Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
Histogram
0
3
6
5
4
2
0
0
1
2
3
4
5
6
7
5 15 25 36 45 55 More
Frequency
Class Midpoints
0 10 20 30 40 50 60
Class Endpoints
Example (Cont.):
DATA
ARRAY
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
Sorted raw data from low to high:
Insulation manufacturer 20 days high temperature record.
Histograms cont.
Graphical
Graphical
No gaps
between
bars, since
continuous
data
(Note that we use the same example from Lecture 5)

12. Information conveyed
by Histograms
Why use Histograms?
-Histograms are useful data summaries that convey the
following information:
• The general shape of the frequency distribution
• Symmetry of the distribution and whether it is
skewed
• Modality: unimodal, bimodal, or multimodal
Graphical
Graphical
-A histogram may become more appropriate as the data
size increases.
-The ease with which histograms can now be generated
on computers.

13. Comparison between
Histograms & Bar GraphsGraphical
Graphical

14. Polygons
What is a Polygons?
• A polygon is a line graph of the class
frequency plotted against the class
midpoint.
• Obtained by connecting the midpoints
of the tops of the rectangles in the
histogram.
• However, frequency Polygons can be
drawn independently without drawing
the histograms.
• In drawing a histogram/polygon of a
given frequency distribution, we take
the following steps:
Graphical
Graphical

15. Polygons cont.
Graphical
Graphical
Step 1. : If the frequency table is in the inclusive form, we first
convert it into an exclusive form and make it a continuous
interval.
Step 2. :To complete the polygon we assume a class interval
with zero frequency preceding the first class interval and a
class interval with zero frequency succeeding the last class
interval.
Step 3. : Taking a suitable scale, we represent the class mid-
points or (class marks) along X axis.
Step 4. : Taking a suitable scale, we represent frequency along
Y axis.
Step 5. : We plot the corresponding points and join it with the
help of line segment.
Procedure

16. Polygons cont.
Example of Polygons:
Graphical
Graphical
Draw a Polygons for the following data set:

17. Polygons cont.
Example of Polygons:
Graphical
Graphical

18. The Stem-and-Leaf plot
What is a Stem-and-Leaf Plot?
• The Stem-and-leaf plot is a device for presenting quantitative
data in a graphical format, similar to a histogram, to assist in
visualizing the shape of a distribution.
• Unlike histograms, stemplots retain the original data.
• A basic stemplot contains two columns separated by a vertical
line. The left column contains the stems and the right column
contains the leaves.
• Consists of a set of a : Stem: Leading Digits
Leaf: Trailing digits
Graphical
Graphical

19. Step 1. : Separate the sorted data series into leading digits
(the stem) and the trailing digits (the leaves).
Step 2. : List all stems in a column from low to high.
Step 3. : For each stem, list all associated leaves.
Procedure
The Stem-and-leaf plot cont.
Graphical
Graphical

20. Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
• Here, use the 10’s digit for the stem unit:
Data sorted from low to high:
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
 12 is shown as
 35 is shown as
Stem Leaf
The Stem-and-leaf plot cont.
Graphical
Graphical
1 2
3 5

21. Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
Using other stem units
– Round off the 10’s digit to form the leaves
The Stem-and-leaf plot cont.
Graphical
Graphical
• Here, use the 100’s digit for the stem unit:
 613 would become
 776 would become
 1224 would become
Stem Leaf
6 1
12 2
7 8

22. Example (Let’s do it together with the Class)
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
Display the following data with a Stem and Leaf Plot
The Stem-and-leaf plot cont.
Graphical
Graphical
Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
4
5
2
1
0
1
3
3
1
2
Stem Leaf
3 7
4 4
2 5
3 4
6 7
7 8
6
8
7
.
.
.
.
.

23. Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
Why use Stem-and-Leaf Plot?
• A simple way to see distribution details from
quantitative data
The Stem-and-leaf plot cont.
Graphical
Graphical
• Stemplots are useful for giving the reader a quick
overview of distribution, highlighting outliers and
finding the mode.

24. Ogives
What is an Ogives?
• An Ogive is a graph of the cumulative relative frequencies
from a relative frequency distribution.
• Ogives are sometime shown in the same graph as a relative
frequency histogram.
• Also known as Cumulative Frequencies Graph.
Graphical
Graphical
Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.

25. Example of an Ogives:
Draw an Ogives for the following data set:
Ogives cont.
Graphical
Graphical

26. Example (Cont.):
DATA
ARRAY
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
Constructing an Ogives table
Sorted raw data from low to high:
Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
Add a Cumulative Relative Frequency New column:
Graphical
Graphical
Insulation manufacturer 20 days high temperature record.

27. Example (Cont.):
Constructing an Ogives table cont.
Business Statistics: A Decision-
Making Approach, 7e © 2008
Prentice-Hall, Inc.
Graphical
Graphical
Histogram
0
1
2
3
4
5
6
7
5 15 25 36 45 55 More
Frequency
Class Midpoints
100
80
60
40
20
0
CumulativeFrequency(%)
/ Ogive
0 10 20 30 40 50 60
Class Endpoints
Insulation manufacturer 20 days high temperature record.
/ Construct an Ogive

28. PYRAMID
CHART
LINE CHART
SCATTER
DIAGRAM
RADAR CHART
Other Graphical
Data Presentation 1
What is other types of Graphical Data Presentation?
Graphical
Graphical

29. PIE CHART
BUBBLE CHART
AREA CHART
DOUGHNUT
Other Graphical
Data Presentation 2
More types of Graphical Data Presentation.
Graphical
Graphical