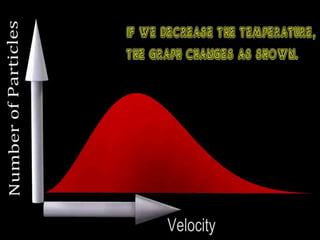
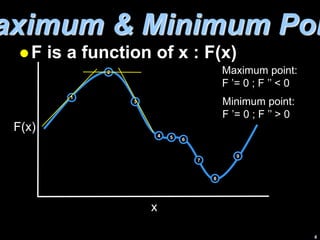
This document discusses the distribution of energy states in a system of molecules. It introduces concepts like: 1) A system's total energy is constant, while individual molecules can have different energy levels. The distribution of molecules among different energy states will dominate the overall configuration. 2) The dominating configuration is the one that maximizes the function W, which represents the probability of a given distribution of molecules among energy states. 3) Finding the maximum of W involves taking its derivative and applying constraints like constant total energy and number of molecules. This leads to an equation that can determine the most probable distribution of states.

1. 1
Assembly
of Systems
N, E, T, P, V,
m, etc.
Environment

2. 2
Energy of a System
 Energy of a macroscopic system is
𝐸 =
𝒊
𝑬𝑖𝒏𝑖
 Energy of a microscopic system is Ei
 A macroscopic system consists of
countless microscopic systems
𝑵 =
𝒊
𝒏𝑖

3. The Distribution of Molecular States
 A system composed of N molecules
 Total energy (E) is constant (Equilibrium)
 Posible energy state for each molecule (ei)
 Molecules are in different states (i) and possess
different energy levels Ej
 Total energy E = Ej = (ei ni)
 Ej is fluctuated due to molecular collision
 Constraint: Ej = E
 The distribution of energy is the population of a
state (there are ni molecules in ei energy level)
 {0,1,5,7,1,0}
3

4. 4

5. 5
The Dominating Configuration
 Some specific configuration have much greater weights than others
 There is a configuration with so great a weight that it overwhelms all
the rest
 W is a function of all ni: W(n0, n1, n2 …)
 The dominating configuration has the values of ni that lead to a
maximum value of W
 The number of molecule constraint :
 The energy constraint :
E
n
i
i
i 
 e
N
n
i
i 


6. 6
aximum & Minimum Poi
 F is a function of x : F(x)
Maximum point:
F ’= 0 ; F ’’ < 0
Minimum point:
F ’= 0 ; F ’’ > 0
1
2
3
4 5 6
7
8
9
F(x)
x

7. 7
Maximum Value of W{ni}
 We are looking for the best set
of ni that yields maximum value
of ln(W)
Maximum W = W{ni,max}
Maximum ln W = ln W{ni,max}
{ni,max} = ?

8. 8
Maximum Value of W{ni }
 {ni,max} can be determined by
differentiate
 Constraints
Total particle (N) is constant
Total energy (E) is constant
0
ln
ln 










 
i
i
i
dn
n
W
W
d


i
i
in
E e 0

 
i
i
idn
dE e


i
i
n
N 0

 
i
i
dn
dN

9. 9
Maximum Value of W{ni
 Maximum ln(W) plus Constraints
 Method of undetermined multipliers
0
ln
ln 










 
i
i
i
dn
n
W
W
d
0


i
i
idn
e
0


i
i
dn



































i
i
i
i
i
i
i
i
i
i
i
i
dn
n
W
dn
dn
dn
n
W
e

e


ln
ln

10. 10
aximum & Minimum in 3
F(x,y)