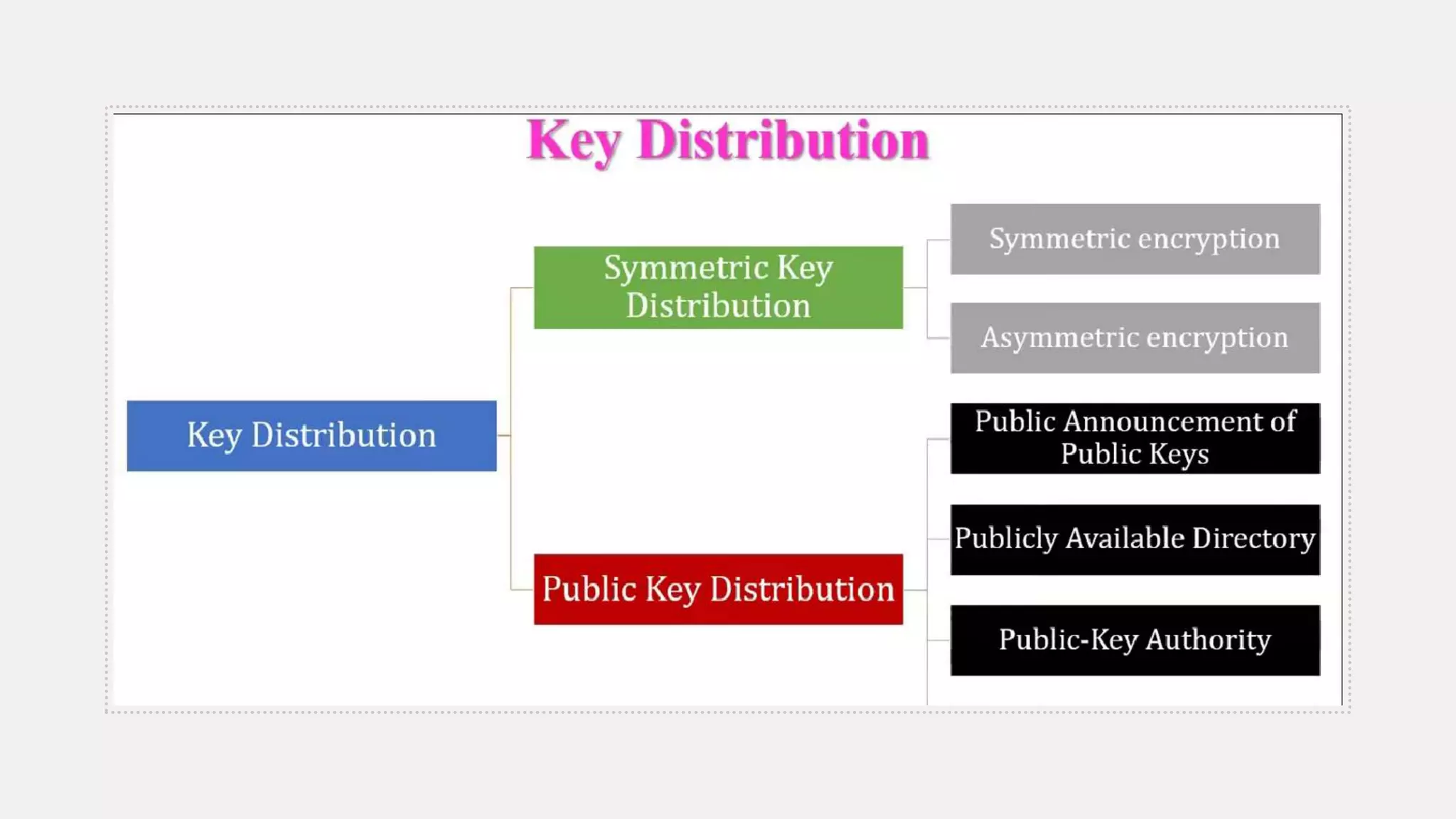
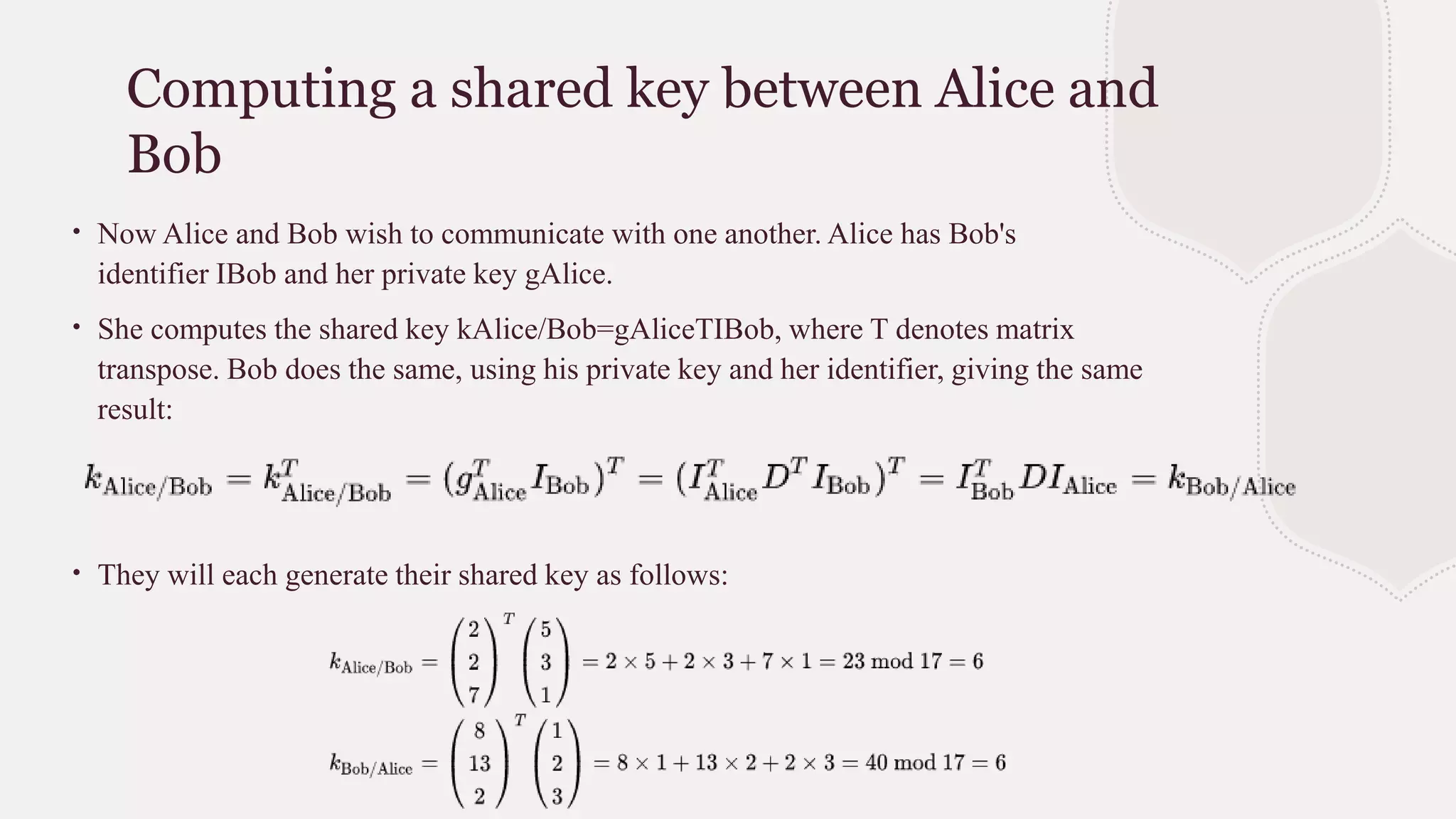
Blom's key pre-distribution scheme is a symmetric threshold key exchange protocol that allows any two participants who receive a secret key from a trusted party to independently create a shared key for secure communication. The trusted party chooses a random secret matrix and uses it to compute private keys for each new participant based on their public identifier. Any two participants can then use their private key and the other's public identifier to compute the same shared key. The scheme provides security as long as fewer than k private keys are compromised, since k linearly independent identifiers are needed to compute other keys.

1. Blom’s Key
Pre-distribution Scheme
- J A Y E S H
S U K D E O P A T I L

2. What is Key Pre-Distribution
∙ Key Pre-distribution is a scheme to distribute keys onto different sensor nodes
prior to deployment. Therefore, these sensor nodes creates network through
establishing secured links between different nodes using their shared secret keys
after the deployment.
∙ A key pre-distribution scheme has three phases:
∙ 1) Key Distribution
∙ 2) Shared Key Discovery
∙ 3) Path-key establishment.

4. Blom’s Key Pre-distribution Scheme
∙ Blom's scheme is a symmetric threshold key exchange protocol in cryptography. The scheme
was proposed by the Swedish cryptographer Rolf Blom in a series of articles in the early
1980s.
∙ A trusted party gives each participant a secret key and a public identifier, which enables any
two participants to independently create a shared key for communicating. Every participant
can create a shared key with any other participant, allowing secure communication
to take place between any two members of the group.However, if an attacker can
compromise the keys of at least k users, they can break the scheme and reconstruct every
shared key. Blom's scheme is a form of threshold secret sharing.
∙ Blom's scheme is currently used by the HDCP (High-bandwidth Digital Content
Protection) copy protection scheme to generate shared keys for high-definition content
sources and receivers, such as HD DVD players and high-definition televisions.

5. ∙ The protocol
The key exchange protocol involves a
trusted party (Trent) and a group
of n users. Let Alice and Bob be two
users of the group.

6. ∙ Protocol setup
Trent chooses a random and secret symmetric
matrix Dk,k over the finite field GF(p), where p is a
prime number. D is required when a new user is to be
added to the key sharing group.

7. ∙ Inserting a new participant
New users Alice and Bob want to join the key exchanging group. Trent chooses public
identifiers for each of them; i.e., k-element vectors:
∙ For example:
∙ Trent then computes their private keys:

8. ∙ Using D as described above:
Each will use their private key to compute shared keys with other participants of
the group

9. Computing a shared key between Alice and
Bob
∙ Now Alice and Bob wish to communicate with one another. Alice has Bob's
identifier IBob and her private key gAlice.
∙ She computes the shared key kAlice/Bob=gAliceTIBob, where T denotes matrix
transpose. Bob does the same, using his private key and her identifier, giving the same
result:
∙ They will each generate their shared key as follows:

10. Attack resistance
∙ In order to ensure at least k keys must be compromised before every shared
key can be computed by an attacker, identifiers must be k-linearly
independent: all sets of k randomly selected user identifiers must be linearly
independent.
∙ Otherwise, a group of malicious users can compute the key of any other
member whose identifier is linearly dependent to theirs. To ensure this
property, the identifiers shall be preferably chosen from a MDS-Code matrix
(maximum distance separable error correction code matrix).
∙ The rows of the MDS-Matrix would be the identifiers of the users. A MDS-
Code matrix can be chosen in practice using the code-matrix of the Reed–
Solomon error correction code (this error correction code requires only easily
understandable mathematics and can be computed extremely quickly).

11. References:
∙ https://weekly-geekly.imtqy.com/articles/269229/index.html
∙ http://cgiold.di.uoa.gr/~halatsis/Crypto/Bibliografia/Crypto_Lectures/Stin
son_lectures/lec09.pdf
∙ https://mjoc.uitm.edu.my/main/images/journal/vol6-2-2021/3-Udin-et-al-
Vol-62.pdf