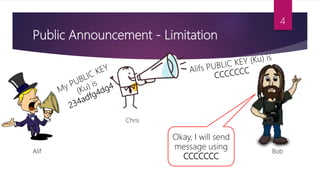
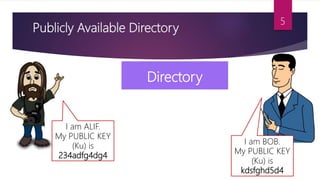
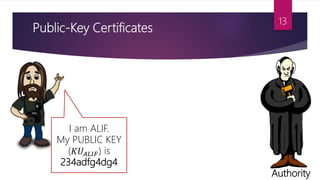
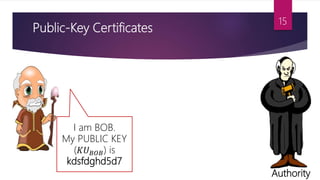
This document discusses key management techniques including public key distribution methods like public announcement, publicly available directories, public-key authorities, and public-key certificates. It also explains Diffie-Hellman key exchange, which allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure communications channel.