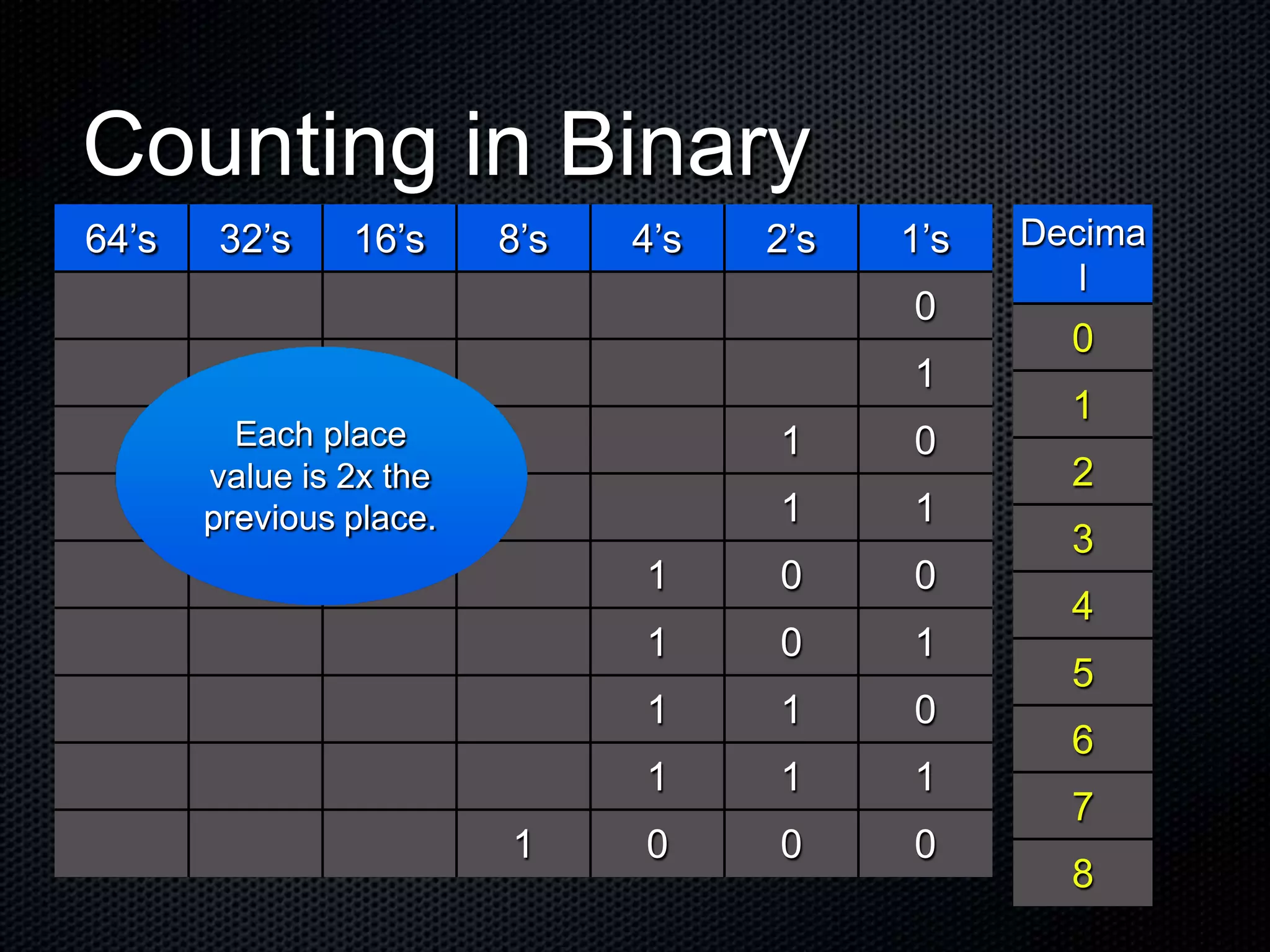
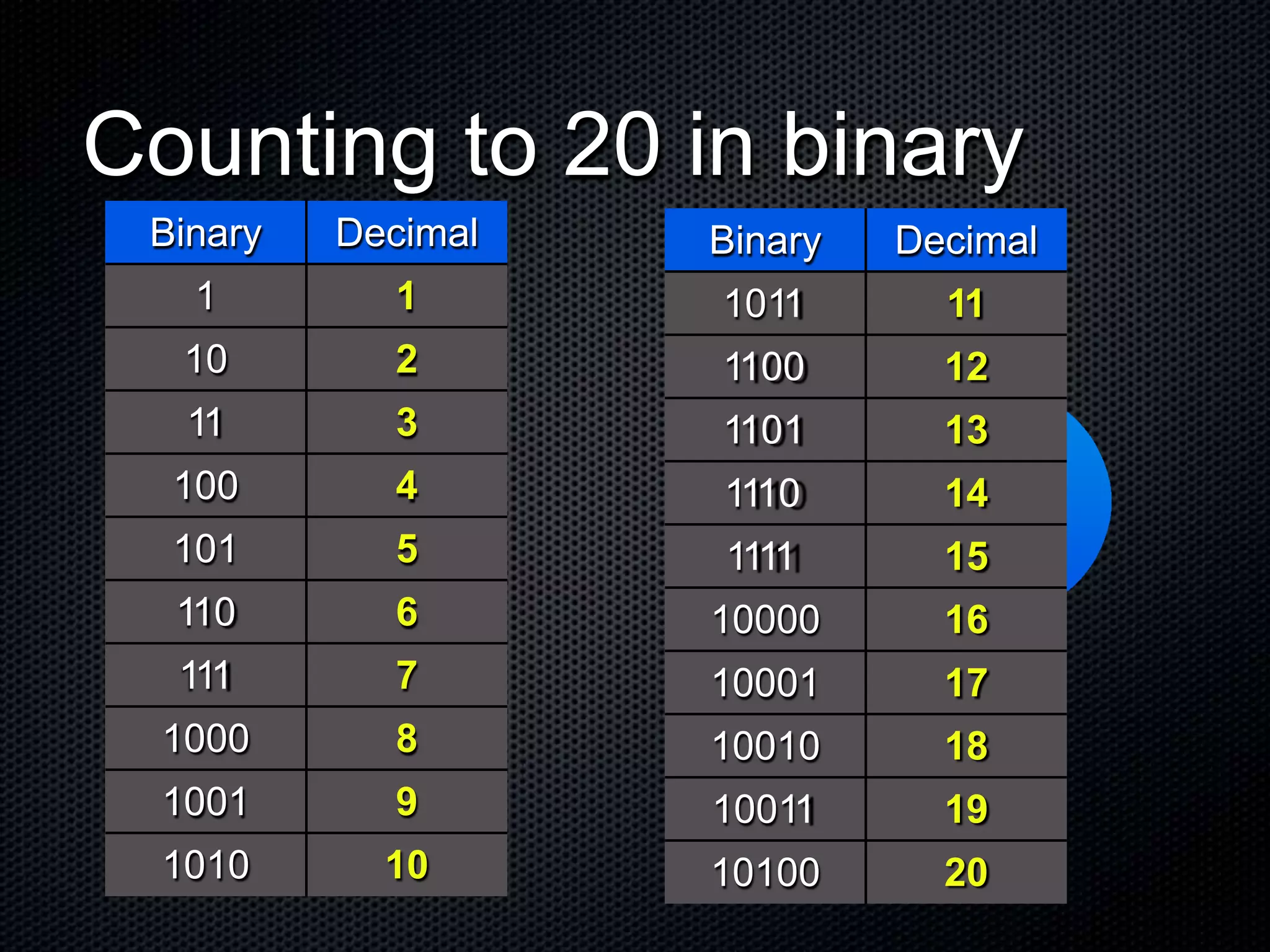
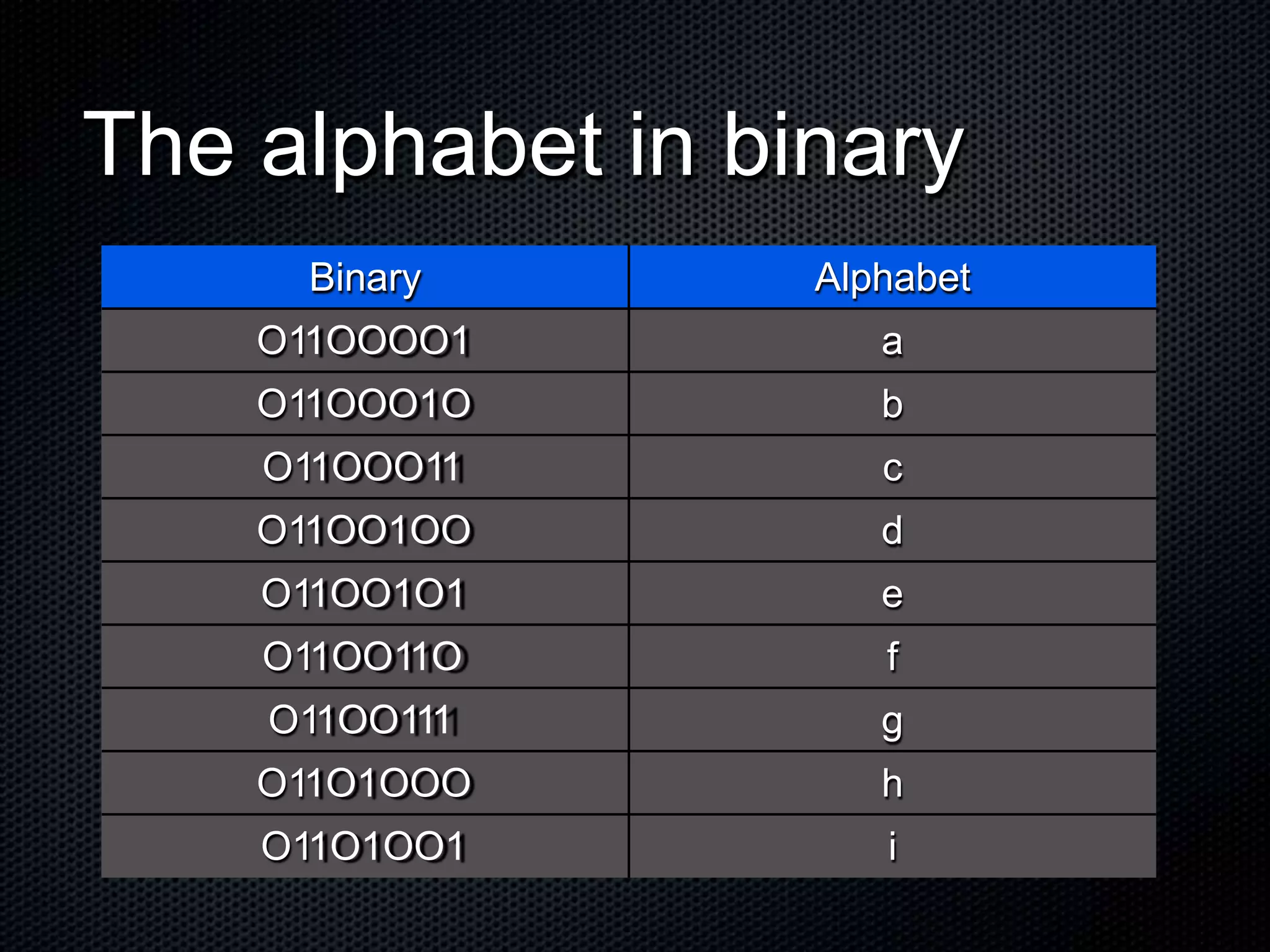
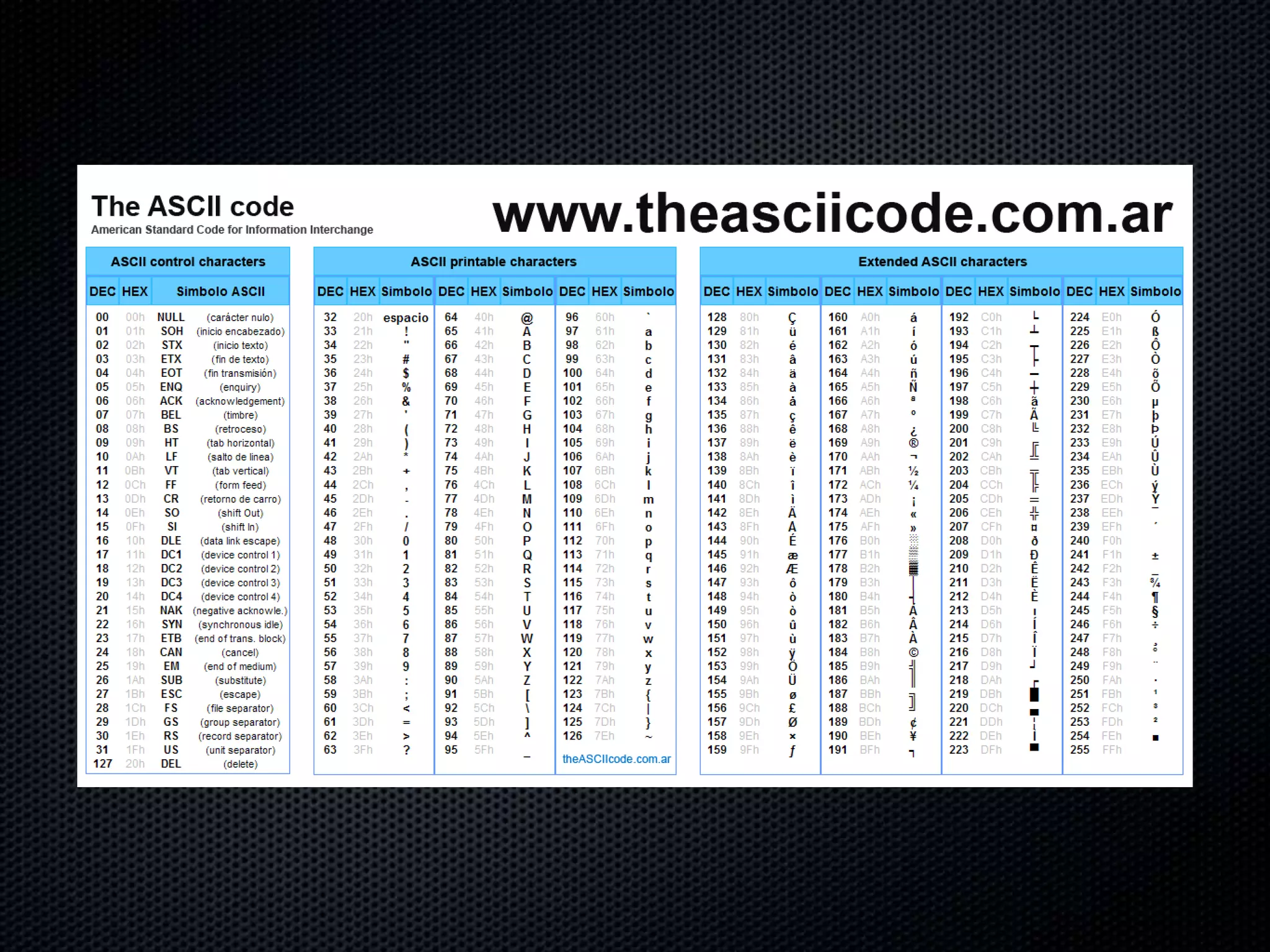
Binary code represents all data and instructions inside a computer using only the digits 0 and 1. It works by using place values that double in value at each place, from right to left, similar to our decimal system which uses place values that are 10 times greater at each place. Bytes, which are made up of 8 bits, can represent a single character by assigning a unique 8-bit binary number to each letter, number, and symbol. Understanding binary code is essential for learning computer programming and how computers work at a fundamental level.

1. Binary Code
The Language of Your Computer

2. Input/Output
Input is whatever is put into a computer.
Input can be data, letters, numbers, symbols, shapes,
sounds, pressure, light beams or whatever material
needs processing.
Output hardware consists of devices that translate
information processed by the computer into a form
humans can understand - print, sound, graphics, or
video, for example.

3. The Binary System
The base of all programs is the binary
number system of two - 1 and 0.
system, a
These represent On and Off - the position for an
electrical signal to pass through (or not) a transistor.
All data and
computer to
represented
program instructions that go into the
be processed and stored, are
by these binary numbers.

4. Decimal System
To understand the binary system,
our Base 10, decimal system.
The prefix “dec-” means 10
we need to review
Our decimal system is based on
(0,1,2,3,4,5,6,7,8,9)
10 numbers
When counting, using place value, we fill the ones
place and then move to the tens place.

5. For example:
When you count in the
decimal system (base 10)
you fill the one’s place, then
move to the ten’s place.
Only the numbers 0 - 9 are
used.
As each place value is filled
with the numbers, we
continue to the next place
value. Each place value is
10x the previous place.
100’s 10’s 1’s
9 9
1 0 0
1 0 1
10’s 1’s
9
1 0
1 1
1 2
1 3

6. Counting in Binary (Base 2)
The prefix “bi-” means two.
The binary system uses only two numbers - 0 and 1.
We count in the binary system the same as in the
decimal system by filling in the place values and
moving up the place value chart.
If the decimal system, base 10 has place values 10x
the previous place - How do you think the place
values for the binary system are determined?

7. Counting in Binary
Do you see a
pattern?
0
1
1 0
1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0

8. Counting in Binary
l
value is 2x the
previous place.
Decima
0
1
2
3
4
5
6
7
8
64’s 32’s 16’s 8’s 4’s 2’s 1’s
0
1
Each place 1 0
previo 1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0

9. Counting in Binary
l
one 4, one 2 = 6
1000 = 8
one 8
Decima
0
1
2
3
4
5
6
7
8
64’s 32’s 16’s 8’s 4’s 2’s 1’s
0
110 = 6 1
one 4, o 1 0
on 1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0

10. Counting in Binary
What is
binary
number?
64’s 32’s 16’s 8’s 4’s 2’s 1’s
1 0 1 0 0 1
this

11. Counting in Binary
41
Determine the
place values
and add
together.
64’s 32’s 16’s 8’s 4’s 2’s 1’s
1 0 1 0 0 1
(32) + (0) + (8) + (0) + (0) + 1=
them

12. Try
counting
to 20.
Counting to 20 in binary
Binary Decimal
1011 11
1100 12
1101 13
1110 14
1111 15
10000 16
10001 17
10010 18
10011 19
10100 20
Binary Decimal
1 1
10 2
11 3
100 4
101 5
110 6
111 7
1000 8
1001 9
1010 10

13. Bits and Bytes
Bit - In the binary system, each
short for binary digit.
0 or 1 is called a bit -
Byte - A group
representation
There are 256
of eight bits. The letter “G” is a
of 1 byte (eight bits).
combinations of bits available 28=256

14. The alphabet in binary
Binary Alphabet
O11OOOO1 a
O11OOO1O b
O11OOO11 c
O11OO1OO d
O11OO1O1 e
O11OO11O f
O11OO111 g
O11O1OOO h
O11O1OO1 i

16. UTF-8
UTF-8 is a character encoding capable
of encoding all possible characters, or
code points, defined by Unicode. The
encoding is variable-length and uses
8-bit code units. It was designed for
backward compatibility with ASCII,
and to avoid the complications of
endianness and byte order marks in
the alternative UTF-16 and UTF-32
encodings.

17. Can you read this?
Binary code is the base code of computer
language.
Once you understand the patterns and the
rules, you can learn other programming
languages.
Have fun coding!
01001000011011110110110001100001001000000110
00110110111101101101011011110010000001100101
01110011011101000110000101110011

18. Engineering notation

19. Sources
Adapted from, Using Information Technology,
Williams/Sawyer

20. Additional Teaching Links
Text to Binary and Back Again
http://www.roubaixinteractive.com/PlayGround/Binary_Conversion/Binary_To_Text.a
sp
The Alphabet in Binary
http://www.tekmom.com/buzzwords/binaryalphabet.html
http://en.wikipedia.org/wiki/Binary_numeral_system