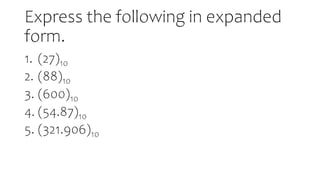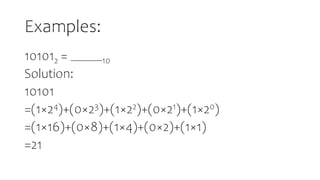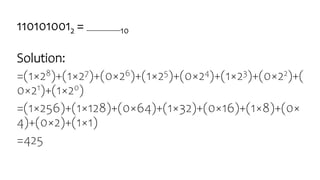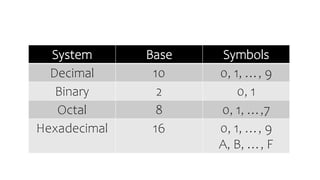
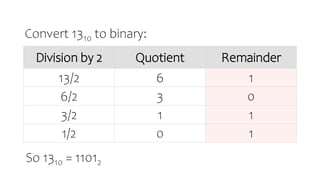
The document discusses different number systems including decimal, binary, octal, and hexadecimal. It provides details on: - What defines a number system and how they are used to represent quantities - The base or radix of a system determines the number of unique symbols used - Decimal uses base-10 with symbols 0-9 and is widely used. Binary uses base-2 with only symbols 0 and 1. - Methods for converting between decimal and binary are presented using division and remainder.

1. NUMBER SYSTEM

2. Number System
The number system or the numeral system is the
system of naming or representing numbers.
A number system is defined as a system of
writing to express numbers. It is the
mathematical notation for representing
numbers of a given set by using digits or other
symbols in a consistent manner.

3. A number system can be used to represent the
number of students in a class or number of
viewers watching a certain TV program etc.
The digital computer represents all kinds of data
and information in binary numbers. It includes
audio, graphics, video, text and numbers.
The total number of digits used in a number
system is called its base or RADIX.

4. The value of any digit in a number can be
determined by:
•The digit
•Its position in the number
•The base of the number system

5. Types of Number System
1. Decimal number system (Base- 10)
2. Binary number system (Base- 2)
3. Octal number system (Base-8)
4. Hexadecimal number system (Base- 16)

6. System Base Symbols
Decimal 10 0, 1, …, 9
Binary 2 0, 1
Octal 8 0, 1, …,7
Hexadecimal 16 0, 1, …, 9
A, B, …, F

7. Decimal Number System
(Base 10 Number System)

8. The number system that we use in our day-to-day life
is the decimal number system.
The way of denoting the decimal numbers with base
10 is also termed as DECIMAL NOTATION.

9. This number system is widely used in computer
applications. It is also called the base-10 number
system which consists of 10 digits, such as,
0,1,2,3,4,5,6,7,8,9.
Each digit in the decimal system has a position
and every digit is ten times more significant than
the previous digit.

10. In the decimal number system, the positions
successive to the left of the decimal point represent
units, tens, hundreds, thousands and so on.
Suppose, 25 is a decimal number, then 2 is ten times
more than 5.
Some examples of decimal numbers are:-
(12)10, (345)10, (119)10,
(200)10, (313.9)10

11. Every position shows a particular power of the
base (10).
For example, the decimal number 1,457 consists of
the digit 7 in the units position, 5 in the tens place,
4 in the hundreds position, and 1 in the thousands
place whose value can be written as
(1×103) + (4×102) + (5×101) + (7×100)
(1×1000) + (4×100) + (5×10) + (7×1)
1000 + 400 + 50 + 7
1,457

12. More examples:
(92)10 = (9×101)+(2×100)
(200)10 = (2×102)+(0x101)+(0x100)
The decimal numbers which have digits present on
the right side of the decimal (.) denote each digit with
decreasing power of 10. Some examples are:
(30.2)10= (3×101)+(0x100)+(2×10-1)
(212.367)10=(2×102)+(1×101)+(2×100)+(3×10-1) +
(6×10-2)+(7×10-3)

13. Express the following in expanded
form.
1. (27)10
2. (88)10
3. (600)10
4. (54.87)10
5. (321.906)10

14. Express the following in Base 10
6. (7×101)+(5×100) =
7. (4×103)+(2×102)+(9×101)+(2×100) =
8. (8×103) + (0×102) + (3×101) + (0×100) =
9. (5×101)+(3x100)+(9×10-1) =
10. (7×102)+(0×101)+(4×100)+(9×10-1)+ (3×10-
2)+(5×10-3) =

16. Binary Number System
(Base 2 Number System)

17. According to digital electronics and
mathematics, a binary number is defined as a
number that is expressed in the binary system or
base 2 numeral system.
It describes numeric values by two separate
symbols; 1 (one) and 0 (zero).
The base-2 system is the positional notation with
2 as a radix.

18. The binary system is applied internally by almost
all latest computers and computer-based
devices because of its direct implementation in
electronic circuits using logic gates.
Every digit is referred to as a BIT.

19. What is Bit in Binary Number?
A single binary digit is called a “Bit”.
A binary number consists of several bits.
Examples are:
10101 is a five-bit binary number
101 is a three-bit binary number
100001 is a six-bit binary number

20. Facts to Remember:
Binary numbers are made up of only 0’s and 1’s.
A binary number is represented with a base-2
A bit is a single binary digit.

21. Converting Decimal Number System
to Binary Number System

22. Convert 1310 to binary:
Division by 2 Quotient Remainder
13/2 6 1
6/2 3 0
3/2 1 1
1/2 0 1
So 1310 = 11012

23. Convert 17410 to binary
=101011102
Convert 5110 to binary
=1100112
Convert 21710 to binary
=110110012
Convert 802310 to binary
=11111010101112

24. Convert the following Decimal
Numbers to Binary Numbers
1. 1610
2. 4310
3. 3910
4. 4710
5. 1310
6. 14510
7. 12410
8. 11610
9. 18210
10.23810

25. Converting Binary Number System to
Decimal Number System

26. Examples:
101012 = 10
Solution:
10101
=(1×24)+(0×23)+(1×22)+(0×21)+(1×20)
=(1×16)+(0×8)+(1×4)+(0×2)+(1×1)
=21

27. 1101010012 = 10
Solution:
=(1×28)+(1×27)+(0×26)+(1×25)+(0×24)+(1×23)+(0×22)+(
0×21)+(1×20)
=(1×256)+(1×128)+(0×64)+(1×32)+(0×16)+(1×8)+(0×
4)+(0×2)+(1×1)
=425

28. Covert the following Binary Numbers to
Decimal Numbers
1. 112
2. 11002
3. 111002
4. 101012
5. 1001012
6. 1111002
7. 10110012
8. 1111112
9. 101000112
10.110110112