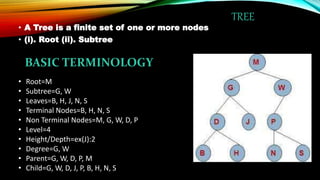
The document provides a comprehensive overview of binary trees, including their structure, terminology, and traversal methods. It explains the representations of binary trees, including array and linked representations, and details three standard traversal techniques: preorder, inorder, and postorder, complete with algorithms for each method. Each traversal method is illustrated with iterative steps to guide the reader through the process of visiting nodes in a binary tree.

1. BINARY TREE REPRESENTATION AND
TRAVERSAL
19IFTE063_K.S.Jothika
19IFTE073_T.G.Preethi

2. TREE
• A Tree is a finite set of one or more nodes
• (i). Root (ii). Subtree
BASIC TERMINOLOGY
• Root=M
• Subtree=G, W
• Leaves=B, H, J, N, S
• Terminal Nodes=B, H, N, S
• Non Terminal Nodes=M, G, W, D, P
• Level=4
• Height/Depth=ex(J):2
• Degree=G, W
• Parent=G, W, D, P, M
• Child=G, W, D, J, P, B, H, N, S

3. BINARY TREE
•A Binary Tree is set of nodes which is either empty or
consists of a root and to disjoint binary trees called LEFT
SUBTREE and RIGHT SUBTREE.
Example of binary tree:
SKEWED BINARY TREE COMPLETE BINARY TREE

4. REPRESENTION OF BINARY TREES
ARRAY REPRESENTATION
(a)The Root R Of T is stored in
TREE[1]
(b)If a node N occupies TREE[K]
then,
• Left child is stored in TREE[2*k]
• Right child is stored in
TREE[2*k+1]
(c)NULL is used to indicate an
empty subtree. TREE[1]=NULL

5. • INFO[K] contains the data at node N
• LEFT[K]=Left child of node N
• RIGHT[K]=Right child of node N
(a)The value ROOT=14 indicates that
harris is the root of the tree.
(b)LEFT[14]=9 indicates that cohen is
the left child of harris,
RIGHT[14]=7 indicates that lewis is the
right child of harris
(c)Repeating step (b) untill reach the
NULL
LINKED REPRESENTATION

6. TRAVERSING BINARY TREES
Tree Traversal is the process of visiting each node in
the tree exactly once
There are three standard ways of traversing a binary
tree T with Root R.
• Preorder
• Inorder
• postorder

7. PREORDER TRAVERSAL
ITeRATION
1. STACK:NULL set PTR=A
2. STACK:NULL, C Process B
3. STACK:NULL, C Process D
4. STACK: NULL, C, H Process G
5. STACK:NULL, C PTR=H
6. STACK:NULL, C, K No Left child
7. STACK:NULL, C Process K
8. STACK:NULL Process C
9. STACK:NULL, F Process E
10. STACK:NULL, popout F and Process F
A, B, D, G, H, K, C, E, F

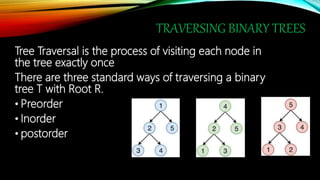
8. PREORDER TRAVERSAL ALGORITHM
PREORD(INFO, LEFT, RIGHT, ROOT)
• [Initially push NULL onto STACK, andIinitialize PTR. ]
Set TOP:=1, STACK[1]:=NULL and PTR:=ROOT.
• Repeat Steps 3 to 5 while PTR!= NULL:
• Apply PROCESS to INFO[PTR].
• [Right child?]
If RIGHT[PTR]!=NULL, then:[Push on STACK. ]
Set TOP:=TOP+1, and STACK[TOP]:=RIGHT[PTR].
[End of If structure]
• [Left child? ]
If LEFT[PTR]!=NULL, then:
Set PTR:=LEFT[PTR].
Else:[Pop from STACK. ]
Set PTR:=STACK[TOP] and TOP:=TOP-1.
[End of if structure. ]
[End of step 2 loop. ]
• Exit.

9. INORDER TRAVERSAL
ITeRATION
1. STACK:NULL set PTR=A
2. STACK:NULL,A, B, D, G, K
3. STACK:NULL,A, B Set PTR:=H
4. PTR:H, STACK:NULL, A, B, H, L
5. STACK:NULL,A, B Set PTR:=M
6. STACK:NULL,A,B,M
7. STACK:NULL,PTR=C
8. PTR=C, STACK:NULL ,C, E
9. [BT]E, C
K, G, D, L, H, M, B, A, E, C

10. INORDER TRAVERSAL ALGORITHM
INORD(INFO, LEFT, RIGHT, ROOT)
• [Push NULL onto STACK and initialize PTR. ]
Set TOP:=1, STACK[1]:=NULL and
PTR:=ROOT.
• Repeat while PTR!=NULL:[Pushes left most
path onto stack. ]
(a) Set TOP:=TOP+1 and STACK[TOP]:=PTR.
[Saves node. ]
(b) Set PTR:=LEFT[PTR]. [Updates PTR. ]
[End of loop. ]
• Set PTR:=STACK[TOP] and TOP:=TOP-1.
[ Pops node from STACK. ]
• Repeat Steps 5 to 7 while
PTR!=NULL:[Backtracking. ]
• Apply PROCESS to INFO[PTR].
• [Right child?] If RIGHT[PTR]!=NULL, then:
(a) Set PTR:=RIGHT[PTR].
(b) Go to step 2.
[ End of if structure. ]
• Set PTR:=STACK[TOP] and TOP:=TOP-1.[Pops node]
[End of step 4 loop. ]
• Exit.

11. POSTORDER TRAVERSAL
ITeRATION
1. STACK:=NULL set PTR:=A
2. STACK:=NULL,A,-C, B,D,-H, G, K
3. POP K, G, -H STACK:NULL,A, -C, B, D PTR=-H
Reset PTR:=H
4. PTR:H, STACK:NULL, A,-C, B, D, H, -M, L
5. Pop L, -M
6. PTR=M STACK:NULL,A,-C, B, D, H, M Pop M, H,
D, B, -C PTR=C
7. PTR=C, STACK:NULL ,A, C, E
Pop and Process E, C, AK, G, L, M, H, D, B, E, C, A

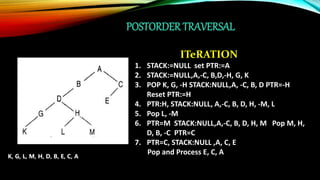
12. POSTORDER TRAVERSAL ALGORITHM
• Set PTR:=SRACK[TOP] and TOP:=TOP-
1.
[Pops node from STACK. ]
• Repeat while PTR>0;
(a) Apply PROCESS to INFO[PTR].
(b) Set PTR:=STACK[TOP] and
TOP:=TOP-1.
[ Pops node from STACK. ]
[End of loop. ]
• If PTR<0, then :
(a) Set PTR:=-PTR.
(b) Go to step 2.
[ End of if structure. )
• Exit.
POSTORD(INFO, LEFT, RIGHT, ROOT)
• [Push NULL onto STACK and initialize PTR.
]
Set TOP:=1, STACK[1]:=NULL and
PTR:=ROOT.
• [Push left most path onto stack. ]
Repeat Steps 3 to 5 while PTR!= NULL:
• Set TOP:=TOP+1 and STACK[TOP]:=PTR.
[Pushes PTR on STACK. ]
• If RIGHT[PTR]!=NULL, then:[Push on
STACK. ]
Set TOP:=TOP+1 and
STACK[TOP]:=RIGHT[PTR].
[End of If structure]
• Set PTR:=LEFT[PTR]. [Updates pointer