This document discusses dependent type semantics (DTS) as a framework for natural language semantics that employs dependent type theory. It highlights the proof-theoretic aspects of DTS and presents updates to the type checking and inference system that facilitate presupposition projection calculations. Key concepts such as Curry-Howard correspondence, dependent types, and their applications in linguistic semantics are examined, along with references to previous works in the field.

















![DTT DTS Previous work Type check./infer. Conclusion References
Dependent function type
Introduction rules Elimination rules
function type
→ in STLC
x : A....
M : B
i
λx.M
function
: A → B
(LAM ),i
M : A → B N : A
MN : B
(APP)
Dependent
function type
(Π) in DTT
A : sort
x : A....
M : B
i
λx.M
function
: (x:A) → B
(ΠI ),i
M : (x:A) → B N : A
MN : B[N/x]
(ΠE)
Scope: (x:A) → B
14 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-18-320.jpg)
![DTT DTS Previous work Type check./infer. Conclusion References
Dependent sum type
Introduction rules Elimination rules
product
type ×
in STLC
M : A N : B
(M, N)
pair
: A × B
(PROD)
M : A × B
π1(M) : A
(PROJ)
M : A × B
π2(M) : B
(PROJ)
Dependent
sum type
(Σ) in
DTT
M : A N : B[M/x]
(M, N)
pair
:
x:A
B
(ΣI )
M :
x:A
B
π1(M) : A
(ΣE)
M :
x:A
B
π2(M) : B[π1(M)/x]
(ΣE)
Scope:
x:A
B
15 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-19-320.jpg)

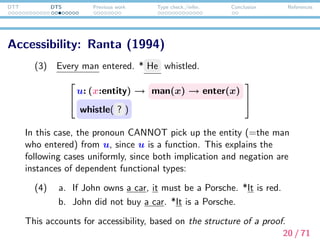
![DTT DTS Previous work Type check./infer. Conclusion References
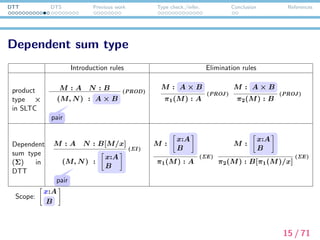
E-type anaphora: Ranta (1994)
(1) A man entered. He whistled.
u:
x:entity
man(x)
enter(x)
whistle( π1(u) )
Note:
x:A
B
is a type for pairs of A and B[x].
18 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-22-320.jpg)
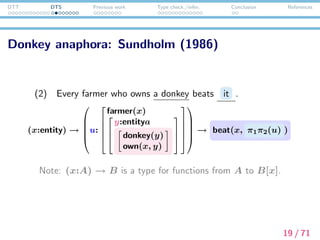
![DTT DTS Previous work Type check./infer. Conclusion References
Donkey anaphora: Sundholm (1986)
(2) Every farmer who owns a donkey beats it .
(x:entity) →
u:
farmer(x)
y:entitya
donkey(y)
own(x, y)
→ beat(x, π1π2(u) )
Note: (x:A) → B is a type for functions from A to B[x].
19 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-23-320.jpg)












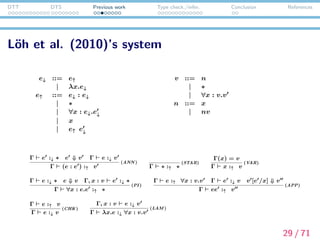
![DTT DTS Previous work Type check./infer. Conclusion References
L¨oh et al. (2010)’s system
e↓ ::= e↑
| λx.e↓
e↑ ::= e↓ : e↓
| ∗
| ∀x : e↓.e↓
| x
| e↑ e↓
v ::= n
| ∗
| ∀x : v.v
n ::= x
| nv
Γ e :↓ ∗ e ⇓ v Γ e :↓ v
Γ (e : e ) :↑ v
(ANN )
Γ ∗ :↑ ∗
(STAR)
Γ(x) = v
Γ x :↑ v
(VAR)
Γ e :↓ ∗ e ⇓ v Γ, x : v e :↓ ∗
Γ ∀x : e.e :↑ ∗
(PI )
Γ e :↑ ∀x : v.v Γ e :↓ v v [e /x] ⇓ v
Γ ee :↑ v
(APP)
Γ e :↑ v
Γ e :↓ v
(CHK)
Γ, x : v e :↓ v
Γ λx.e :↓ ∀x : v.v
(LAM )
29 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-38-320.jpg)
![DTT DTS Previous work Type check./infer. Conclusion References
Explanation about L¨oh’s system
Typing rules are also classified into two categories:
type inference rules and type checking rules.
Γ e :↓ ∗ e ⇓ v Γ e :↓ v
Γ (e : e ) :↑ v
(ANN )
Γ ∗ :↑ ∗
(STAR)
Γ(x) = v
Γ x :↑ v
(VAR)
Γ e :↓ ∗ e ⇓ v Γ, x : v e :↓ ∗
Γ ∀x : e.e :↑ ∗
(PI )
Γ e :↑ ∀x : v.v Γ e :↓ v v [e /x] ⇓ v
Γ ee :↑ v
(APP)
The conclusion of type inference rules contains :↑
31 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-40-320.jpg)

![DTT DTS Previous work Type check./infer. Conclusion References
How to read typing rules
Example
[L] Γ σ M :↑ (x:v) → v [L ] [L ] Γ σ N :↓ v [L ] v [N/x] β v
[L] Γ σ MN :↑ v [L ]
(ΠE)
In logic:
We read rules from premise to conclusion.
If the premises are satisfied, then the conclusion is satisfied.
33 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-42-320.jpg)
![DTT DTS Previous work Type check./infer. Conclusion References
How to read typing rules
Example
[L] Γ σ M :↑ (x:v) → v [L ] [L ] Γ σ N :↓ v [L ] v [N/x] β v
[L] Γ σ MN :↑ v [L ]
(ΠE)
In type inference:
We read rules from conclusion to premise.
A term to the left of the colon has a type to the right of the
colon only when all the premise are satisfied.
34 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-43-320.jpg)




![DTT DTS Previous work Type check./infer. Conclusion References
Typing rules
Constant symbols
(c, v) ∈ σ
[L] Γ σ c :↑ v [L]
(CON )
@-operators
[L] Γ σ @i :↓ v [L, (i : v)]
(ASP)
σ : signature
[L] : type assignments for @-operators
38 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-48-320.jpg)
![DTT DTS Previous work Type check./infer. Conclusion References
Typing rules
Dependent sum types
[L] Γ σ A :↓ s1 [L ] A β v [L ] Γ, x : v σ B :↓ s2 [L ]
[L] Γ σ
x:A
B
:↑ s2 [L ]
(ΣF)
(s1, s2 ∈ {type, kind})
[L] Γ σ M :↓ v [L ] v [M/x] β v [L ] Γ σ N :↓ v [L ]
[L] Γ σ (M, N) :↓
x:v
v
[L ]
(ΣI )
[L] Γ σ M :↑
x:v
v
[L ]
[L] Γ σ π1M :↑ v [L ]
(ΣE)
[L] Γ σ M :↑
x:v
v
[L ] v [π1M/x] β v
[L] Γ σ π2M :↑ v [L ]
(ΣE)
39 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-49-320.jpg)




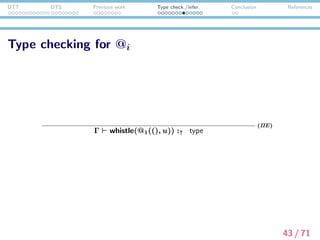

![DTT DTS Previous work Type check./infer. Conclusion References
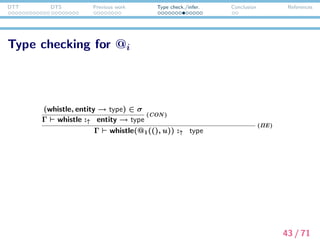
Type checking for @i
Why this fails?
(ΠE) rule
Γ σ M :↑ (x:v) → v Γ σ N :↓ v v [N/x] β v
Γ σ MN :↑ v
(ΠE)
Because (ΠE) rule first tries to infer the type of the function
part of a function application term.
This conflicts with the fact that @i is not an inferable term.
44 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-57-320.jpg)
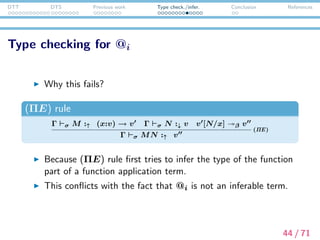

![DTT DTS Previous work Type check./infer. Conclusion References
Type checking for @i
(→E) rule
[L] Γ σ N :↑ v [L ] [L ] Γ σ M :↓ v → v [L ]
[L] Γ σ MN :↓ v [L ]
(→E)
In this rule, the argument part of function application is
evaluated first.
We can do type inference of the sentence (1) by using this
rule.
47 / 71](https://image.slidesharecdn.com/bekkisatotytles2015-150805074841-lva1-app6891/85/Calculating-Projections-via-Type-Checking-60-320.jpg)