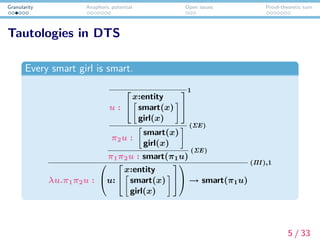
The document discusses the proof-theoretic approach to semantics, focusing on granularity, anaphoric potential, and open issues related to dependent type semantics. It contrasts model-theoretic and proof-theoretic semantics, highlighting how the latter can better capture nuances in natural language meaning through verification conditions. Additionally, it addresses the limitations of dynamic semantics and the empirical and computational motivations for adopting proof-theoretic methods in understanding anaphoric relationships.

1. Granularity Anaphoric potential Open issues Proof-theoretic turn
Introduction to Dependent Type Semantics:
A proof-theoretic turn in natural language
semantics
Daisuke Bekki1,2 Koji Mineshima1,2
1Ochanomizu University / 2CREST, Japan Science and Technology Agency
version: August 19, 2016
ESSLLI 2016 course, Bolzano, Italy, August 15-19, 2016.
1 / 33

2. Granularity Anaphoric potential Open issues Proof-theoretic turn
Remarks on Granularity
2 / 33

3. Granularity Anaphoric potential Open issues Proof-theoretic turn
Granularity of meaning
Model-theoretic semantics does not distinguish tautologies
(Francez, 2014):
(1) a. Every girl is a girl.
b. Every boy is a boy.
(2) a. Every smart girl is smart.
b. Every smart boy is smart.
Intuition:
(1a) and (1b) are similar (but still different).
(2a) and (2b) are similar (but still different).
(1a) and (2a) are similar (but still different).
(1b) and (2b) are similar (but still different).
3 / 33

4. Granularity Anaphoric potential Open issues Proof-theoretic turn
Tautologies in DTS
Every girl is a girl.
u :
x:entity
girl(x)
1
π2u : girl(π1u)
(ΣE)
λu.π2u : u:
x:entity
girl(x)
→ girl(π1u)
(ΠI ),1
4 / 33

5. Granularity Anaphoric potential Open issues Proof-theoretic turn
Tautologies in DTS
Every smart girl is smart.
u :


x:entity
smart(x)
girl(x)


1
π2u :
smart(x)
girl(x)
(ΣE)
π1π2u : smart(π1u)
(ΣE)
λu.π1π2u :

u:


x:entity
smart(x)
girl(x)



 → smart(π1u)
(ΠI ),1
5 / 33

6. Granularity Anaphoric potential Open issues Proof-theoretic turn
Tautologies in DTS
(1) a. Every girl is a girl.
λu.π2u: u:
x:entity
girl(x)
→ girl(π1u)
b. Every boy is a boy.
λu.π2u: u:
x:entity
boy(x)
→ boy(π1u)
Similarity btw. (1a) and (1b): the same proof term
Difference btw. (1a) and (1b): different types
6 / 33

7. Granularity Anaphoric potential Open issues Proof-theoretic turn
Tautologies in DTS
(2) a. Every smart girl is smart.
λu.π1π2u:

u:


x:entity
smart(x)
girl(x)



 → smart(π1u)
b. Every smart boy is smart.
λu.π1π2u:

u:


x:entity
smart(x)
boy(x)



 → smart(π1u)
Similarity btw. (2a) and (2b): the same proof term
Difference btw. (2a) and (2b): different types
7 / 33

8. Granularity Anaphoric potential Open issues Proof-theoretic turn
Granularity in proof-theoretic semantics
For a theory of meaning, granularity is a measure of the
information they provide for distinguishing difference in their
meanings.
Proof-theoretic semantis in terms of dependent types provides
an appropreate level of abstraction on similarity/difference
between tautologies.
8 / 33

9. Granularity Anaphoric potential Open issues Proof-theoretic turn
Anaphoric potential
9 / 33

10. Granularity Anaphoric potential Open issues Proof-theoretic turn
Anaphoric potential
The sentences (3a) and (4a) are truth-conditionally equivalent (cf.
∃x(Lx ∧ Rx) ≡ ¬∀x(Lx → ¬Rx)), while they show the
different anaphoric potential to the subsequent sentences.
(3) a. Some linguist is rich.
b. He/She does not even have to teach.
(4) a. It is not the case that no linguist is rich.
b. * He/She does not even have to teach.
Therefore, truth-conditinal semantics is not enough for
distinguishing a certain aspect of the meaning of sentences.
(Kamp et al. (2011))
10 / 33

11. Granularity Anaphoric potential Open issues Proof-theoretic turn
Anaphoric potential in DRT
Some linguist is rich.
He/she does not even
have to teach.
x
linguist(x)
rich(x)
¬
z
haveToTeach(z)
z =?
It is not the case that no linguist is rich.
*He/she does not even have to teach.
¬
x
linguist(x)
⇐ ¬ rich(x)
¬
z
haveToTeach(z)
z =?
x is accessible from z. x is not accessible from z.
11 / 33

12. Granularity Anaphoric potential Open issues Proof-theoretic turn
Anaphoric potential in DTS
Some linguist is rich.
He/she does not even
have to teach.
It is not the case that no linguist is rich.
He/she does not even have to teach.




u:


x:entity
L(x)
R(x)


¬HTT(@1entity)




u:¬ (x:entity) → L(x) → ¬R(x)
¬HTT(@1entity)
@1entity = π1u @1entity =??
12 / 33

13. Granularity Anaphoric potential Open issues Proof-theoretic turn
Anaphoric potential in DTS
However, if the following inference had a proof term f u, then
the anaphoric link in question would be wrongly predicted to be
licenced.
u : ¬ (x:entity) → L(x) → ¬R(x)


x:entity
L(x)
R(x)

 true
Proof search:
entity : type
(CON )
u : ¬ (x:entity) → L(x) → ¬R(x)
f u :


x:entity
L(x)
R(x)


?
π1( f u) : entity
(ΣE)
@1entity : entity
(@)
13 / 33

14. Granularity Anaphoric potential Open issues Proof-theoretic turn
Proof of u : ¬((x:e) → Lx → ¬Rx)


x:e
Lx
Rx

 true
u: ¬((x:e) → Lx → ¬Rx)
x: e
3
l: Lx
2
r: Rx
1
(l, r):
Lx
Rx
(ΣI )
(x, (l, r)):


x:e
Lx
Rx


(ΣI )
y: ¬


x:e
Lx
Rx


4
y(x, (l, r)): ⊥
(→E)
λr.y(x, (l, r)): ¬Rx
(¬I ),1
λl.λr.y(x, (l, r)): Lx → ¬Rx
(→I ),2
λx.λl.λr.y(x, (l, r)): (x:e) → Lx → ¬Rx
(ΠI ),3
u(λx.λl.λr.y(x, (l, r))): ⊥
(→E)
λy.u(λx.λl.λr.y(x, (l, r))): ¬¬


x:e
Lx
Rx


(¬I ),4
dne(λy.u(λx.λl.λr.y(x, (l, r)))):


x:e
Lx
Rx


(DNE)
14 / 33

15. Granularity Anaphoric potential Open issues Proof-theoretic turn
Proof of u : ¬((x:entity) → Lx → ¬Rx)


x:entity
Lx
Rx

 true
This does not hold in intuitionistic settings, such as DTT and
UDTT.
It requires classical settings, such as
DTT/UDTT+(DNE)-rule
M: ¬¬A
dne(M): A
(DNE)
15 / 33

16. Granularity Anaphoric potential Open issues Proof-theoretic turn
Proof-theoretic hierarchy
NK = NM + DNE (i.e.¬¬A → A)
NK = NJ + LEM (i.e.¬A ∨ A)
NJ = NM + EFQ (i.e.⊥ → A)
(3a) Some linguist is rich.
(4a) It is not the case that no linguist is rich.
The difference in anaphoric potentials of (3a) and (4a) is due
to the fact that
(3a) NM (4a)
(4a) NK (3a)
are theorems of different proof systems.
Proof-theoretic semantics provides a distinction between
truth-conditionally equivalent propositions. 16 / 33

17. Granularity Anaphoric potential Open issues Proof-theoretic turn
Open issues on anaphoric potential
17 / 33

18. Granularity Anaphoric potential Open issues Proof-theoretic turn
A toilet in a funny place
Similar argument applies to the following case discussed in
Karttunen (1976), Krahmer and Muskens (1995), Geurts (1999):
(5) a. Either there is no toilet , or it is in a funny place.
If disjunction in DTT is defined (instead of ) as
A ∨ B
def
≡ ¬A → B, then we can deduce “there is a toilet” from
a doubly-negated form “¬¬ there is a toilet” (Bekki, 2013)
18 / 33

19. Granularity Anaphoric potential Open issues Proof-theoretic turn
A toilet in a funny place
However, this analysis is not on a right track, since it predicts that
the following anaphoric link is licenced if the use of dne is allowed
in DTS, which is not the case.
(6) It is not the case that nobody showed up.
* He/she was sitting alone.
Thus we need the other analysis for this case. But the following
cases implies that we have to be careful about the status of the
original paradigm:
(7) Either John is not married , or * she is not home right
now.
(8) It is not the case that there is no toilet in this building.
Actually, it is in a funny place.
19 / 33

20. Granularity Anaphoric potential Open issues Proof-theoretic turn
Hidden marbles
A well-known example showing that “discourse referents are not
introduced solely by inferences”. (by Barbara Partee, due to Heim
(1982))
(9) Nine balls out of ten are found in the bag. * It must be
under the sofa.
We should reconsider this case from a proof-theoretic perspective
whether (9) can be proven in a intuitionistic setting.
There are exactly ten balls.
Exactly nine balls are found.
?? There is a ball that is not found.
In this way, DTS provides a new perspective that differentiates the
status of various constructions from the viewpoint of proof-theory.
20 / 33

21. Granularity Anaphoric potential Open issues Proof-theoretic turn
Proof-theoretic turn in natural
language semantics
21 / 33

22. Granularity Anaphoric potential Open issues Proof-theoretic turn
Dynamic turn in natural language semantics
Frege
−→ Tarski model-theoretic sem. of math.
−→ Gentzen, Pravitz, Martin-L¨of proof-theoretic sem. of math.
−→ Davidson, Montague model-theoretic sem. of single sentences
−→ Dummett proof-theoretic sem. of single sentences
Dynamic turn
−→ Kamp, Heim, Asher, model-theoretic sem. of discourse
Groenendijk and Stokhof
−→ Sundholm, Ranta, Cooper proof-theoretic sem. of discourse
Anaphoric potential (partly) motivated a dynamic turn on the
meaning of a sentence/discourse: form truth-condition to
context-change potential (or information update)
We challenge it empirically and conceptually.
22 / 33

23. Granularity Anaphoric potential Open issues Proof-theoretic turn
Reconsider context-change potential
Empirically: dynamic semantics can hardly handle the following
data:
Syllogistic anaphora (2nd day)
Bridging (3rd day)
Factive presupposition (3rd day)
Disjunctive antecedent (4th day)
⇐
We have seen how these cases could be handled in DTS.
23 / 33

24. Granularity Anaphoric potential Open issues Proof-theoretic turn
Reconsider context-change potential
Conceptually: “CCP” does not signify the core of dynamic
semantics. Even FoL-semantics, a proposition changes a given
context:
1. Either John or Bill is in the kitchen.
2. Bill is not in the kitchen.
2. updates the context from K(j ) ∨ B(j ) to K(j ) ∨ B(j ), ¬B(j )
(then we can deduce K(j )).
Therefore, the point at issue is not whether the meaning of a
sentence changes/updates a given context. The points are:
How contexts are represented in the theory
How the meaning of a sentence changes/updates them
24 / 33

25. Granularity Anaphoric potential Open issues Proof-theoretic turn
Reconsider context-change potential
In DRT/DPL:
A context is an assignment (or a set of possible worlds, or
other complex).
A proposition changes/updates a context as a side effect .
DRT/DPL semantics has its origin in dynamic logic (Fischer
and Ladner, 1977)(Harel, 1979), an axiomatic semantics of
programming languages that embeds side-effects in modal
logic)
cf. Monadic semantics, continuation semantics
In DTS:
A context is a list of proof-proposition (=term-type) pairs.
A proposition changes/updates it by just adding itself to it
(no side effetcs).
25 / 33

26. Granularity Anaphoric potential Open issues Proof-theoretic turn
Beyond context-change potential
1st day The foundation of dependent type semantics:
Proof-theoretic semantics, natural deduction,
Curry-Howard correspondence and dependent types
2nd-4th days Empirical aspects of natural language meaning, in
particular, those traditionally pursued in dynamic
semantics, are more precisely modelled by using DTS
(=dependent type theory + underspecified terms)
5th day Computational aspects of natural language meaning
is necessary, both for testability of the theory and for
applications of the theory to such tasks as RTE.
We regard this as a proof-theoretic turn of natural
language semantics.
26 / 33

27. Granularity Anaphoric potential Open issues Proof-theoretic turn
Beyond context-change potential
Since this proof-theoretic turn of natural language semantics
is both empirically and computationally driven, it forces a shift
from model-theoretic semantics to proof-theoretic semantics
In proof-theoretic semantics:
The core meaning of a logical operator lies in its
verification condition(s)
The core meaning of a proposition is
the intension of its proofs (or its proof-condition) i.e. by
what it is verified in proof diagrams
Underspecified terms @ gives another spin on the whole
setting
27 / 33

28. Granularity Anaphoric potential Open issues Proof-theoretic turn
Thank you!
28 / 33

29. References
Appendix
29 / 33

30. References
Beyond context-change potential
Dependent types theory is a double-decker:
type: kind ⇐ the roof
(x:A) → B: type ⇐ the 2nd floor
λx.M: (x:A) → B ⇐ the 1st floor
The rules always has dual faces:
Introductoin rule for (x:A) → B is Formation rule for λx.M
Elimination rule for (x:A) → B is Formation rule for MN
Formation rule for (x:A) → B is Introduction rule for type
30 / 33

31. References
Reference I
Bekki, D. (2013) “A Type-theoretic Approach to Double Negation
Elimination in Anaphora”, In the Proceedings of Logic and
Engineering of Natural Language Semantics 10 (LENLS 10).
Tokyo.
Fischer, M. and R. Ladner. (1977) “Propositional Modal Logics of
programs”, In the Proceedings of 9th ACM Annual Symposium
on Theory of Computing. pp.286–294.
Francez, N. (2014) “The Granularity of Meaning in
Proof-Theoretic Semantics”, In: N. Asher and S. V. Soloviev
(eds.): Logical Aspects of Computational Linguistics (8th
international conference, LACL2014, Toulouse, France, June
2014 Proceedings), LNCS 8535. Toulouse, Springer, pp.96–106.
Geurts, B. (1999) Presuppositions and pronouns. Elsevier, Oxford.
31 / 33

32. References
Reference II
Harel, D. (1979) First-Order Dynamic Logic, Lecture Notes in
Computer Science. Springer.
Heim, I. (1982) “The Semantics of Definite and Indefinite Noun
Phrases”, Ph.d dissertation, University of Massachusetts.
Published 1989 by Garland Press, New York.
Kamp, H., J. van Genabith, and U. Reyle. (2011) “Discourse
Representation Theory”, In: G. D.M. and F. G unthner (eds.):
Handbook of Philosophical Logic, Vol. 15. Doredrecht, Springer,
pp.125–394.
Karttunen, L. (1976) “Discourse Referents”, In: J. D. McCawley
(ed.): Syntax and Semantics 7: Notes from the Linguistic
Underground, Vol. 7. New York, Academic Press, pp.363–85.
32 / 33

33. References
Reference III
Krahmer, E. and R. Muskens. (1995) “Negation and Disjunction in
Discourse Representation Theory”, Journal of Semantics 12(4),
pp.357–376.
33 / 33