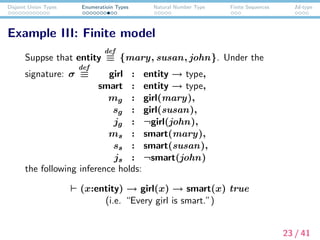
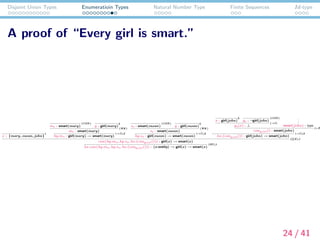
The document discusses disjoint union types, enumeration types, natural number types, finite sequences, and id-types within the context of dependent type semantics. It presents definitions and rules for disjoint union types, illustrating how they can represent disjunctions and how to apply elimination rules for these types. The document also includes examples and applications, highlighting their relevance in dynamic semantics and proof search.

1. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Introduction to Dependent Type Semantics:
More dependent types
Daisuke Bekki1,2 Koji Mineshima1,2
1Ochanomizu University / 2CREST, Japan Science and Technology Agency
version: August 18, 2016
ESSLLI 2016 course, Bolzano, Italy, August 15-19, 2016.
1 / 41

2. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Disjoint Union Types for Disjunction
2 / 41

3. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Disjoint union type A B is a type for representing disjunctions
(A ∨ B).
Definition ( -Formation/Introduction Rules)
A : type B : type
A B : type
( F)
M : A
ι1(M) : A B
( I )
N : B
ι2(N) : A B
( I )
3 / 41

4. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Mary sees a horse or a pony: Parsing
Mary
NP
m
sees
SNP/NP
see
a
SNP(SNP/NP)/N
λn.λp.λx.

 v:
y:entity
ny
p(π1(v))x


horse
N
horse
SNP(SNP/NP)
λp.λx.

 v:
y:entity
horse(y)
p(π1(v))x


>
or
CONJ
a
SNP(SNP/NP)/N
λn.λp.λx.

 v:
y:entity
ny
p(π1(v))x


pony
N
pony
SNP(SNP/NP)
λp.λx.

 v:
y:entity
pony(y)
p(π1(v))x


>
SNP(SNP/NP)
λp.λx.

 v:
y:entity
horse(y)
p(π1(v))x



 v:
y:entity
pony(y)
p(π1(v))x


Φ
SNP
λx.

 v:
y:entity
horse(y)
see(x, π1(v))



 v:
y:entity
pony(y)
see(x, π1(v))


<
S
 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


<
4 / 41

5. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Disjoint Union Type: the elimination rule
-Elimination rule is about how to use L of type A B:
Definition ( -Elimination Rule)
L : A B C : (A B) → type
x : A....
M : C(ι1(x))
i
x : B....
N : C(ι2(x))
i
case L of (λx.M; λx.N) : C(L)
( E),i
C is a one-place predicate.
M is a proof that C(x) holds for any x of type A.
N is a proof that C(x) holds for any x of type B.
These are enough for proving that C(L) holds for any L of
type A B.
5 / 41

6. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Example: a disjunctive inference
Mary sees a horse or a pony. =
⇐
Mary sees an animal.
u :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)



 v:
y:entity
animal(y)
see(m, π1v)

 true
under a signature:
k1 : u:
x:entity
horse(x)
→ animal(π1u) “Every horse is an animal.”
k2 : u:
x:entity
pony(x)
→ animal(π1u) “Every pony is an animal.”
6 / 41

7. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Mary sees a horse or a pony.
⇐
Mary sees an animal.
u :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


π1x :
y:entity
horse(y)
(ΣE)
π1π1x : entity
(ΣE)
x :

 v:
y:entity
horse(y)
see(m, π1v)


1
π1x :
y:entity
horse(y)
(ΣE)
k1 : u:
x:entity
horse(x)
→ animal(π1u)
k1(π1x) : animal(π1π1x)
(ΣE)
(π1π1x, k1(π1x)) :
y:entity
animal(y)
(ΣI )
x :

 v:
y:entity
horse(y)
see(m, π1v)


1
π2x : see(m, π1π1x)
(ΣE)
((π1π1x, k1(π1x)), π2x) :

 v:
y:entity
animal(y)
see(m, π1v)


(ΣI )
x :

 v:
y:entity
pony(y)
see(m, π1v)


....
((π1π1x, k2(π1x)), π2x)
:

 v:
y:entity
animal(y)
see(m, π1v)


1
case u of (λx.((π1π1x, k1(π1x)), π2x); λx.((π1π1x, k2(π1x)), π2x)) :

 v:
y:entity
animal(y)
see(m, π1v)


( E),1
7 / 41

8. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
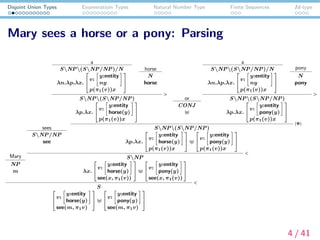
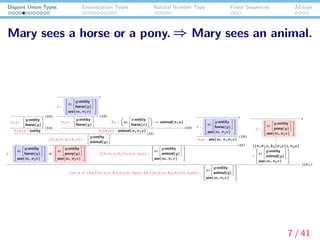
Disjunctive antecedents
Elbourne (2011):
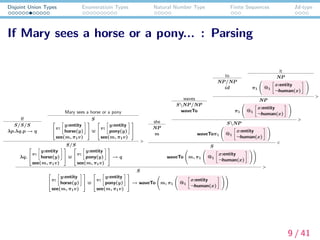
(1) If Mary1 sees [[a horse] or [a pony]]2, she1 waves to it2.
Dynamic semantics does not have a straightforward solution
for it.
A solution via dependent types: Ranta (1994)
8 / 41

9. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
If Mary sees a horse or a pony... : Parsing
If
S/S/S
λp.λq.p → q
Mary sees a horse or a pony
S
 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


S/S
λq.

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)

 → q
>
she
NP
m
waves
SNP/NP
waveTo
to
NP/NP
id
it
NP
π1 @1
x:entity
¬human(x)
NP
π1 @1
x:entity
¬human(x)
>
SNP
waveToπ1 @1
x:entity
¬human(x)
>
S
waveTo m, π1 @1
x:entity
¬human(x)
<
S
 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)

 → waveTo m, π1 @1
x:entity
¬human(x)
>
9 / 41

10. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
If Mary sees a horse or a pony... : Type Checking
....
 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)

 : type
waveTo : entity → entity → type
(CON )
....
x:entity
¬human(x)
: type
p :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


....
x:entity
¬human(x)
1
@1
x:entity
¬human(x)
:
x:entity
¬human(x)
(@)
π1 @1
x:entity
¬human(x)
: entity
(ΣE)
waveTo π1 @1
x:entity
¬human(x)
: entity → type
(→E)
m : entity
(CON )
waveTo m, π1 @1
x:entity
¬human(x)
: type
(→E)

p:

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)



 → waveTo m, π1 @1
x:entity
¬human(x)
: type
(ΠF)
10 / 41

11. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
If Mary sees a horse or a pony... : Proof Search
....
 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)

 : type
waveTo : entity → entity → type
(CON )
....
x:entity
¬human(x)
: type
p :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


....
case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
:
x:entity
animal(x)
1
π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: entity
(ΣE)
p :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


....
case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
:
x:entity
animal(x)
1
k3 : u:
x:entity
animal(x)
→ ¬human(π1u)
(CON )
k3 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: ¬human(π1)
(→E)
π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
, k3 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
:
x:entity
¬human(x)
(→E)
@1
x:entity
¬human(x)
:
x:entity
¬human(x)
(@)
π1 @1
x:entity
¬human(x)
: entity
(ΣE)
waveTo π1 @1
x:entity
¬human(x)
: entity → type
(→E)
m : entity
(CON )
waveTo m, π1 @1
x:entity
¬human(x)
: type
(→E)

p:

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)



 → waveTo m, π1 @1
x:entity
¬human(x)
: type
(ΠI ),1
11 / 41

12. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
If Mary sees a horse or a pony... : @-Elimination
....
 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)

 : type
waveTo : entity → entity → type
(CON )
....
x:entity
¬human(x)
: type
p :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


....
case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
:
x:entity
animal(x)
1
π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: entity
(ΣE)
p :

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)


....
case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
:
x:entity
animal(x)
1
k3 : u:
x:entity
animal(x)
→ ¬human(π1u)
(CON )
k3 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: ¬human(π1)
(→E)
π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
, k3 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
:
x:entity
¬human(x)
(→E)
π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: entity
(ΣE)
waveTo π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: entity → type
(→E)
m : entity
(CON )
waveTo m, π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: type
(→E)

p:

 v:
y:entity
horse(y)
see(m, π1v)



 v:
y:entity
pony(y)
see(m, π1v)



 → waveTo m, π1 case p of
λx.((π1π1x, k1(π1x)), π2x);
λx.((π1π1x, k2(π1x)), π2x)
: type
(ΠI ),1
12 / 41

13. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Inaccessibility again
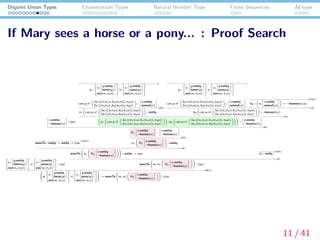
(1) If Mary1 sees [[a horse] or [a pony]], she1 waves to it2.
(2) * If Mary1 sees [[a horse] or [nothing]], she1 waves to it2.
(3) * If Mary1 sees [[nothing] or [a horse]], she1 waves to it2.
(4) If Mary1 sees [[a horse] or [nothing]], she1 is unhappy.
13 / 41

14. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Summary: Disjoint union type and disjunction
Disjunctive constructions are represented by using disjoint
union types.
Disjunctive antecedents have been problematic to dynamic
semantics, while disjoint union types give it a proper analysis,
which implies that anaphora binding is not an issue of variable
binding but an issue of proof construction.
14 / 41

15. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Enumeration Type
15 / 41

16. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Rules for enumeration type
An enumeration type is a type that is inhabited by a finite number
of terms. A particular enumeration type is defined from a given
enumeration of n-number of constructors a1, . . . , an.
Definition ({}-Formation/Introduction Rules)
For each i such that 1 ≤ i ≤ n:
{a1, . . . , an} : type
({}F)
ai : {a1, . . . , an}
({}I )
16 / 41

17. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Rules for enumeration type
Definition ({}-Elimination Rule)
M : {a1, . . . , an} C : {a1, . . . , an} → type N1 : C(a1) . . . Nn : C(an)
caseM (N1, . . . , Nn) : C(M)
({}E)
{}-Elimination rule says how to use M, a proof of an
enumeration type. Similar to disjoint union type.
C is a one-place predicate.
Ni is a proof of C(M) in case M is ai.
caseM (N1, . . . , Nn) saids that C holds in every case where
M is ai, since we have a proof for each case.
17 / 41

18. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Example I: Bottom Type
The first example of enumeration types is the bottom type, the
type representing absurdity. Absurdity is understood as a
proposition which has no proof, which is straightforwardly
represeted as an enumeration type which is inhabited by no term.
Definition (⊥ type)
⊥
def
≡ {}
Definition (⊥-Formation/Elimination Rules)
⊥ : type
(⊥F)
M : ⊥ C : ⊥ → type
caseM () : C(M)
(⊥E)
18 / 41

19. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
EFQ
The “Ex Falso Quodlibet” (EFQ) rule is straightforwardly derived
from ⊥-Elimination Rule. Thus dependent type theory with
enumeration types of arity 0 is stronger than intuitionistic logic.
Theorem (Ex Falso Quodlibet)
M : ⊥ C : type
caseM () : C
(EFQ)
Proof.
M : ⊥
C : type x : ⊥
1
C : type
(WK)
λx.C : ⊥ → type
(→I ),1
caseM () : (λx.C)M ( β C)
(⊥E)
19 / 41

20. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Negation
By using ⊥, the negation of A (notation: ¬A) is defined as
follows:
Definition (¬)
¬A
def
≡ A → ⊥
20 / 41

21. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Example: Inferences that require EFQ
Susan or Mary killed John. Mary didn’t kill John.
=
⇐
Susan killed John.
u : kill(s, j ) kill(m, j ), v : ¬kill(m, j ) kill(s, j ) true
u : kill(s, j ) kill(m, j ) x : kill(s, j )
1
x : kill(m, j )
1
v : ¬kill(m, j )
vx : ⊥
(→E)
casevx() : kill(s, j )
(EFQ)
case u of (λx.x; λx.casevx()) : kill(s, j )
( E),1
21 / 41

22. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Example II: Top Type
The second example of enumeration types is the top type, the type
representing necessary truth. Necessary truth is understood as a
proposition that there is always a proof (), called an unit.
Definition ( type)
def
≡ {()}
Definition ( -Formation Rule)
: type
( F)
() :
( I )
M : C : → type N : C()
caseM (N) : C(M)
( E)
22 / 41

23. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Example III: Finite model
Suppse that entity
def
≡ {mary, susan, john}. Under the
signature: σ
def
≡ girl : entity → type,
smart : entity → type,
mg : girl(mary),
sg : girl(susan),
jg : ¬girl(john),
ms : smart(mary),
ss : smart(susan),
js : ¬smart(john)
the following inference holds:
(x:entity) → girl(x) → smart(x) true
(i.e. “Every girl is smart.”)
23 / 41

24. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
A proof of “Every girl is smart.”
x : {mary, susan, john}
1
ms : smart(mary)
(CON )
y : girl(mary)
2
ms : smart(mary)
(WK)
λy.ms : girl(mary) → smart(mary)
(→I ),2
ss : smart(susan)
(CON )
y : girl(susan)
2
ss : smart(susan)
(WK)
λy.ss : girl(susan) → smart(susan)
(→I ),2
x : girl(john)
3
gs : ¬girl(john)
(CON )
gs(x) : ⊥
(→I )
....
smart(john) : type
casegs(x)() : smart(john)
(⊥E
λx.(casegs(x)()) : girl(john) → smart(john)
(→I ),3
case(λy.ms, λy.ss, λx.(casegs(x)())) : girl(x) → smart(x)
({}E),1
λx.case(λy.ms, λy.ss, λx.(casegs(x)())) : (x:entity) → girl(x) → smart(x)
(ΠI ),1
24 / 41

25. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Summary
⊥ and are instances of enumeration types.
Generally, ∃ and ¬∀ propositions can be verified by a single
witness, while ∀ and ¬∃ propositions can be verified only
analytically, if they quantify over possibly infinite domain.
In model-theoretic semantics, even ∀ and ¬∃ propositions can
be shown to be true under some finite model, while it is not
the case in proof-theoretic semantics without enumeration
types.
entity defined in terms of enumeration types behaves as finite
models, enables us to mimic model-theoretic semantics.
25 / 41

26. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Natural Number Type
26 / 41

27. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Natural Numbers
Definition (N-Formation Rules)
N : type
(NF)
The type N is defined by the constructor 0 (zero) and s (the
successor function).
Definition (N-Introduction Rules)
0 : N
(NI )
n : N
s(n) : N
(NI )
(NI ) also serves as the introduction rule for s. The digits are
defined in the following way: 1
def
≡ s0, 2
def
≡ ss0, 3
def
≡ sss0, . . .
27 / 41

28. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Natural Numbers
The (NE) rule is the elimination rule of N (and the formulation
rule of the natrec constructor).
Definition (N-Elimination Rules)
n : N C : N → type e : C(0)
x : N....
i
y : C(x)
....
i
M : C(s(x))
natrec(n, e, λx.λy.M) : C(n)
(NE),i
Intuitively, the (NE) rule corresponds to the mathematical
induction. where e is a proof for 0 and f is a proof for s(n).
Definition (β-reduction rules (one-step))
natrec(0, e, f) →β e
natrec(s(n), e, f) →β f(n)(natrec(n, e, f))
28 / 41

29. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Addition and Multiplication
The addition operator “+” and the multiplication operator “·” for
nutural numbers illustrate the use of the natrec constructor.
Definition (Addition and Multiplication)
m + n
def
≡ natrec(m, n, λx.λy.s(y))
m · n
def
≡ natrec(m, 0, λx.λy.(y + x))
Exercise: Proove the following theorems:
Theorem
m : N n : N
m + n : N
(+F)
m : N n : N
m · n : N
(·F)
29 / 41

30. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Example of Addition
2 + 1
≡ s s 0 + s0
→β natrec(s s 0 , s0, λx.λy.s(y))
→β (λx.λy.s(y))( s 0 )(natrec( s 0 , s0, λx.λy.s(y)))
β s(natrec( s 0 , s0, λx.λy.s(y))
→β s(λx.λy.s(y))( 0 )(natrec( 0 , s0, λx.λy.s(y)))
→β ss(natrec( 0 , s0, λx.λy.s(y)))
→β sss0
≡ 3
m + n
def
≡ natrec(m, n, λx.λy.s(y))
natrec(0, e, f) →β e
natrec(s( n ), e, f) →β f( n )(natrec( n , e, f)) 30 / 41

31. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Exercises on natural numbers
Prove the following theorems:
Theorem
0 + n β n
0 · n β 0
Theorem
1 + 1 β 2
Theorem
sn =β 1 + n
s(m) + n =β s(m + n)
s(m) · n =β (m · n) + n
31 / 41

32. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Finite Sequences
32 / 41

33. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Finite Sequences
The disjoint union type, the enumeration types, and the natural
number type enable us to define a series of types known as finite
sequences (Aczel (1980))
Definition (Finite Sequence)
M(n)
def
≡ natrec(n, ⊥, λx.λy.(y ))
33 / 41

34. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Finite Sequences
Then, M(0), M(1), M(2), . . . are respectively defined as types
which inhabits 0, 1, 2, . . . canonical terms, as follows.
M(0) = natrec(0, ⊥, λx.λy.(y ))
= ⊥
M(s0) = natrec(s0, ⊥, λx.λy.(y ))
= (λx.λy.(x ))(0)(natrec(0, ⊥, λx.λy.(y )))
= ⊥
M(ss0) = natrec(ss0, ⊥, λx.λy.(y ))
= (λx.λy.(y ))(s0)(natrec(s0, ⊥, λx.λy.(y )))
= (λx.λy.(y ))(s0)(⊥ )
= (⊥ )
. . .
34 / 41

35. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Finite Sequences
M0 is equivalent to ⊥, thus inhabits no term.
M(s0) only inhabits a term ι2().
M(ss0) inhabits two terms ι1ι2() and ι2().
. . .
Exercise
Show that:
ι1ι2() : M(ss0)
ι2() : M(ss0)
35 / 41

36. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Intensional Equality type
36 / 41

37. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Extended Syntax
A collection of Preterms for an extended theory is augmented with
three terms: Λ =Λ Λ (intensional types), reflΛ(Λ) (proof terms
for the reflexive laws), idpeel(Λ, Λ) (proof terms for )
Definition (Preterms)
A collection of preterms (notation: Λ) for an alphabet
(Var, Con) is recursively defined by the following BNF notation:
Λ := x | c | type | kind
| (x:Λ) → Λ | λx.Λ | ΛΛ
|
x:Λ
Λ
| (Λ, Λ) | π1(Λ) | π2(Λ)
| Λ =Λ Λ | reflΛ(Λ) | idpeel(Λ, Λ)
where x ∈ Var and c ∈ Con.
37 / 41

38. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Typing Rules
Definition (Id-Formation Rules)
A : s M : A N : A
M =A N : type
(IdF)
Definition (Id-Introduction Rule)
A : type M : A
reflA(M) : M =A M
(IdI )
Definition (Id-Elimination Rules)
E : M1 =A M2 C : (x:A) → (y:A) → (x =A y) → type N : (x:A) → Cxx(reflA(x))
idpeel(e, N) : CM1M2E
(IdE)
38 / 41

39. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Reduction
Definition (Reduction for Id)
idpeel(reflA(M), N) →β N(M)
39 / 41

40. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Theorems of Id-type
Theorem (Symmetry law for Id)
A : type M =A N true
N =A M true
Theorem (Transitivity law for Id)
A : type L : A M : A N : A L =A M true M =A N true
L =A N true
Theorem (Substitution by Id)
A : type M : A N : A P : A → type M =A N true P M true
P N true
40 / 41

41. References
Reference I
Aczel, P. H. (1980) “Frege structures and the notions of
proposition truth and set”, In: J. Barwise, H. J. Keisler, and K.
Kunen (eds.): The Kleene Symposium. Amsterdam, North-
Holland Publishing Company, pp.31–59.
Elbourne, P. (2011) Meaning: A Slim Guide to Semantics. Oxford
University Press.
Ranta, A. (1994) Type-Theoretical Grammar. Oxford University
Press.
41 / 41