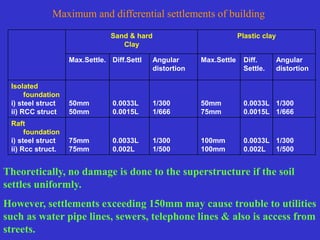
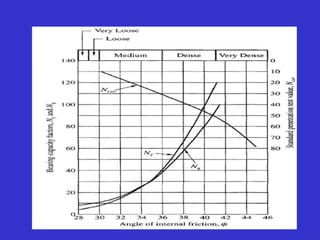
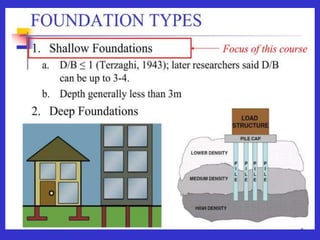
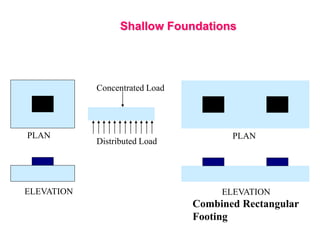
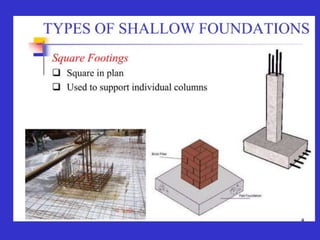
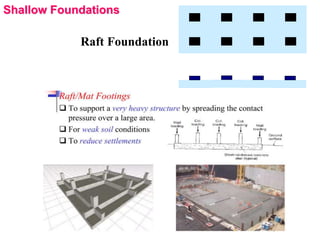
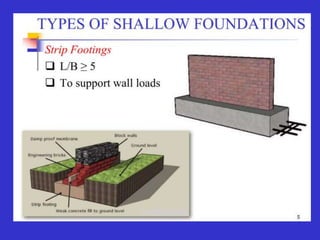
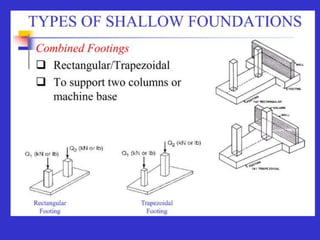
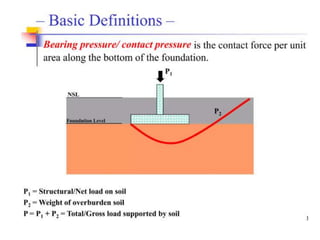
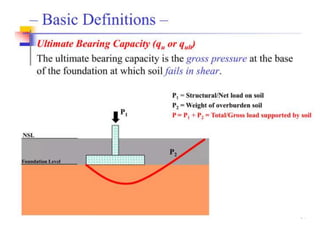
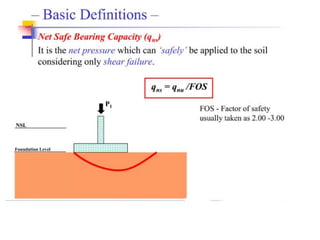
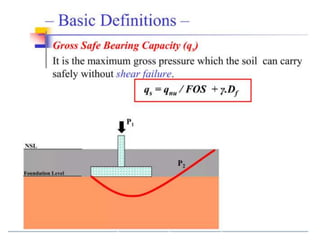
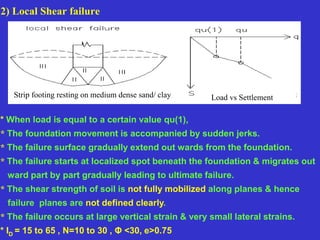
This document provides information on shallow foundations, including raft foundations. It discusses the bearing capacity of shallow foundations and factors that influence it, such as soil type, water table level, and loading conditions. Equations for calculating ultimate bearing capacity are presented, including Terzaghi's bearing capacity equation. The document also covers settlement of foundations, differential settlement, and allowable settlement values.

1. Bearing Capacity of Shallow Foundation
Sudheer Kr. J
AP, CE

6. Shallow Foundations
PLAN
ELEVATION ELEVATION
PLAN
Combined Rectangular
Footing
Distributed Load
Concentrated Load

8. Shallow Foundations
Raft Foundation

9. Raft or Mat Foundation
Raft or Mat foundations:
• It is used where other shallow or
pile foundations are not suitable.
• It is also recommended in
situations where the bearing
capacity of the soil is inadequate,
• The load of the structure is to be
distributed over a large area,
• The structure is subjected
continuously to shocks or jerks.
• the whole basement floor slab acts
as the foundation.
• The total load of the structure is
spread evenly over the entire area
of the structure

10. Raft foundations are economic when:
• The soil is weak and the load has to be spread over a large
area.
• The structure includes a basement.
• Columns are closely placed.
• Other kinds of foundations are not feasible.
• Differential settlement is to be prevented.

13. Why a Foundation is Provided?
• Foundation should fulfill the following objectives:
• Distribute the weight of the structure over a large area of
soil.
• Avoid unequal settlement.
• Prevent the lateral movement of the structure.
• Increase structural stability.
Why There are Different Types of Footing?
As we know that
1. there are different types of soil,
2. bearing capacity of the soil is different for each type of soil.3.
3. Depending on the soil profile, size, and load of the structure,
engineers chose different kinds of foundations.

14. Bearing Capacity Of Shallow Foundation
* A foundation is required for distributing
the loads of the superstructure on a large
area.
* The foundation should be designed
such that
a) The soil below does not fail in shear &
b) Settlement is within the safe limits.

22. Basic Definitions :
1) Ultimate Bearing Capacity (qu) :
The ultimate bearing capacity is the
gross pressure at the base of the
foundation at which soil fails in shear.
2) Net ultimate Bearing Capacity (qnu) :
It is the net increase in pressure at the
base of foundation that cause shear failure
of the soil.
Thus, qnu = qu – γDf (ovrbruden pressure)

23. 3) Net Safe Bearing Capacity (qns) :
It is the net soil pressure which can be
safely applied to the soil considering only shear
failure.
Thus, qns = qnu /FOS
FOS - Factor of safety usually taken as 2.00 -3.00
4) Gross Safe Bearing Capacity (qs) :
It is the maximum pressure which the soil can
carry safely without shear failure.
qs = qnu / FOS + γ Df

24. 5)Net Safe Settlement Pressure (qnp) :
It is the net pressure which the soil can
carry without exceeding allowable
settlement.
6) Net Allowable Bearing Pressure (qna ):
It is the net bearing pressure which can be
used for design of foundation.
Thus,
qna = qns ; if qnp > qns
qna = qnp ; if qns > qnp
It is also known as Allowable Soil Pressure
(ASP).

25. Modes of shear Failure :
Vesic (1973) classified shear failure of soil under a
foundation base into three categories depending on
the type of soil & location of foundation.
1) General Shear failure.
2) Local Shear failure.
3) Punching Shear failure

26. General Shear failure –
Strip footing resting on surface Load –settlement curve
of dense sand or stiff clay
* The load - Settlement curve in case of footing resting on surface of dense sand
or stiff clays shows pronounced peak & failure occurs at very small stain.
* A loaded base on such soils sinks or tilts suddenly in to the ground showing a
surface heave of adjoining soil
* The shearing strength is fully mobilized all along the slip surface & hence
failure planes are well defined.
* The failure occurs at very small vertical strains accompanied by large lateral
strains.
* ID > 65 ,N>35, Φ > 360, e < 0.55

27. 2) Local Shear failure
* When load is equal to a certain value qu(1),
* The foundation movement is accompanied by sudden jerks.
* The failure surface gradually extend out wards from the foundation.
* The failure starts at localized spot beneath the foundation & migrates out
ward part by part gradually leading to ultimate failure.
* The shear strength of soil is not fully mobilized along planes & hence
failure planes are not defined clearly.
* The failure occurs at large vertical strain & very small lateral strains.
* ID = 15 to 65 , N=10 to 30 , Φ <30, e>0.75
Strip footing resting on medium dense sand/ clay Load vs Settlement

28. 3) Punching Share failure
* The loaded base sinks into soil like a punch.
* The failure surface do not extend up to the ground surface.
* No heave is observed.
* Large vertical strains are involved with practically no lateral
deformation.
* Failure planes are difficult to locate

30. Terzaghi’s Method
• Assumptions of Terzaghi’s bearing capacity method:
1. Depth of foundation is less than or equal to its width
2. No sliding occurs between foundation and soil
3. Soil beneath foundation is homogeneous semi infinite mass
4. Mohr-Coulomb model for soil
5. General shear failure mode is the governing mode
6. Soil above the foundation base has no shear failure
7. No applied moment present
8. It is applied to strip/ continuous footing

31. Terzaghi’s Bearing Capacity Analysis –
Terzaghi (1943) analyzed a shallow continuous footing by
making some assumptions –

33. * The failure zones do not extend above the horizontal plane
passing through base of footing
* The failure occurs when the down ward pressure exerted by
loads on the soil adjoining the inclined surfaces on soil wedge is
equal to upward pressure.
* Downward forces are due to the load (=qu× B) & the weight of
soil wedge (1/4 γB2 tanØ)
* Upward forces are the vertical components of resultant passive
pressure (Pp) & the cohesion (c’) acting along the inclined
surfaces.

35. For equilibrium:
ΣFv = 0
1 γ B2tan ø + quxB = 2Pp +2C’ × Li sinø’
4
where Li = length of inclined surface CB
( = B/2 /cosø’)
Therefore,
qu× B = 2Pp + BC’ tanø’ - ¼ γ B2tanø’ –------ (1)
The resultant passive pressure (Pp) on the surface
CB & CA constitutes three components ie. (Pp)r,
(Pp)c & (Pp) q,
Thus,
Pp = (Pp)r + (Pp)c + (Pp)q

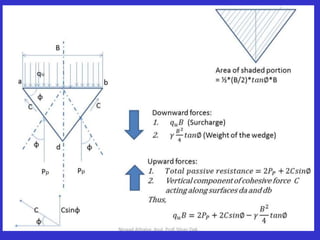
36. qu× B= 2[ (Pp)r +(Pp)c +(Pp)q ]+ Bc’tanø’-¼ γ B2 tanø’
Substituting; 2 (Pp)r - ¼rB2tanø1 = B × ½ γ BNr
2 (Pp)q = B × γ D Nq
& 2 (Pp)c + Bc1 tanø1 = B × C1 Nc;
We get,
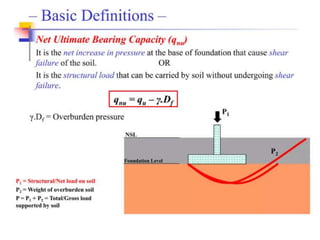
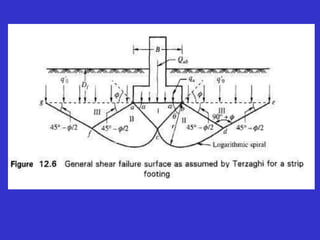
qu = C’Nc + γ Df Nq + 0.5 γ B N γ
This is Terzaghi’s Bearing capacity equation for
determining ultimate bearing capacity of strip footing.
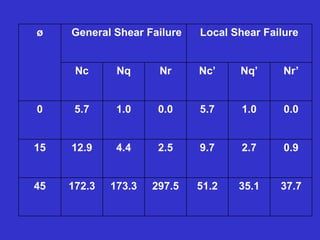
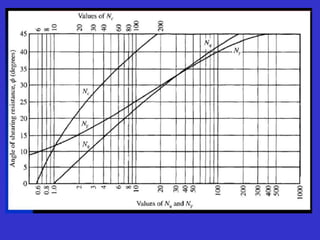
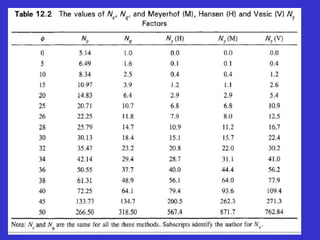
Where Nc, Nq & Nr are Terzaghi’s bearing capacity
factors & depends on angle of shearing resistance (ø)

39. ø General Shear Failure Local Shear Failure
Nc Nq Nr Nc’ Nq’ Nr’
0 5.7 1.0 0.0 5.7 1.0 0.0
15 12.9 4.4 2.5 9.7 2.7 0.9
45 172.3 173.3 297.5 51.2 35.1 37.7

41. Important points :
* Terzaghi’s Bearing Capacity equation is applicable
for general shear failure.
* Terzaghi has suggested following empirical reduction to
actual c & ø in case of local shear failure
Mobilised cohesion Cm = 2/3 C
Mobilised angle of øm = tan –1 (⅔tanø)
Thus, Nc’,Nq’ & Nr’ are B.C. factors for local shear failure
qu = CmNc’+ γ Df Nq’+ 0.5 γ B Nr’
* Ultimate Bearing Capacity for square & Circular footing -Based
on the experimental results, Terzaghi’s suggested following
equations for UBC –
Square footing qu = 1.2c’ Nc + γ Df Nq + 0.4 γ BNr
Circular footing qu = 1.2c1Nc + γ Df Nq + 0.3 γ BNr

43. Effect of water table on Bearing Capacity :
* The equation for ultimate bearing capacity by Terzaghi
has been developed based on assumption that water table is
located at a great depth .
* If the water table is located close to foundation ; the
equation needs modification.

44. i) When water table is located above the base of footing -
*
The effective surcharge is reduced as the effective weight below
water table is equal to submerged unit weight.
q = Dw.r +x.γsub
put x = Df-Dw
q = γsub Df +( γ- γsub)Dw

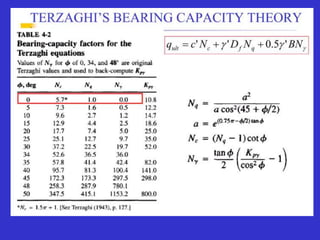
45. Thus,
qu = c’Nc + [γsub Df +(γ - γsub )Dw] Nq + 0.5 γsub BNr
When, Dw =0
qu =c’Nc + γsub Nc + 0.5 γsub BNr
& when x = 0
qu = c’Nc + γ Df Nq + 0.5 γsub BNr

46. ii) When water table is located at depth y below base :
* Surcharge term is not affected.
* Unit weight in term is gavg = gsub + y ( g – gsub)
B
Thus,
qu = c’Nc + γ Df Nq + 0.5B γavg Nr
When y = B ; W.T. at B below base of footing.
qu = c’Nc + γ Df Nq + 0.5 B γ Nr
Hence when ground water table is at y ≥ B, the equation is not
affected.

47. Hansen’s Bearing Capacity Equation :
Hansen’s Bearing capacity equation is :
qu = cNcScdcic + qNqSqdqiq + 0.5 γ BNrSrdr ir
where,
Nc,Nq, & Nr are Hansen’s B.C factors which are some
what smaller than Terzaghi’s B.C. factors.
Sc.Sq &Sr = shape factors which are independent of
angle of shearing resistance
dc,dq, & dr = depth factors
Ic, iq & ir = inclination factors

50. The same form of equation has been adopted by I.S. 6403 –1971 &
may be used for general form as
qnu = c Nc Sc dc ic + q(Nq-1) Sqdqiq + 0.5 γ B Nr Srdr ir W’
I. S Method

56. PLATE LOAD TEST HYPER LINK

60. Plate load test results
Double Tangent method

62. Advantages of Plate Load Test
• Being able to understand the foundation behavior under
loading conditions.
• Evaluation of bearing capacity of soil at a certain depth and
prediction of settlement for a certain load.
• Shallow foundation can be calculated considering the allowable
bearing capacity, which can be predicted from the plate load
test.
• Time and cost-efficient.
• Easy to perform.
• Reliable.

63. Limitations of Plate Load Test
• The test predicts the behavior of soil located at a depth less than
twice the depth of the width of the bearing plate. But in practical
condition, the influence zone of a foundation is up to a much greater
depth.
• The plate load test is performed for a short time period, so it cannot
predict the settlement for a longer period, especially for cohesive
soil.
• The bearing capacity for clayey soil is almost similar to the bearing
capacity obtained from the plate load test, but in the case of dense
sandy soil, the plate load test provides a conservative value. The
actual capacity obtained for dense sandy soil is higher than the
results from the plate load test.
• The settlement for losing sandy soil is usually greater than the
settlement indicated by the plate bearing test.

65. Settlement of foundation :
a) Settlement under loads
Settlement of foundation can be classified as-
1. Elastic settlement (Si): Elastic or immediate
settlement takes place during or immediately after
the construction of the structure. It is also known as
the distortion settlement as it is due to distortions
within foundation soil.
2. Consolidation settlement (Sc): Consolidation
settlement occurs due to gradual expulsion of water
from the voids at the soil. It is determined using
Terzaghi's theory of consolidation.
3. Secondary consolidation settlement (Ss): The
settlement occurs after completion of the primary
consolidation. The secondary consolidation is non-
significant for inorganic soils.

66. Thus,
Total settlement (s) = Si+ Sc + Ss
b) Settlement due to other causes
1. Structural collapse of soil.
2. Underground erosion.
3. Lowering of water table. .
4. Thermal changes.
5. Subsidence etc.

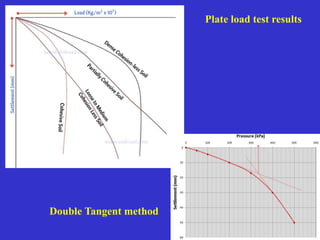
67. Elastic settlement of foundation :
a) On Cohesive soils
According to schleicher, the vertical settlement
under uniformly distributed flexible area is,
Si = q B 1- μ2/Es I
where
q -uniformly distributed load.
B - characteristic length of loaded area,
Es - modulus of elasticity of the soil.
μ - poisson's ratio.
I - influence factor which dependent upon
elastic properties of base & shape at base.
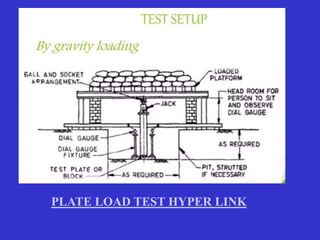
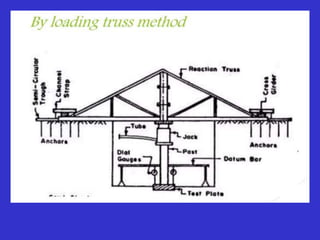
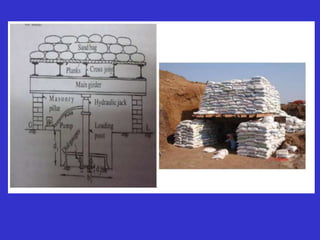
Alternatively, the value of [1- μ2/Es] I can be
determined from the plate load test.

68. b) On Cohesionless Soils
According to Stuartmann & Hartman immediate settlement
on Cohesionless soils is given by -
Where, C1 - Correction factor for depth of foundation
embedment
C2 - correction factor for creep is soils.
q - pressure at the level of foundation
q - surcharge (γ Df)
Es- modulus of elasticity = 766 N (KN/m2) from SPT
= 2qc from SCPT
  




ZB
Z S
i
E
I
q
q
C
C
S
0
2
2
1

69. Settlement of foundation on Cohesionless Soils
Settlement of foundations on Cohesionless soils are
generally determined indirectly using the semi-empirical
methods.
1. Static Cone Penetration method
In this, the sand layer is divided into small layers such
that each small layer has approximately constant value
of the cone resistance. The average value of the cone
resistance of each small layer is determined.
The settlement of each layer is determined using the
following equation-
S = H/C Log (σ0 + Δ σ) / σ0
Where, c = 1.5 qc/ σ0

70. in which qC - static cone resistance
σ0 - mean effective overburden pressure,
Δ σ - Increase is pressure at center of layer
due to net foundation pressure.
H - thickness of layer.
The total settlement of the entire layer is
equal to the sum of settlements of individual layers.
2. Standard Penetration Test
IS 8009 (part I) 1976 gives a chart for the calculation of
settlement per unit pressure as a foundation of the width
of footing & the standard penetration number.
3. Plate Load Test
The settlement of the footing can be determined from
the settlement of the plate in the plate load test.

71. Differential Settlement
The difference between the magnitudes of settlements at any two
points is known as differential settlement.
* If there is large differential settlement between various part of a
structure, distortion may occur due to additional moments
developed.
* The differential settlement may caused due to tilting of a rigid
base, dishing of flexible base or due to non uniformity of loading.
* If S1 & S2 are the settlements at two points,then differential
settlement is
 = S1 -S2
Angular distortion = (S1- S2 ) / L =  /L
*

72. * It is difficult to predict the differential settlement.
* It is generally observed indirectly from the maximum
settlement.
* It is observed that the differential settlement is less
than 50% of the maximum settlement is most of the
cases.
The differential settlement can be reduced by providing
rigid rafts, founding the structures at great depth &
avoiding the eccentric loading.

73. Allowable Settlement
* The allowable maximum settlement depends upon
the type of soil, the type of foundation & the
structural framing system.
* The maximum settlement ranging from 20mm to
300mm is generally permitted for various
structures.
* IS 1904-1978 gives values of the maximum &
differential settlements of different type of building.

74. Sand & hard
Clay
Plastic clay
Max.Settle. Diff.Settl Angular
distortion
Max.Settle Diff.
Settle.
Angular
distortion
Isolated
foundation
i) steel struct
ii) RCC struct
50mm
50mm
0.0033L
0.0015L
1/300
1/666
50mm
75mm
0.0033L
0.0015L
1/300
1/666
Raft
foundation
i) steel struct
ii) Rcc struct.
75mm
75mm
0.0033L
0.002L
1/300
1/500
100mm
100mm
0.0033L
0.002L
1/300
1/500
Theoretically, no damage is done to the superstructure if the soil
settles uniformly.
However, settlements exceeding 150mm may cause trouble to utilities
such as water pipe lines, sewers, telephone lines & also is access from
streets.
Maximum and differential settlements of building

75. Bearing capacity of granular soil based on standard penetration test
value

77. OK

78. https://www.slideshare.net/sameerthaiyam1/pile-foundation-
87349854