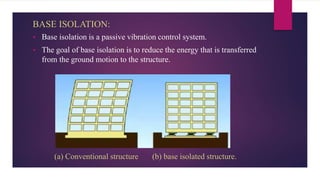
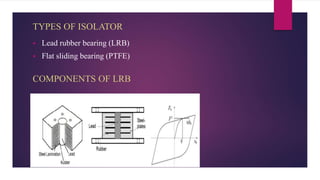
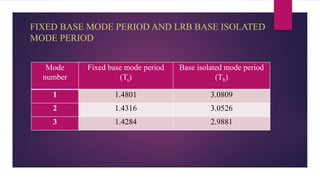
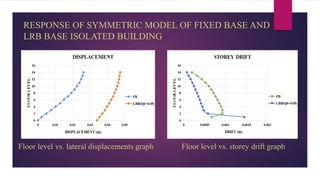
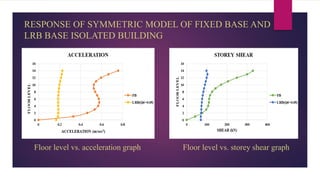
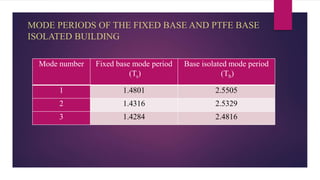
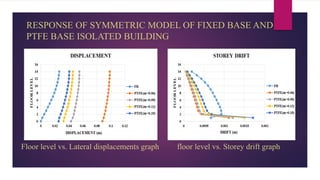
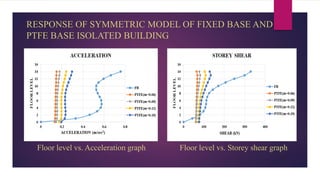
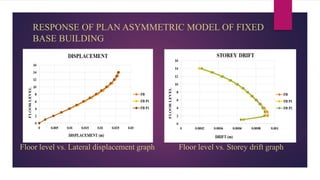
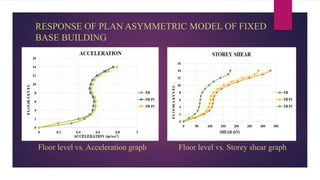
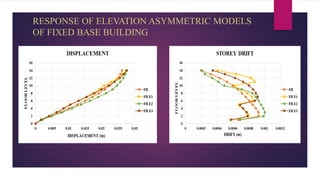
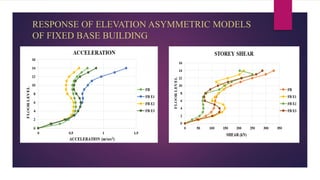
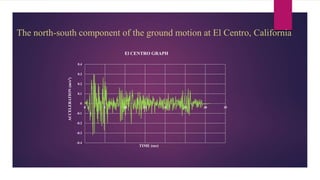
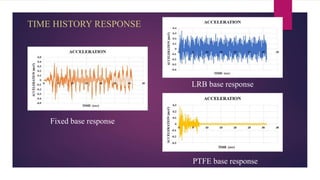
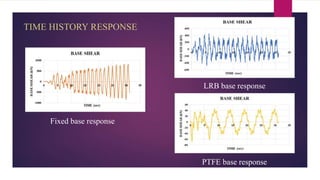
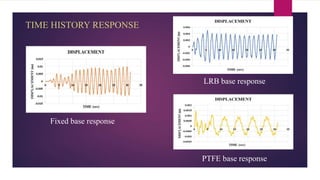
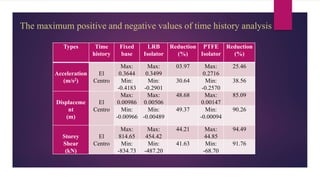
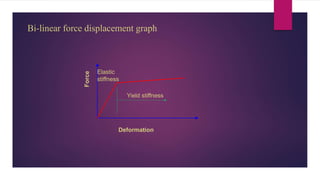
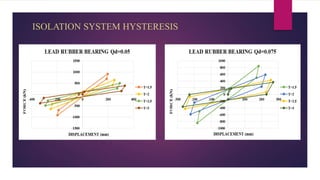
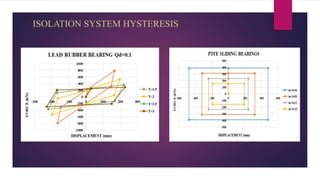
The document discusses the dynamic response of a 14-storey reinforced concrete frame building using base isolators. It aims to analyze the response of the building with and without base isolators, including lead rubber bearings and sliding bearings, under earthquake ground motions. The analysis is performed using the finite element software ETABS. The results show that base isolation is effective at reducing seismic responses like displacement, acceleration, base shear and storey drift compared to a fixed base building. PTFE isolators provide more reduction than LRB isolators in most responses. Irregularities in building plan and elevation also increase the response of a fixed base building.

1. DYNAMIC RESPONSE OF RC FRAME
BUILDING USING BASE ISOLATORS
GUIDED BY,
B S JAYASHANKAR BABU
ASSOCIATE PROFESSOR,
DEPARTMENT OF CIVIL
ENGINEERING.
PREMKUMAR M K
4th sem, M.Tech,
CAD structures,
PESCE.

2. INTRODUCTION
 Earthquakes cause inertia forces proportional to the product of the building
mass and the ground accelerations.
 Due to this mass asymmetry in building center of mass is shifted from
center of stiffness causing eccentricity. As this eccentricity increases, torsion
in building also increases.
 As the ground accelerations increases, the strength of the building must be
increased to avoid structural damage.
 It is not practical to continue to increase the strength of the building
indefinitely.
 Base isolation is one of the most widely accepted techniques to protect
structures and to mitigate the risk to life and property from strong
earthquakes.

3. OBJECTIVES
 To find out the response of 14 storey RC bare frame with and without base
isolator (i.e., Mode period, displacement, acceleration, base shear, storey
drift) by response spectrum analysis. Numerical modelling and analysis are
carried out using finite element based software ETABS.
 To study the response of base isolated building using lead rubber bearing
and sliding bearing system for bare frame of symmetric model using time
history analysis of El Centro earthquake data.
 To compare the performance of RC bare frame having plan and elevation
irregularities with and without base isolator.
 Study of isolation system variations and isolation system hysteresis in case
of lead rubber bearing (LRB) and PTFE system.

4. LITERATURE REVIEW
Bill Robinson et al. (1993), have written a book called seismic isolation for
designers and structural engineers. This book gives total insight into the
practical methods of construction of seismically isolated buildings. The
different types of isolation devices and their properties are discussed here.
W h Robinson (1997), describes the principles of seismic isolation and discuss
some of the isolation systems available before giving some examples of the
application of seismic isolation to structure in new Zealand.
M Kikuchi and S Kamamato (2007), presents an analytical model for lead-
rubber bearing to predict bearing force-displacement behavior under extremely
large deformations.

5. LITERATURE REVIEW
Kaab mohamed zohair (2011), presented the use of the base isolation device
LRB (lead rubber bearing) allows the control of the deformation which are
localized on this last, and also allows carrying out a satisfactory compromise
between the reduction of the seismic forces and the increase in the
deformations of the base isolation.
Kelly et al., studied the effectiveness of seismic base isolation in controlling
the deformations in prefabricated concrete structures. When utilized in
prefabricated concrete structures seismic base isolation has the potential to
reduce the ductility demand from these structures under seismic loading.

6. BASE ISOLATION:
 Base isolation is a passive vibration control system.
 The goal of base isolation is to reduce the energy that is transferred
from the ground motion to the structure.
(a) Conventional structure (b) base isolated structure.

7. THE PURPOSE OF BASE ISOLATION
 As for all the load cases encountered in the design process, such as
gravity and wind, should work to meet a single basic equation:
CAPACITY > DEMAND.
This can be achieved by,
 Ductility
 Leads to higher floor accelerations.
 Damage to structural components, which may not be repairable.
EFFECTS OF DUCTILITY

8. TYPES OF ISOLATOR
 Lead rubber bearing (LRB)
 Flat sliding bearing (PTFE)
COMPONENTS OF LRB

9. COMPONENTS OF PTFE
FLAT SLIDING ISOLATOR

10. DESIGN OF ISOLATOR
1. A displacement is assumed, using the total rubber thickness as a starting
point.
2. The effective stiffness of the bearing at this displacement is calculated.
3. The effective period is calculated using the total seismic mass and the
effective period.
4. The equivalent viscous damping is calculated from the area of the
hysteresis loop. For HDR, the damping and shear modulus are
interpolated from tabulated values of these quantities versus shear strain.
5. The damping factor, b, is calculated for the equivalent viscous damping.
6. The spectral displacement is calculated from the acceleration response
spectrum at the effective period, modified by the damping factor b.
7. This displacement is compared with the displacement assumed in step 1.
Above. If the difference exceeds a preset tolerance, the calculated
displacement defines a new starting displacement and the procedure is
repeated until convergence is achieved.

11. SYMMETRIC MODEL PLAN

12. DETAILS OF RC FRAME
Number of bays in x-direction = 6 bay
Number of bays in y-direction = 3 bay
Number of storeys = 14 storey (G +13)
Bottom storey = 3.0 m
Other storeys = 3.0 m
Link element = 0.5 m
Beam size = 0.7 m x 0.4 m
Column size = 0.5 m x 0.5 m
Slab thickness = 0.15 m
Live load on the slab = 3 kN /m2

13. NONLINEAR LINK TYPE: LRB ISOLATOR
U1 Linear effective stiffness = 1253000 kN/m
U2 and U3 Linear effective stiffness = 1174 kN/m
U2 and U3 Nonlinear stiffness = 8599 kN/m
U2 and U3 Yield strength = 117 kN
U2 and U3 Post yield stiffness ratio = 0.09

14. NONLINEAR LINK TYPE: PTFE ISOLATOR
U1 Linear effective stiffness = 5000000 kN/m
U1 Nonlinear effective stiffness = 5000000 kN/m
U2 and U3 Linear effective stiffness = 2038 kN/m
U2 and U3 Nonlinear stiffness = 2000000 kN/m
U2 and U3 Friction coefficient, slow = 0.04
U2 and U3 Friction coefficient, fast = 0.06
U2 and U3 Rate parameter = 40
U2 and U3 Radius of sliding surface = 0

15. FIXED BASE MODE PERIOD AND LRB BASE ISOLATED
MODE PERIOD
Mode
number
Fixed base mode period
(Ts)
Base isolated mode period
(Tb)
1 1.4801 3.0809
2 1.4316 3.0526
3 1.4284 2.9881

16. RESPONSE OF SYMMETRIC MODEL OF FIXED BASE AND
LRB BASE ISOLATED BUILDING
Floor level vs. lateral displacements graph Floor level vs. storey drift graph

17. RESPONSE OF SYMMETRIC MODEL OF FIXED BASE AND
LRB BASE ISOLATED BUILDING
Floor level vs. acceleration graph Floor level vs. storey shear graph

18. MODE PERIODS OF THE FIXED BASE AND PTFE BASE
ISOLATED BUILDING
Mode number Fixed base mode period
(Ts)
Base isolated mode period
(Tb)
1 1.4801 2.5505
2 1.4316 2.5329
3 1.4284 2.4816

19. RESPONSE OF SYMMETRIC MODEL OF FIXED BASE AND
PTFE BASE ISOLATED BUILDING
Floor level vs. Lateral displacements graph floor level vs. Storey drift graph

20. RESPONSE OF SYMMETRIC MODEL OF FIXED BASE AND
PTFE BASE ISOLATED BUILDING
Floor level vs. Acceleration graph Floor level vs. Storey shear graph

21. PLAN ASYMMETRY
Plan asymmetric model P1 Plan asymmetric model P2
(2% Eccentricity) (5% Eccentricity)

22. MODE PERIODS OF THE FIXED BASE BUILDING FOR
ASYMMETRIC MODELS (P1 AND P2)
Mode
number
Fixed base FBP1
(Ts)
Fixed base FBP2
(Ts)
1 1.4830 1.4729
2 1.4230 1.3597
3 1.3894 1.2579

23. RESPONSE OF PLAN ASYMMETRIC MODEL OF FIXED
BASE BUILDING
Floor level vs. Lateral displacement graph Floor level vs. Storey drift graph

24. RESPONSE OF PLAN ASYMMETRIC MODEL OF FIXED
BASE BUILDING
Floor level vs. Acceleration graph Floor level vs. Storey shear graph

25. ELEVATION ASYMMETRY
Asymmetric model (E1) Asymmetric Model (E2) Asymmetric model (E3)

26. RESPONSE OF ELEVATION ASYMMETRIC MODELS
OF FIXED BASE BUILDING

27. RESPONSE OF ELEVATION ASYMMETRIC MODELS
OF FIXED BASE BUILDING

28. The north-south component of the ground motion at El Centro, California
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0 5 10 15 20 25 30 35
ACCELERATION(m/s2)
TIME (sec)
El CENTRO GRAPH

29. TIME HISTORY RESPONSE
Fixed base response
LRB base response
PTFE base response

30. TIME HISTORY RESPONSE
Fixed base response
LRB base response
PTFE base response

31. TIME HISTORY RESPONSE
Fixed base response
LRB base response
PTFE base response

32. The maximum positive and negative values of time history analysis
Types Time
history
Fixed
base
LRB
Isolator
Reduction
(%)
PTFE
Isolator
Reduction
(%)
Acceleration
(m/s2)
El
Centro
Max:
0.3644
Max:
0.3499
03.97 Max:
0.2716
25.46
Min:
-0.4183
Min:
-0.2901
30.64 Min:
-0.2570
38.56
Displaceme
nt
(m)
El
Centro
Max:
0.00986
Max:
0.00506
48.68 Max:
0.00147
85.09
Min:
-0.00966
Min:
-0.00489
49.37 Min:
-0.00094
90.26
Storey
Shear
(kN)
El
Centro
Max:
814.65
Max:
454.42
44.21 Max:
44.85
94.49
Min:
-834.73
Min:
-487.20
41.63 Min:
-68.70
91.76

33. Isolation system variation for LRB and PTFE bearings

34. Bi-linear force displacement graph
Elastic
stiffness
Yield stiffness
Deformation

35. ISOLATION SYSTEM HYSTERESIS

36. ISOLATION SYSTEM HYSTERESIS

37. FUTURE SCOPE OF STUDY
 The study on optimal base isolation system of multistory RC frame
buildings in a probabilistic sense.
 Study on laminated rubber bearing constructed with scrap tires filled
crushed rock as bearing to reduce manufacturing costs.
 With recent advancement in material technology, more study can be
focused on material qualities used in isolators like their strength,
durability, high vertical stiffness, low horizontal stiffness and high energy
dissipating capacity.

38. CONCLUSIONS
 Natural period of the structure increases in case of base isolated building in
comparison with fixed base building
 Base isolation reduces the seismic response of plan and vertical irregular
models
 Base shear, acceleration, storey drift decreases whereas generally lateral
displacement increases in base isolated building.
 Fixed base buildings have zero storey acceleration at base of building
whereas, in case of base isolated building appreciable amount of storey
acceleration will been found out at base.
 In case of PTFE base isolated building, reduction in response is more for
=0.06 rather than =0.15.

39.  In case of PTFE base isolated building, reduction in response is more for =0.06
rather than =0.15.
 PTFE isolator alone cannot be used in a building because it has no restoring
force in the system and results in large lateral displacement
 Lead rubber bearing effectively reduces 70% of the base shear in the building.
 In case of LRB isolation system variations, with increase in time period
displacement and damping of the system increases.
 In case of PTFE isolation system variations, with increase in time period
displacement increases. Damping remains constant for all values of time period.

40. REFERENCES
 Ivan skinner, R., Trevor E. Kelly and bill robinson, W. H. (1993), A text
book on seismic isolation for designers and structural engineers, robinson
seismic limited, holmes consulting group.
 W. H. Robinson (1998), “passive control of structures, new zealand
experience”, ISET, journal of earthquake technology.
 Kelly et al. Uasge of seismic base isolation to reduce the ductility demand
from prefabricated concrete structure, holmes consulting group limited.
 Trevor e kelly, s. E. (2001), design guidelines on base isolation of
structures, holmes consulting group, new zealand.
 Pankaj agarwal and manish shirkhande. (2010), A text book on earthquake
resistant design of structures, PHI learning private limited, new delhi.
 Anil k. Chopra, dynamic of structures, theory and application to
earthquake engineering, third edition.
 Wai-fah chen charles scawthorn, “earthquake engineering handbook”.

42. ISOLATOR INSTALLATION IN
BUILDING

43. Thank you