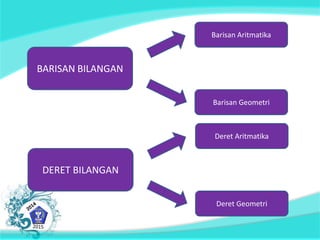
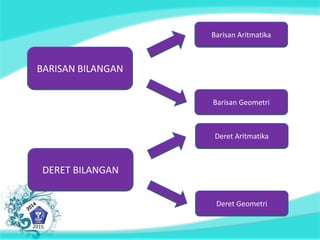
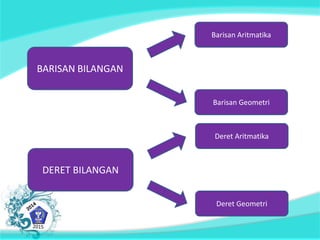
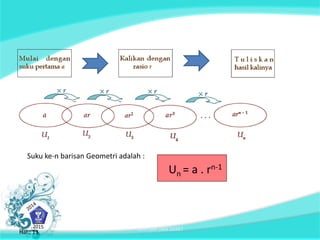
Dokumen ini membahas tentang konsep barisan dan deret tak hingga, termasuk barisan aritmatika dan geometri serta rumus yang digunakan untuk menentukan suku-suku dalam barisan tersebut. Ada penekanan pada kemampuan siswa dalam menerapkan strategi penyelesaian masalah matematika dan sikap disiplin serta tanggung jawab. Selain itu, dokumen juga menyajikan contoh soal terkait barisan dan deret.

1. BARISAN DAN DERET
TAK HINGGA

3. KOMPETENSI DASAR
1.1 Menghayati dan mengamalkan ajaran agama yang dianutnya
2.1 Memilliki motivasi internal, kemampuan bekerjasama, konsisten,
sikap disiplin, rasa percaya diri, dan sikap toleransi dalam
perbedaan strategi berpikir dalam memilih dan menerapkan
strategi menyelesaikan masalah
2.2 Mampu mentranformasi diri dalam berperilaku jujur, tangguh
menghadapi masalah, kritis, dan disiplin dalam mengerjakan tugas
matematika
2.3 menunjukan sikap bertanggungjawab, rasa ingin tahu, jujur dan
perilaku peduli lingkungan
3.9 Mendeskripsikan konsep barisan tak hingga sebagai fungsi dengan
daerah asal himpunan bilangan asli
4.5 Menerapkan konsep barisan dan deret tak hingga dalam
penyelesaian masalah sederhana

4. BARISAN DAN
DERET BILANGAN

5. BARISAN BILANGAN
Barisan Aritmatika
Barisan Geometri
DERET BILANGAN
Deret Aritmatika
Deret Geometri

6. Barisan Bilangan
Barisan bilangan adalah bilangan-bilangan yang dituliskan secara terurut
dengan aturan tertentu.Aturan tersebut digunakan untuk menentukan suku-suku
dari barisan.Aturan tersebut dapat ditulisakan dalam bentuk rumus fungsi
Un dengan domain bilangan asli.Misalkan barisan bilangan segitiga berikut.
1 3 6 10
dst

7. Secara umum rumus suku ke-n dapat dituliskan :
Un = n(n+1).
Rumus Un = n(n + 1) merupakan fungsi dengan
domain bilangan asli, yaitu 1,2,3,4,5,6,7,….
Nilai suku ke-p dari barisan bilangan tersebut
sama dengan nilai fungsi Un untuk n = p, yaitu Up
Misalkan nilai suku ke-15 dapat ditentukan
sebagai berikut.
U15 = (15) (15+1) = (15)(16) =120

8. BARISAN BILANGAN
Barisan Aritmatika
Barisan Geometri
DERET BILANGAN
Deret Aritmatika
Deret Geometri

9. BARISAN ARITMATIKA
• Bilangan-bilangan berurutan seperti pada speedometer memiliki selisih yang
sama untuk setiap dua suku berurutannya sehingga membentuk suatu barisan
bilangan
• Barisan Aritmatika adalah suatu barisan dengan selisih (beda) dua suku yang
berurutan selalu tetap
a a + b a + 2b a + 3b …. a + (n-1)b
Hal.: 9 BARISAN DAN DERET Hal.: 9

10. CONTOH SOAL
Hal.: 10 BARISAN DAN DERET Hal.: 10

11. BARISAN BILANGAN
Barisan Aritmatika
Barisan Geometri
DERET BILANGAN
Deret Aritmatika
Deret Geometri

12. BARISAN DAN DERET GEOMETRI
Barisan geometri adalah suatu barisan dengan pembanding
(rasio) antara dua suku yang berurutan selalu tetap.
Ada selembar kertas biru, akan dipotong-potong menjadi dua bagian.
Hal.: 12 BARISAN DAN DERET Hal.: 12

13. Suku ke-n barisan Geometri adalah :
Un = a . rn-1
Hal.: 13 BARISAN DAN DERET Hal.: 13

14. CONTOH SOAL

15. BARISAN BILANGAN
Barisan Aritmatika
Barisan Geometri
DERET BILANGAN
Deret Aritmatika
Deret Geometri

16. DERET BILANGAN

17. BARISAN BILANGAN
Barisan Aritmatika
Barisan Geometri
DERET BILANGAN
Deret Aritmatika
Deret Geometri

18. DERET ARITMATIKA
Hal.: 18 BARISAN DAN DERET Hal.: 18

19. BARISAN BILANGAN
Barisan Aritmatika
Barisan Geometri
DERET BILANGAN
Deret Aritmatika
Deret Geometri

20. DERET GEOMETRI
Hal.: 20 BARISAN DAN DERET Hal.: 20

21. DERET TAK
HINGGA

22. Hal.: 22 BARISAN DAN DERET Hal.: 22