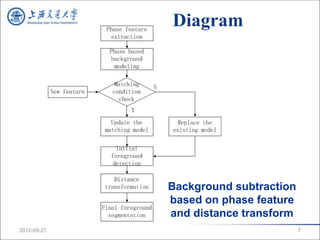
This document summarizes a research paper on background subtraction under sudden illumination changes. It proposes using phase features and distance transforms. Key points: 1. It extracts phase features from Gabor wavelet coefficients that are insensitive to illumination changes. 2. It models pixel backgrounds using Gaussian mixtures on the phase space and updates the models under a novel matching condition. 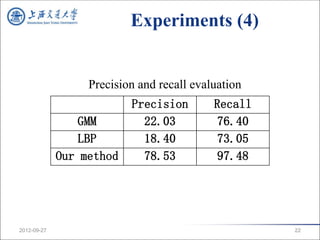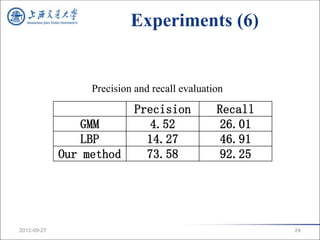3. Experiments show the method achieves better precision and recall than GMM and LBP methods on test sequences under illumination changes.

1. Background Subtraction Based on Phase and Distance
Transform Under Sudden Illumination Change
Authors: Gengjian Xue, Jun Sun, Li Song
Reporter: Li Song
Shanghai Jiao Tong University
2012-09-27 1

2. Outline
Introduction
Background subtraction based on phase
feature and distance transform
Experimental results
Conclusion
2012-09-27 2

3. Introduction (1)
Moving object detection is an active
research subject in computer vision.
Foreground detection under sudden
illumination change is still a challenging
problem.
2012-09-27 3

4. Introduction (2)
Parametric density estimation technique
Gaussian Mixture Models (GMM), C.Stauffer and
Grimson, CVPR, 1999.
Nonparametric density estimation technique
Kernel Density Estimation (KDE), A. Elgammal,
etc., Pro.IEEE, 2002.
Region-based technique
Local Binary Pattern based (LBP), M.Heikkila and
M. Pietikainen, TPAMI, 2006
2012-09-27 4

5. Introduction (3)
Other methods
Wallflower system, K.Toyama, etc., ICCV, 1999
Pixel order information based, Binglong Xie, etc.,
Image Vision Computing, 2004
Pilet’s method, ECCV 2008.
---a statistical model combing two texture-based
features and the ratios of the current image to the
background image in each color channel
2012-09-27 5

6. Motivation
Phase is insensitive to illumination
change.
The basic framework of GMM method.
Blob aggregation using distance
transform.
2012-09-27 6

7. Diagram
Background subtraction
based on phase feature
and distance transform
2012-09-27 7

8. Phase feature extraction (1)
The Gabor wavelet coefficient:
G , ( z )  A , z ( z )  exp(i  ,v ( z ))
A ,v ( z ) :amplitude item
  , ( z ) [0,2 ) :phase item
Each pixel has max  max wavelet coefficients
2012-09-27 8

9. Phase feature extraction (2)
Phase extraction principle:
The larger amplitude of the coefficient is, the
more efficient the coefficient represents the pixel
information and the more discriminative of the
corresponding phase is.
Multiple phase extraction reasons:
rotation property
range of single phase is small
2012-09-27 9

10. Phase feature extraction (3)
The phase feature is defined:
L
p( z )   i ( z )
i 1
p(z ) : the phase feature
 i (z ) : the Gabor phase corresponding to the ith largest Gabor
amplitude of the pixel
L : the number of phase to be extracted
N  N image subdivision
2012-09-27 10

11. Background modeling
K mixture of Gaussian distributions
In the background modeling stage, each pixel is modeled
independently by a mixture of Gaussian distributions
where each Gaussian represents the phase distribution.
kth Gaussian distribution represented by
 k ,  and  k , total weights   i  1
K
2
k
i 1
2012-09-27 11

12. Model updating (1)
Set L  3, p( z ) [0,6 )
Singular regions exists, matching condition
is in different expressions
 6  k  X t  2.5 k if X t   and 6  k  

 6  k  X t  2.5 k if  k   and 6  X t  
 X    2.5 others
 t k k
2012-09-27 12

13. Model updating (2)
Condition satisfied
1. if  k   and 6  X t  
  k   k   ( X t   k  6 )
 2
 k  (1   ) k2   ( X t   k  6 ) 2
2. if X t   and 6  k  
  k   k   ( X t   k  6 )
 2
 k  (1   ) k2   ( X t   k  6 ) 2
3. Others
 k  k   ( X t  k )
 2
 k  (1   ) k2   ( X t   k ) 2
2012-09-27 13

14. Model updating (3)
Weights update k  (1   )k  M k
 k is beyond [0,6 )
 k   k  6 if  k  6

 k   k  6 if  k  0
Condition not satisfied
New Gaussian replace   X t ,    init , low init
2012-09-27 14

15. Foreground detection
Sorted in  
Background distributions:
b
B  arg min( k  T )
k 1
2012-09-27 15

16. Distance transform (1)
Initial detection result
2012-09-27 16

17. Distance transform (2)
Euclidean distance transform of pixel a(i, j )
d (i, j )  min (i  x) 2  ( j  y) 2
( x , y )W
2012-09-27 17

18. Blob aggregation
Example results before and after blob aggregation
2012-09-27 18

19. Experiments (1)
Several sequences for testing.
GMM and LBP methods are employed for
comparison.
Visual and numerical evaluation are used
Precision and Recall as the metrics.
TP TP
Precision   100% Recall   100%
TP  FP TP  FN
2012-09-27 19

20. Experiments (2)
Parameter selection
Gabor filter:  max  4 max  6
Phase extraction: N  4, L  3
Gaussian model: K  3, Tb  0.7
Segment value for DT: Td  1.2
2012-09-27 20

21. Experiments (3)
（a） （b） （c）
（d） （e） （f）
GMM LBP Our
2012-09-27 21

22. Experiments (4)
Precision and recall evaluation
Precision Recall
GMM 22.03 76.40
LBP 18.40 73.05
Our method 78.53 97.48
2012-09-27 22

23. Experiments (5)
（a） （b） （c）
（d） （e） （f）
GMM LBP Our
2012-09-27 23

24. Experiments (6)
Precision and recall evaluation
Precision Recall
GMM 4.52 26.01
LBP 14.27 46.91
Our method 73.58 92.25
2012-09-27 24

25. Conclusions
Pixel phase as feature.
Novel matching condition and updating
scheme.
Distance transform on the initial
detection results.
2012-09-27 25