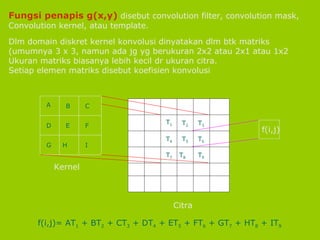
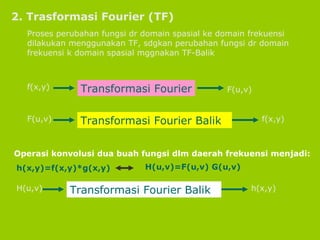
Dokumen ini menjelaskan konsep konvolusi dan transformasi Fourier dalam pengolahan citra, terutama dalam manipulasi citra dalam domain frekuensi. Proses konvolusi melibatkan operasi pengalihan citra dengan kernel dan dapat memperbaiki kualitas, menghilangkan derau, dan mendeteksi tepi. Transformasi Fourier digunakan untuk menganalisis frekuensi citra dan mempercepat perhitungan konvolusi melalui pengalihan ke domain frekuensi.

1. IV. KONVOLUSI & TRANSFORMASI FOURIER (TF) Konvolusi terdpt pd operasi pengolahan citra yg mengalikan sebuah citra dgn mask atau kernel Transformasi Fourier dilakukan bila citra dimanipulasi dlm domain frekuensi 1. Konvolusi pd Fungsi 2D Operasi konvolusi didefinisikan sbb: a. Fungsi kontinyu b. Fungsi diskret

2. Fungsi penapis g(x,y) disebut convolution filter, convolution mask, Convolution kernel, atau template. Dlm domain diskret kernel konvolusi dinyatakan dlm btk matriks (umumnya 3 x 3, namun ada jg yg berukuran 2x2 atau 2x1 atau 1x2 Ukuran matriks biasanya lebih kecil dr ukuran citra. Setiap elemen matriks disebut koefisien konvolusi T 1 T 2 T 4 T 8 T 7 T 3 T 6 T 5 T 9 A B D H G C F E I Kernel Citra f(i,j) f(i,j)= AT 1 + BT 2 + CT 3 + DT 4 + ET 5 + FT 6 + GT 7 + HT 8 + IT 9

3. Contoh: Citra f(x,y) berukuran 5x5 dan sebuah kernel ukuran 3x3 sbb: Lakukan operasi konvolusi antara citra f(x,y) dgn kernel g(x,y) f(x,y)*g(x,y)= ??????? f(x,y) = 4 3 5 4 6 6 5 5 2 5 6 6 6 2 6 7 5 5 3 3 5 2 4 4 g(x,y)= 0 -1 0 -1 4 -1 0 -1 0 Posisi (0,0) dr kernel

4. Pixel-pixel pinggir diabaikan, tdk dikonvolusi (tetap). Duplikasi elemen citra, misalnya elemen kolom pertama disalin ke kolom M+1, begitu sebaliknya. Elemen kosong diasumsikan 0. Catatan: Ada masalah untuk pinggiran citra, hal ini dpt diatasi dgn cara: Dpt dilihat bhw operasi konvolusi merupakan komputasi pd aras lokal, krn komputasi utk suatu pixel pd citra keluaran melibatkan pixel-pixel tetangga pd citra masukannya. Konvolusi berguna pd proses pengolahan citra al: Perbaikan kualitas citra Penghilangan derau Penghalusan/pelembutan citra Deteksi tepi, penajaman tepi dll Contoh: lakukan konvolusi suatu citra foto hitam putih Anda dgn penapis Gaussian utk mempertajam tepi-tepi di dlm citra. Penapis Gaussian adalah sebuah mask berukuran 3x3

5. Operasi konvolusi dilakukan perpixel & untuk setiap pixel dilakukan operasi perkalian dan penjumlahan, shg memerlukan komputasi yg besar. Jk citra berukuran NxN & kernel mxm, mk jumlah perkalian dlm orde N 2 m 2 Contoh: jk citra 512x512 & kernel 16x16 mk ada sekitar 32juta perkalian, tdk cocok untuk proses real time. Suatu cara mengurangi wkt komputasi adalah mentransformasi citra dan kernel ke dlm domain frekuensi dlm hal ini Transf. Fourier Keuntungan penggunaan domain frekuensi adalah proses konvolusi dpt diterapkan dlm btk perkalian langsung. g(x,y)= 1 2 1 2 4 2 1 2 1

6. 2. Trasformasi Fourier (TF) Proses perubahan fungsi dr domain spasial ke domain frekuensi dilakukan menggunakan TF, sdgkan perubahan fungsi dr domain frekuensi k domain spasial mggnakan TF-Balik Operasi konvolusi dua buah fungsi dlm daerah frekuensi menjadi: f(x,y) Transformasi Fourier F(u,v) F(u,v) Transformasi Fourier Balik f(x,y) h(x,y)=f(x,y)*g(x,y) H(u,v)=F(u,v) G(u,v) H(u,v) Transformasi Fourier Balik h(x,y)

7. Intisari TF : menguraikan sinyal atau gelombang menjd sejumlah sinusoida dr berbagai frekuensi, yg jumlahnya ekivalen dgn gel asal. Dlm pengolahan citra, TF digunakan untuk menganalisis frekuensi pd operasi seperti perekaman citra, perbaikan kualitas citra, restorasi citra, pengkodean dll. Dr analisis frekuensi, dpt dilakukan prubahan frekuensi pd gambar. Perubahan frekuensi berhub dgn spektrum antara gambar yg kabur kontrasnya sampai gambar yg kaya akan rincian visualnya

8. Trasformasi Fourier Diskret Pd pengolahan sinyal dgn komputer digital, fungsi dinyatakan dgn himpunan berhingga nilai diskret. Bila f(x) fungsi kontinyu dibuat diskret dgn N buah sampling sejarak ∆x, Yaitu himpunan nilai {f(x 0 ), f(x 0 +∆x), f(x 0 +2∆x), …,f(x 0 +(N-1)∆x)} Shg f x =f(x 0 +x ∆x), x= 0, 1, 2, …, N-1 Pasangan TF diskret untuk fungsi dgn 1 variabel:

9. Dgn pers Euler, pasangan TF Diskret dpt ditulis: Interpretasi dari TFD adalah sbb: TFD mengkonversi data diskret menjd sejumlah sinusoida diskret yg frekuensinya dinomori dgn u=0, 1, 2, …, N-1 dan amplitudonya F u

10. Contoh: diketahui sinyal f(t) dgn hasil sampling ke dlm nilai-nilai diskret sbb (N=4): x 0 =0.5, f 0 =2 x 1 =0.75, f 1 =3 x 2 =1.0, f 2 =3 x 3 =1.25, f 3 =3 TFD:

11. Spektrum Fouriernya:

12. Citra digital adalah fungsi diskret dlm domain spasial, dgn dua variabel, x dan y. Fungsi diskret dgn 2 variabel dan berukuran N x M, pasangan TFD: atau Untuk u,x = 0, 1, 2, …, N-1 dan v,y=0, 1, 2, …, M-1

13. Algoritma TFD dan balikannya dpt diterapkan untuk fungsi diskret 2D. Mula-mula transformasi dilakukan dlm arah x (nilai y tetap), kemudian hasilnya ditransformasikan lagi dlm arah y Algoritma TFD tdk bagus untuk N yg besar krn komputasinya butuh waktu lama. Kompleksitas wkt algoritma utk TFD N 2 Algoritma cepat utk menghitung TFD adalah FFT yg kompleksitas wktx N 2 log N Untuk N=50. TFC kira-kira 10 kali lebih cepat dr pd TFD