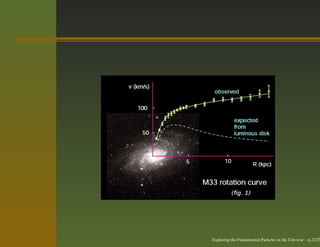
The document discusses exploring fundamental particles in the universe. It begins with an overview of the Standard Model of Particle Physics and theories beyond the Standard Model, such as Grand Unified Theories and supersymmetry. It then discusses how particle physics relates to and helps explain phenomena in astrophysics and cosmology, including neutrino oscillations, dark matter, and the matter-antimatter asymmetry observed in the universe. The document emphasizes the links between problems in particle physics and cosmology.

1. Exploring the Fundamental Particles
in the Universe
Exploring the Fundamental Particles in the Universe – p.1/29

2. Outline
Standard Model of Particle Physics
Beyond the Standard Model
Astroparticle Physics
Exploring the Fundamental Particles in the Universe – p.2/29

3. Standard Model of Particle Physics
LEP T ON S : e − e+ µ− µ+ τ− τ+
¯ ¯
νe νe νµ νµ ντ ¯
ντ
QU ARKS : u ¯
u d ¯
d s ¯
s
c ¯
c b ¯
b t ¯
t
GAU GEBOSON S : γ W ± Z g(8) G
HIGGSBOSON : φ
Antiparticle - same mass, opposite charge Exploring the Fundamental Particles in the Universe – p.3/29

4. PARTICLE DISCOVERIES
Cathode Ray Tube Electron (1897)
Compton scattering expt Photon (1923)
Cosmic Rays Positron (1932), Muon (1936)
Beta decay Electron neutrino (1956)
(nuclear reactors)
Exploring the Fundamental Particles in the Universe – p.4/29

5. ACCELERATORS
FERMILAB p¯
p
KEK e + e−
CERN(LHC) pp
BROOKHAVEN HeavyIonCollisions
Exploring the Fundamental Particles in the Universe – p.5/29

6. CERN - [27km, 100m, 11K rev/s, 1011 p per bunch]
Exploring the Fundamental Particles in the Universe – p.6/29

7. The LHC tunnel
Exploring the Fundamental Particles in the Universe – p.7/29

8. Exploring the Fundamental Particles in the Universe – p.8/29

9. Decaying Higgs after a p-p collision
600mill/s
Exploring the Fundamental Particles in the Universe – p.9/29

10. PARTICLE DISCOVERIES
Accelerators Muon and Tau neutrino, Tau lepton
Up and Down quarks
s,c,b,t quarks
Gluons, W ± , Z (1962-2000)
Exploring the Fundamental Particles in the Universe – p.10/29

11. PARTICLE DISCOVERIES
Accelerators Muon and Tau neutrino, Tau lepton
Up and Down quarks
s,c,b,t quarks
Gluons, W ± , Z (1962-2000)
Higgs particle is not yet discovered. (LHC?)
Exploring the Fundamental Particles in the Universe – p.10/29

12. Theoretical Calculations
Quantum Mechanics Non-relativistic particles
Quantum Field Theory Relativistic particles
Represent each particle by a field
As in QM, work with a Hamiltonian (or Lagrangian)
Use perturbation theory (like in QM) to calculate how
particles decay, interact with each other, etc.
Compare theoretical and experimental results
Exploring the Fundamental Particles in the Universe – p.11/29

13. The Lagrangian of the Standard Model
1 i iµν 1 µν 1 j jµν θ2 g2 ˜
L = − Wµν W − Bµν B − Gµν G + 2
Tr Gj Gjµν
µν
4 4 4 16π
¯ γ µ (1 − γ5 ) i∂µ − g 1 τ i W i − g Y Bµ − gs 1 λj Gj fD
+f D µ µ
2 2 2
¯γ µ (1 + γ5 ) i∂µ − g Y Bµ − gs 1 λj Gj f
+f µ
2 2
2
1 Y 1
+ i∂µ − g τ i Wµ − g Bµ − gs λj Gj φ − V (φ)
i
µ
2 2 2
¯ ¯
−mf φf1 f1 − mf φc f2 f2 [i = 1, 2, 3; j = 1, 2, .., 8]
where f are fermions ( leptons and quarks), Gj , Wµ and
µ
j
Bµ are the strong and electroweak gauge bosons
i
respectively, and φ is the Higgs boson. The Lagrangian
has SU (3)c × SU (2)L × U (1)Y mathematical symmetry,
which spontaneously breaks into SU (3)c × U (1)EM .
Exploring the Fundamental Particles in the Universe – p.12/29

14. Unease with the Standard Model
The Standard Model of Particle Physics has 19
parameters.
The large number of arbitrary parameters in the
Standard Model is a cause of concern.
Exploring the Fundamental Particles in the Universe – p.13/29

15. Unease with the Standard Model
The Standard Model of Particle Physics has 19
parameters.
The large number of arbitrary parameters in the
Standard Model is a cause of concern.
Also neutrinos are massless in the Standard Model.
(1998 - ν mass)
Exploring the Fundamental Particles in the Universe – p.13/29

16. Unease with the Standard Model
The Standard Model of Particle Physics has 19
parameters.
The large number of arbitrary parameters in the
Standard Model is a cause of concern.
Also neutrinos are massless in the Standard Model.
(1998 - ν mass)
Some theoretical calculations of the Higgs mass
make it too large (unless one carefully adjusts
parameters).
Exploring the Fundamental Particles in the Universe – p.13/29

17. Unease with the Standard Model
The Standard Model of Particle Physics has 19
parameters.
The large number of arbitrary parameters in the
Standard Model is a cause of concern.
Also neutrinos are massless in the Standard Model.
(1998 - ν mass)
Some theoretical calculations of the Higgs mass
make it too large (unless one carefully adjusts
parameters).
GO BEYOND THE STANDARD MODEL Exploring the Fundamental Particles in the Universe – p.13/29

18. Beyond the Standard Model
High Energy Theory −→ Standard Model
(like Special Relativity −→ Newtonian Physics)
Exploring the Fundamental Particles in the Universe – p.14/29

19. Beyond the Standard Model
High Energy Theory −→ Standard Model
(like Special Relativity −→ Newtonian Physics)
GRAND UNIFIED THEORIES (GUTs)
(larger mathematical symmetry, neutrino mass)
Exploring the Fundamental Particles in the Universe – p.14/29

20. Beyond the Standard Model
High Energy Theory −→ Standard Model
(like Special Relativity −→ Newtonian Physics)
GRAND UNIFIED THEORIES (GUTs)
(larger mathematical symmetry, neutrino mass)
SUPERSYMMETRY (controls the Higgs mass)
FERMION ←→ BOSON
BOSON ←→ FERMION
γ (PHOTON) ←→ γ (PHOTINO)
˜
e (ELECTRON) ←→ e (SELECTRON)
˜
Exploring the Fundamental Particles in the Universe – p.14/29

21. Beyond the Standard Model
High Energy Theory −→ Standard Model
(like Special Relativity −→ Newtonian Physics)
GRAND UNIFIED THEORIES (GUTs)
(larger mathematical symmetry, neutrino mass)
SUPERSYMMETRY (controls the Higgs mass)
FERMION ←→ BOSON
BOSON ←→ FERMION
γ (PHOTON) ←→ γ (PHOTINO)
˜
e (ELECTRON) ←→ e (SELECTRON)
˜
Discoveries at the LHC? Exploring the Fundamental Particles in the Universe – p.14/29

22. The Standard Model and Beyond
THE STANDARD MODEL OF PARTICLE PHYSICS
Theory: Lagrangian (Quantum Field Theory)
Experiment: Cosmic Rays, Accelerators
BEYOND THE STANDARD MODEL
Grand Unified Theories (GUTs)
Supersymmetry
LARGE HADRON COLLIDER
Exploring the Fundamental Particles in the Universe – p.15/29

23. What about Gravity?
CLASSICAL GRAVITY −− GENERAL THEORY OF RELATIVITY
QUANTUM GRAVITY −− ?
Exploring the Fundamental Particles in the Universe – p.16/29

24. What about Gravity?
CLASSICAL GRAVITY −− GENERAL THEORY OF RELATIVITY
QUANTUM GRAVITY −− ?
SUPERSTRING THEORY
Elementary particles like the photon and the electron are not point-like
objects but are extended objects.
To see the string like behaviour need very high energy probes.
Exploring the Fundamental Particles in the Universe – p.16/29

25. What about Gravity?
CLASSICAL GRAVITY −− GENERAL THEORY OF RELATIVITY
QUANTUM GRAVITY −− ?
SUPERSTRING THEORY
Elementary particles like the photon and the electron are not point-like
objects but are extended objects.
To see the string like behaviour need very high energy probes.
Supersymmetric GUTs are included in superstring theory and the
GRAVITON appears naturally in the particle spectrum. So it is a
UNIFIED QUANTUM THEORY of PARTICLE PHYSICS and GRAVITY.
Exploring the Fundamental Particles in the Universe – p.16/29

26. What about Gravity?
CLASSICAL GRAVITY −− GENERAL THEORY OF RELATIVITY
QUANTUM GRAVITY −− ?
SUPERSTRING THEORY
Elementary particles like the photon and the electron are not point-like
objects but are extended objects.
To see the string like behaviour need very high energy probes.
Supersymmetric GUTs are included in superstring theory and the
GRAVITON appears naturally in the particle spectrum. So it is a
UNIFIED QUANTUM THEORY of PARTICLE PHYSICS and GRAVITY.
d>4 Exploring the Fundamental Particles in the Universe – p.16/29

27. Cosmology and Particle Physics
Particle Physics theories find applications in
astrophysical scenarios and in the context of the Early
Universe. Particularly in the latter case, they allow us to
test interactions of particles at very high energies.
Solar Neutrino Deficit
Dark Matter
Matter-Antimatter Asymmetry
Exploring the Fundamental Particles in the Universe – p.17/29

28. Solar Neutrino Deficit
Nuclear reactions in the Sun
2
p+p → H + e + + νe
p +2 H → 3
He + γ
3
He +3 He → 4
He + 2p
3
He +4 He → 7
Be + γ
7 7
Be + e− → Li + νe
7 8
Be + p → B+γ
8 8
B → Be∗ + e+ + νe
8
Be → 4He +4 He
We detect only 1/3 of the neutrinos νe that we expect.
Exploring the Fundamental Particles in the Universe – p.18/29

29. Neutrino Oscillations
No solution from Solar Physics.
Exploring the Fundamental Particles in the Universe – p.19/29

30. Neutrino Oscillations
No solution from Solar Physics.
Is something happening to neutrinos as they travel from
the sun to the earth?
Exploring the Fundamental Particles in the Universe – p.19/29

31. Neutrino Oscillations
Electron neutrinos emitted by the sun transform into
muon and tau neutrinos. Therefore we detect only 1/3 of
the neutrinos emitted by the sun.
Exploring the Fundamental Particles in the Universe – p.20/29

32. Neutrino Oscillations
Electron neutrinos emitted by the sun transform into
muon and tau neutrinos. Therefore we detect only 1/3 of
the neutrinos emitted by the sun.
This hypothesis of neutrino oscillations has been
confirmed by experiments. (νe ↔ νµ ↔ ντ )
Neutrino oscillations requires neutrino massess
Physics of stars tells us about fundamental particles ν
Exploring the Fundamental Particles in the Universe – p.20/29

33. Dark Matter
Velocity Rotation Curves of Galaxies
Expect v ∼ √ ,
1
r
since v2
mr = G M2 and M is constant.
r
m
BUT ....
Exploring the Fundamental Particles in the Universe – p.21/29

34. Exploring the Fundamental Particles in the Universe – p.22/29

35. Take v ∼ constant. How can this be explained?
Exploring the Fundamental Particles in the Universe – p.23/29

36. Take v ∼ constant. How can this be explained?
v2 Mm
m =G 2
r r
If M (r) = Ar, then v ∼ constant.
Exploring the Fundamental Particles in the Universe – p.23/29

37. Take v ∼ constant. How can this be explained?
v2 Mm
m =G 2
r r
If M (r) = Ar, then v ∼ constant.
But M (r) = Ar ⇒ matter beyond the central luminous
region which we can not see.
This non-luminous matter (does not emit or scatter light)
is called DARK MATTER.
Exploring the Fundamental Particles in the Universe – p.23/29

38. DARK MATTER does not emit or scatter light so it is
difficult to detect.
What is it?
Consists primarily of non-Standard Model matter –
supersymmetric particles, axions, massive neutrinos, ...
High energy physics theories provide possible candidates
for dark matter
Exploring the Fundamental Particles in the Universe – p.24/29

39. Matter-Antimatter Asymmetry
Observed Universe is made up of only matter.
¯
M + M → photons
Antimatter seen in laboratories since 1930s.
We believe that at early times (t < 1s) there were
equal amounts of matter and antimatter in the Universe.
WHERE DID THE ANTIMATTER GO?
Exploring the Fundamental Particles in the Universe – p.25/29

40. Matter-Antimatter Asymmetry
WHERE DID THE ANTIMATTER GO?
Disequilibrium in the early Universe
100 M + 100 M −→ 103 M + 101 M −→ 2 M
Possible mechanism of creating matter excess is via the
decay of GUT bosons X at t ∼ 10−34 s (T ∼ 1026 K).
X −→ M
−→ M
r > r ⇒ N (M ) > N (M ).
¯
Particle physics theories to explain the M-A asymmetry
Exploring the Fundamental Particles in the Universe – p.26/29

41. Conclusion
We have a good understanding of the history and
evolution of our Universe, but there are sill
important outstanding questions – Big Bang, Dark
Matter, Dark Energy
The Standard Model of Particle Physics is good but
not good enough
Need to consider theories Beyond the Standard
Model valid at higher energies
Exploring the Fundamental Particles in the Universe – p.27/29

42. Conclusion
Problems in Particle Physics are often linked to
Cosmology and vice versa
High energy particle physics theories such as String
Theory may explain the Big Bang, Supersymmetric
models may provide the Dark Matter, GUTs may
explain the Matter-Antimatter Asymmetry, Solar
Physics provides clues to the nature of Neutrinos
Accelerators such as the LHC will (hopefully)
discover the dark matter particle
Exploring the Fundamental Particles in the Universe – p.28/29

43. Cosmology and Particle Physics
Books
The First Three Minutes by S. Weinberg
The Big and the Small, vol. I and II by G.
Venkataraman
raghavan@prl.res.in
Exploring the Fundamental Particles in the Universe – p.29/29