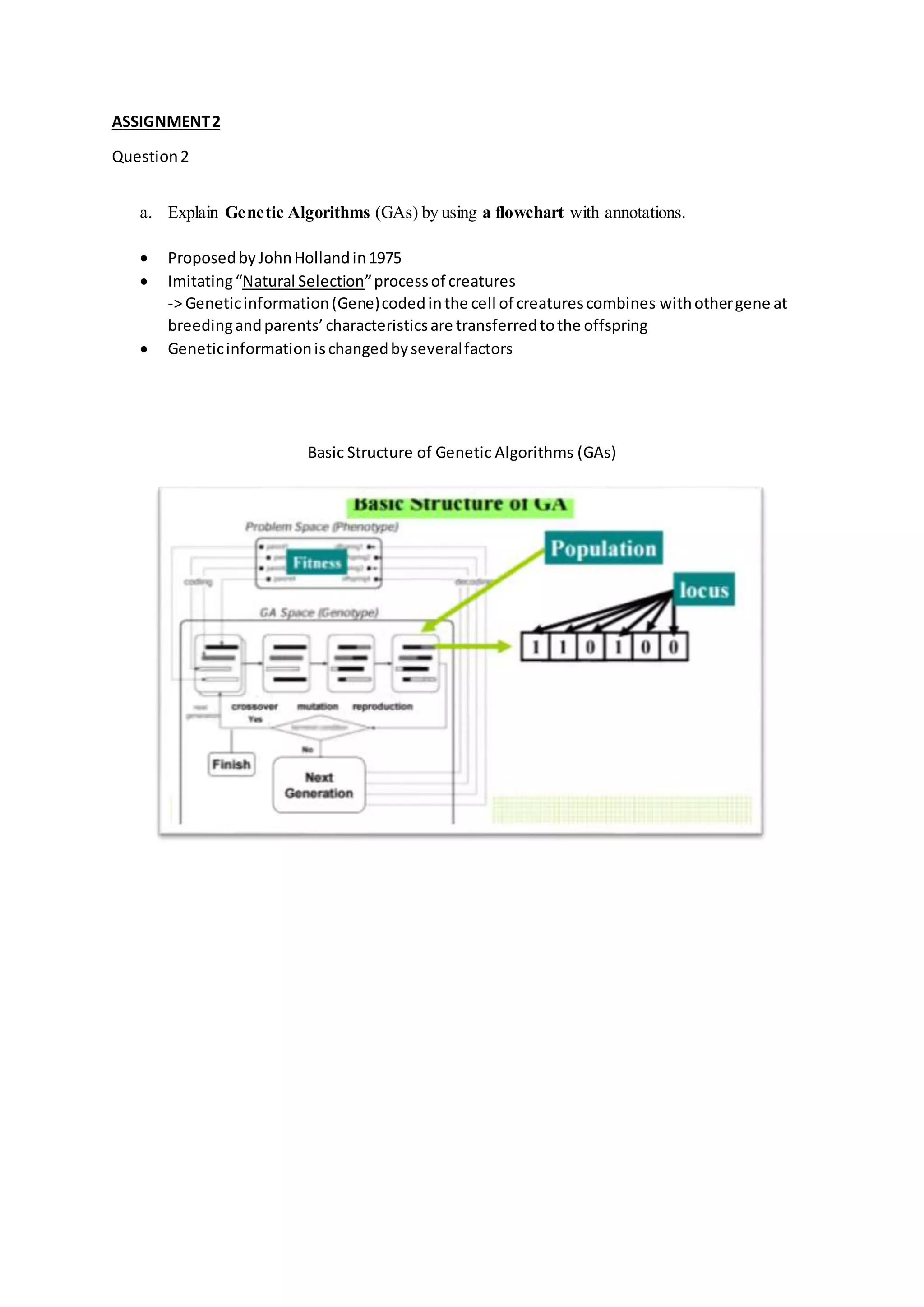
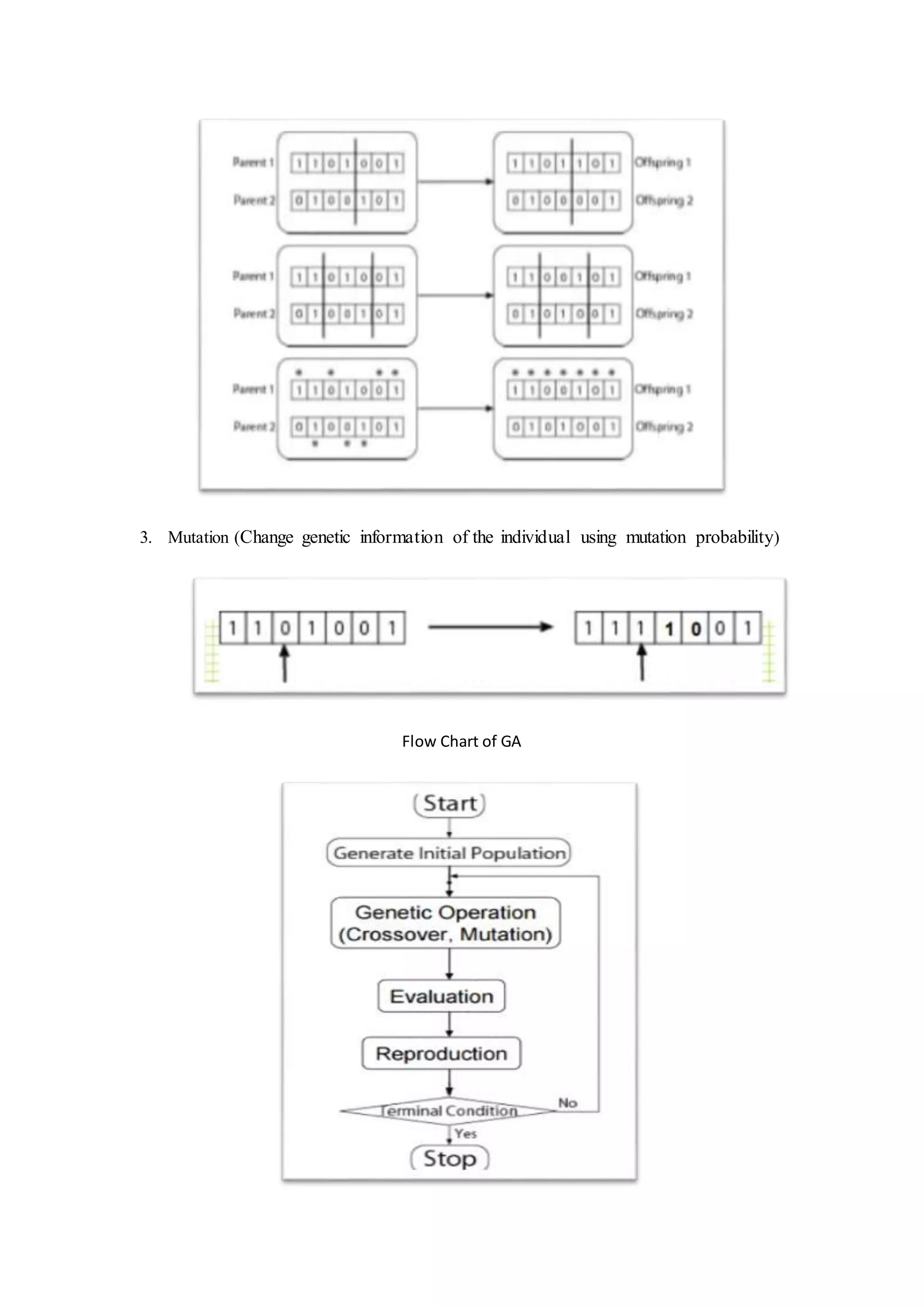
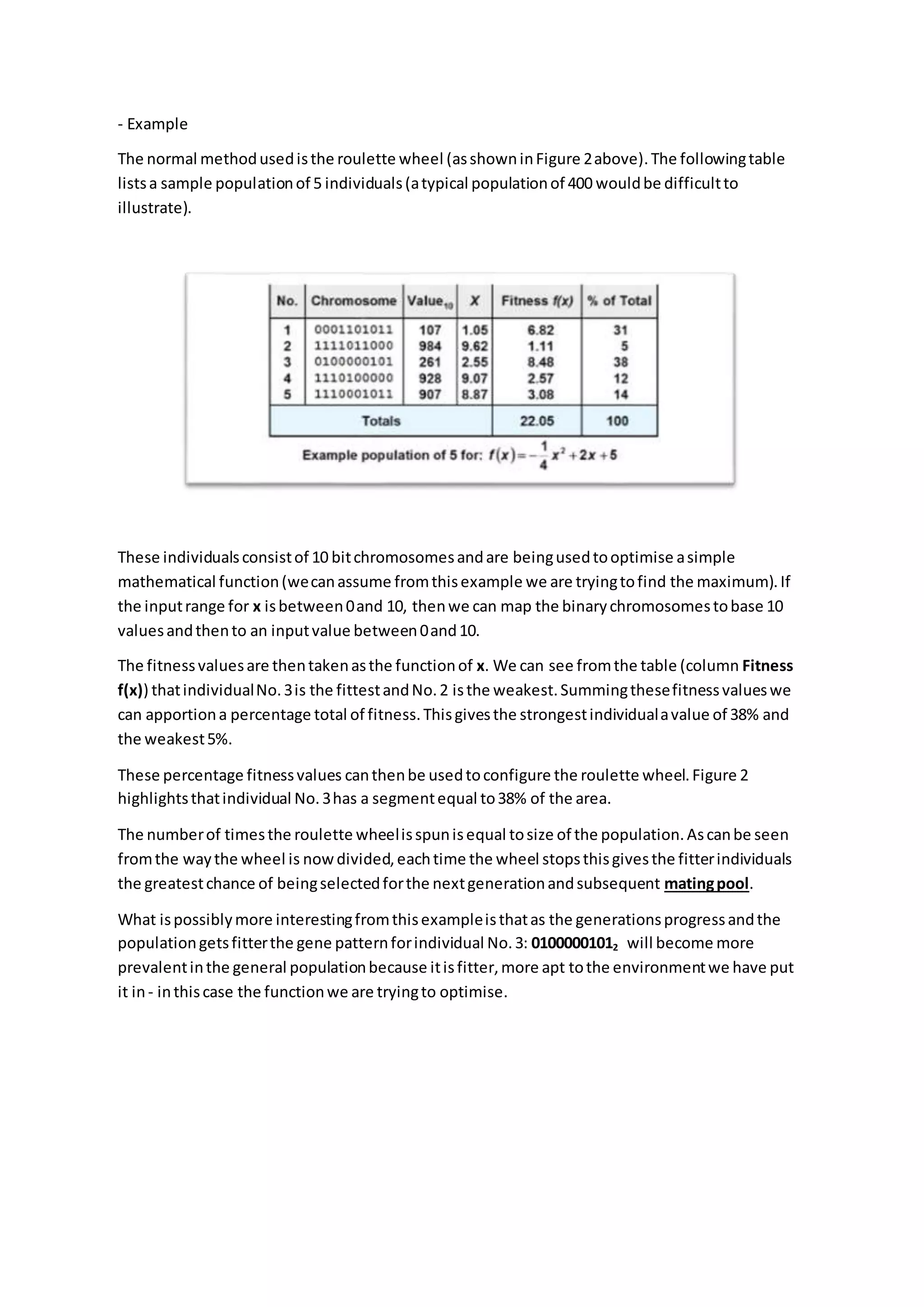
Genetic algorithms imitate natural selection by evolving a population of potential solutions. They use fitness functions to evaluate how close each solution is to the desired outcome. Roulette wheel selection probabilistically selects solutions for reproduction based on their fitness, giving fitter solutions a greater chance of being selected. This process is repeated over multiple generations until an optimal solution emerges.

1. ASSIGNMENT2
Question2
a. Explain Genetic Algorithms (GAs) by using a flowchart with annotations.
 ProposedbyJohnHollandin1975
 Imitating“Natural Selection”processof creatures
-> Geneticinformation(Gene)codedinthe cell of creaturescombines withothergene at
breedingandparents’characteristicsare transferredtothe offspring
 Geneticinformationischangedbyseveralfactors
Basic Structure of Genetic Algorithms (GAs)

2. Genetic Operator of GA
 Genetic operator is the operator for generating new gene based on fitness of each
individual
1. Selection (Selectthe individualsaccordingtotheirfitness)
2. Crossover (Exchange genetic information (0,1) of each parent using crossover
probability)
 One Point Crossover
 Several Points Crossover
 Uniform Crossover

3. 3. Mutation (Change genetic information of the individual using mutation probability)
Flow Chart of GA

4. b. Describe “Roulette Wheel Selection”. Use a diagram to illustrate its use.
- Selectionof the fittest
The basic part of the selectionprocessistostochasticallyselectfromone generationtocreate the
basisof the nextgeneration.The requirementisthatthe fittestindividualshave agreaterchance
of survival thanweakerones.Thisreplicatesnature inthatfitterindividualswilltendtohave a
betterprobabilityof survival andwill goforwardtoformthe mating pool forthe nextgeneration.
Weakerindividuals are notwithoutachance.In nature suchindividualsmayhave geneticcoding
that may prove useful tofuture generations.

5. - Example
The normal methodusedisthe roulette wheel (asshowninFigure 2above).The followingtable
listsa sample populationof 5 individuals(atypical populationof 400 wouldbe difficultto
illustrate).
These individualsconsistof 10 bitchromosomesandare beingusedtooptimise asimple
mathematical function(wecanassume fromthisexample we are tryingtofind the maximum).If
the inputrange for x isbetween0and 10, thenwe can map the binarychromosomestobase 10
valuesandthento an inputvalue between0and10.
The fitnessvaluesare thentakenasthe functionof x. We can see fromthe table (column Fitness
f(x)) thatindividualNo.3is the fittestandNo.2 isthe weakest.Summingthesefitnessvalueswe
can apportiona percentage total of fitness.Thisgivesthe strongestindividualavalue of 38% and
the weakest5%.
These percentage fitnessvalues canthenbe usedtoconfigure the roulette wheel.Figure 2
highlightsthatindividual No.3has a segmentequal to38% of the area.
The numberof timesthe roulette wheelisspunisequal tosize of the population.Ascanbe seen
fromthe waythe wheel is nowdivided,eachtime the wheel stopsthisgivesthe fitterindividuals
the greatestchance of beingselectedforthe nextgenerationandsubsequent matingpool.
What ispossiblymore interestingfromthisexampleisthatas the generationsprogressandthe
populationgetsfitterthe gene patternforindividual No.3: 01000001012 will become more
prevalentinthe general populationbecause itisfitter,more apt tothe environmentwe have put
it in- inthiscase the functionwe are tryingto optimise.

6. c. What is the use of Fitness Functions in GAs?
A fitnessfunctionisaparticulartype of objectivefunction thatisusedtosummarise,asasingle figure
of merit, how close a given design solution is to achieving the set aims.
In particular, in the fields of genetic programming and genetic algorithms, each design solution is
commonly represented as a string of numbers (referred to as a chromosome). After each round of
testing, or simulation, the idea is to delete the 'n' worst design solutions, and to breed 'n' new ones
fromthe bestdesignsolutions.Eachdesignsolution,therefore,needstobe awardedafigure of merit,
to indicate how close it came to meeting the overall specification, and this is generated by applying
the fitness function to the test, or simulation, results obtained from that solution.
The reasonthat geneticalgorithmscannotbe consideredtobe a lazyway of performingdesignwork
is precisely because of the effort involved in designing a workable fitness function.Even though it is
no longerthe humandesigner,butthe computer,thatcomesupwiththe final design,itisthe human
designer who has to design the fitness function. If this is designed badly, the algorithm will either
converge on an inappropriate solution, or will have difficulty converging at all.
Moreover,the fitnessfunctionmustnotonlycorrelate closelywiththe designer'sgoal,itmustalsobe
computed quickly. Speed of execution is very important, as a typical genetic algorithm must be
iterated many times in order to produce a usable result for a non-trivial problem.
Fitness approximation may be appropriate, especially in the following cases:
 Fitness computation time of a single solution is extremely high
 Precise model for fitness computation is missing
 The fitness function is uncertain or noisy.
Two main classes of fitness functions exist: one where the fitness function does not change, as in
optimizingafixedfunctionortestingwithafixedsetof testcases;andone where the fitnessfunction
is mutable, as in niche differentiation or co-evolving the set of test cases.
Anotherwayof lookingat fitnessfunctionsisintermsof a fitnesslandscape,whichshowsthe fitness
for each possible chromosome.
Definition of the fitness function is not straightforward in many cases and often is performed
iterativelyif the fittestsolutionsproducedbyGA are notwhatisdesired.Insome cases,itisveryhard
or impossible to come up even witha guess of what fitness functiondefinition might be. Interactive
genetic algorithms address this difficulty by outsourcing evaluation to external agents (normally
humans).