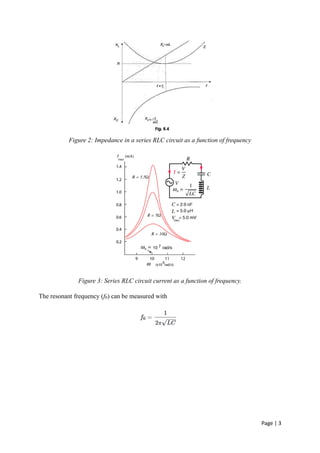
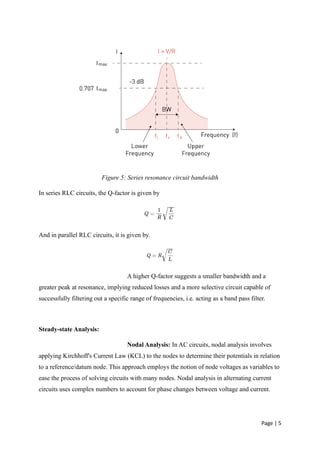
A report on A.C. Circuit Analysis made for MAKAUT (previously WBUT) Continuous Assessment of Basic Electrical Engineering. Circuit analysis, moreover that of alternating current circuits is a crucial subject in Undergraduate level electrical engineering courses. The presentation maybe used as a basic introduction to A.C. circuit analysis in college level courses.

1. A.C. CIRCUIT
ANALYSIS
NAME: AINDRILA HALDAR
ROLL NO: 22
SUBJECT: BASIC ELECTRICAL
ENGINEERING
(ES-EE101)
DEPT.: COMPUTER SCIENCEAND ENGINEERING

2. Page | 1
INTRODUCTION: AC circuit analysis is a method of
studying electrical circuits where the voltage and current fluctuate periodically, typically
following a sinusoidal pattern, allowing engineers to understand how these time-varying
signals interact with circuit components like resistors, capacitors, and inductors, and predict
circuit behavior by utilizing concepts such as phasors and impedance, which simplify
complex calculations related to alternating current (AC) systems.
Resistive, Inductive, and Capacitive Loads Characteristics and behaviour in AC
Circuits:
Resistive Loads: Ohm's law (V = RI) states that there is a
straight relationship between voltage and current for resistive loads, such as heaters and
incandescent light bulbs. The waveforms of an AC circuit rise and fall simultaneously
without phase shifting because the current flowing through a resistor is in phase with the
voltage across it. Real power (P), which is computed as the power used by a resistive load, is
P=V⋅I⋅cos(φ) where φ represents the phase angle of current and voltage. For purely resistive
loads, φ = 0, resulting in a power factor of 1, showing optimum efficiency without reactive
power.
Inductive Loads: Motors, transformers, and coils are
examples of inductive loads that store energy in a magnetic field when current runs through
them. Inductive loads in AC circuits cause the current to lag behind the voltage by 90° (φ =
-90°). This phase shift happens when the inductor opposes changes in current flow, causing a
delay in the current waveform relative to the voltage waveform. The power associated with
inductive loads is primarily reactive power (Q), which does not produce work but oscillates
between source and load. This results in a power factor less than one, indicating the presence
of reactive power and lower efficiency.
Capacitive Loads: Capacitive loads, such as capacitors,
store energy in an electric field and behave in the opposite way as inductive loads in
alternating current circuits. In a capacitive load, current leads voltage by 90 degrees (φ =
90°). This phase shift occurs because of the capacitor's ability to store and release charge,
causing the current to grow before the voltage reaches its peak. Capacitive loads, like
inductive loads, largely contribute to reactive power (Q) in the circuit; however, the reactive
power flows in the opposite way. The presence of capacitive loads can increase a circuit's

3. Page | 2
power factor by countering the effects of inductive loads, reducing overall reactive power
while enhancing efficiency.
RLC Circuits: RLC circuits, which are made up of
resistors (R), inductors (L), and capacitors (C), are important in the field of AC circuit
analysis. These circuits provide different behaviours and challenges depending on whether
they are arranged in series or parallel. Understanding resonance and the quality factor (Q-
factor), which are essential to the design and optimization of electronic circuits for a variety
of applications, is a vital component of their study.
Series RLC Circuits: A series RLC circuit consists of a
resistor, inductor, and capacitor all connected in series.
Figure1: Series RLC circuit example
The circuit's total impedance (Z) is a complex number that includes the resistive (R),
inductive (XL = jωL), and capacitive (XC = 1/jωC) reactances, where ω represents the angular
frequency of the AC supply. The impedance formula for a series RLC circuit is:
It shows that the inductive and capacitive reactances subtract since their effects are opposite.
In a series RLC circuit, resonance occurs when the
inductive and capacitive reactances have the same magnitude but opposite phase, leading
them to cancel out. At this time, the circuit's impedance is solely resistive, and its overall
impedance is at its lowest, resulting in maximum current flow.

4. Page | 3
Figure 2: Impedance in a series RLC circuit as a function of frequency
Figure 3: Series RLC circuit current as a function of frequency.
The resonant frequency (f0) can be measured with

5. Page | 4
Parallel RLC Circuits: Parallel RLC circuits have a
resistor, inductor, and capacitor linked in parallel, resulting in numerous routes for current
flow.
Figure 4: Parallel RLC circuit
The circuit's impedance is given by the following equation.
The resonance condition in parallel circuits is similar to
that in series circuits; it occurs when the net reactance is zero, enhancing the circuit's
resistance while limiting current flow. The resonant frequency is found using the same
formula as in series circuits.
Q-factor: The quality factor, or Q-factor, of an RLC circuit
is a dimensionless parameter that measures the sharpness of resonance. It is defined as the
resonant frequency divided by the bandwidth of the resonant peak, where the bandwidth is
the difference between frequencies at which the power is half of its peak value.

6. Page | 5
Figure 5: Series resonance circuit bandwidth
In series RLC circuits, the Q-factor is given by
And in parallel RLC circuits, it is given by.
A higher Q-factor suggests a smaller bandwidth and a
greater peak at resonance, implying reduced losses and a more selective circuit capable of
successfully filtering out a specific range of frequencies, i.e. acting as a band pass filter.
Steady-state Analysis:
Nodal Analysis: In AC circuits, nodal analysis involves
applying Kirchhoff's Current Law (KCL) to the nodes to determine their potentials in relation
to a reference/datum node. This approach employs the notion of node voltages as variables to
ease the process of solving circuits with many nodes. Nodal analysis in alternating current
circuits uses complex numbers to account for phase changes between voltage and current.

7. Page | 6
Impedances are employed instead of resistances, and the equations are written in the phasor
domain to solve for the unknown node voltages.
Mesh Analysis: Mesh analysis uses Kirchhoff's Voltage
Law (KVL) to analyze loops or meshes in a circuit. Mesh analysis in AC circuits, like nodal
analysis, takes into account impedances and phasor representations of voltage and current.
The goal is to create loop current equations for independent loops and solve them
concurrently to determine the phasor values associated with currents flowing around these
loops, which would substantially simplify the analysis of circuits that have multiple meshes.
Superposition Theorem: According to the superposition
theorem, in a linear circuit with multiple independent sources (voltage or current), the
response (voltage or current) in any branch is the algebraic sum of the responses caused by
each independent source acting alone, while all other independent sources are represented by
their internal impedances. This theorem is especially useful in AC circuits for determining the
influence of each frequency component or source inside the circuit.
Source Transformation: Source transformation is a
technique for simplifying circuit analysis that converts a voltage source in series with an
impedance to an equivalent current source in parallel with the same impedance, and vice
versa. This strategy is useful in situations when specific types of sources are easier to manage
or when attempting to reduce the number of sources in the circuit.
Figure 6: Source transformation
Thevenin and Norton Equivalent Circuits:
Thevenin's theorem: Thevenin's theorem states that a
linear two-terminal circuit may be substituted by an equivalent circuit made up of a voltage
source (Thevenin voltage) in series with an impedance.

8. Page | 7
Norton's theorem: Norton's theorem, on the other hand,
visualizes the circuit as a current source (Norton current) in parallel with an impedance.
These theorems are often used in AC circuit analysis to
help with the study of power systems and other complicated circuits.
Computer-based Tools for AC Circuit Analysis: With the
complexity of today's electrical systems, computer-based tools like SPICE, MATLAB, and
other circuit modeling software have become vital. These tools enable extensive modeling of
AC circuit behavior, including transient and steady-state analysis, by numerically solving
circuit equations. They allow complicated circuits to be modelled with several components
and sources, perform frequency response analysis, and anticipate circuit behavior under a
variety of operational situations without using physical prototypes.
REFERENCES:
1. https://www.monolithicpower.com/en/learning/mpscholar/ac-power/theory-and-
analysis/ac-circuit-analysis
2. Basic Electrical Engineering - Abhijit Chakrabarti , Sudipta Nath , Chandan Kumar
Chanda
3. Electrical and Electronic Technology – Edward Hughes
4. Network Analysis – ME Van Valkenburg
5. http://hyperphysics.phy-astr.gsu.edu/hbase/electric/serres.html
6. https://www.eeeguide.com/
7. https://en.wikipedia.org/
8. https://www.electrical4u.com/rlc-parallel-circuit/