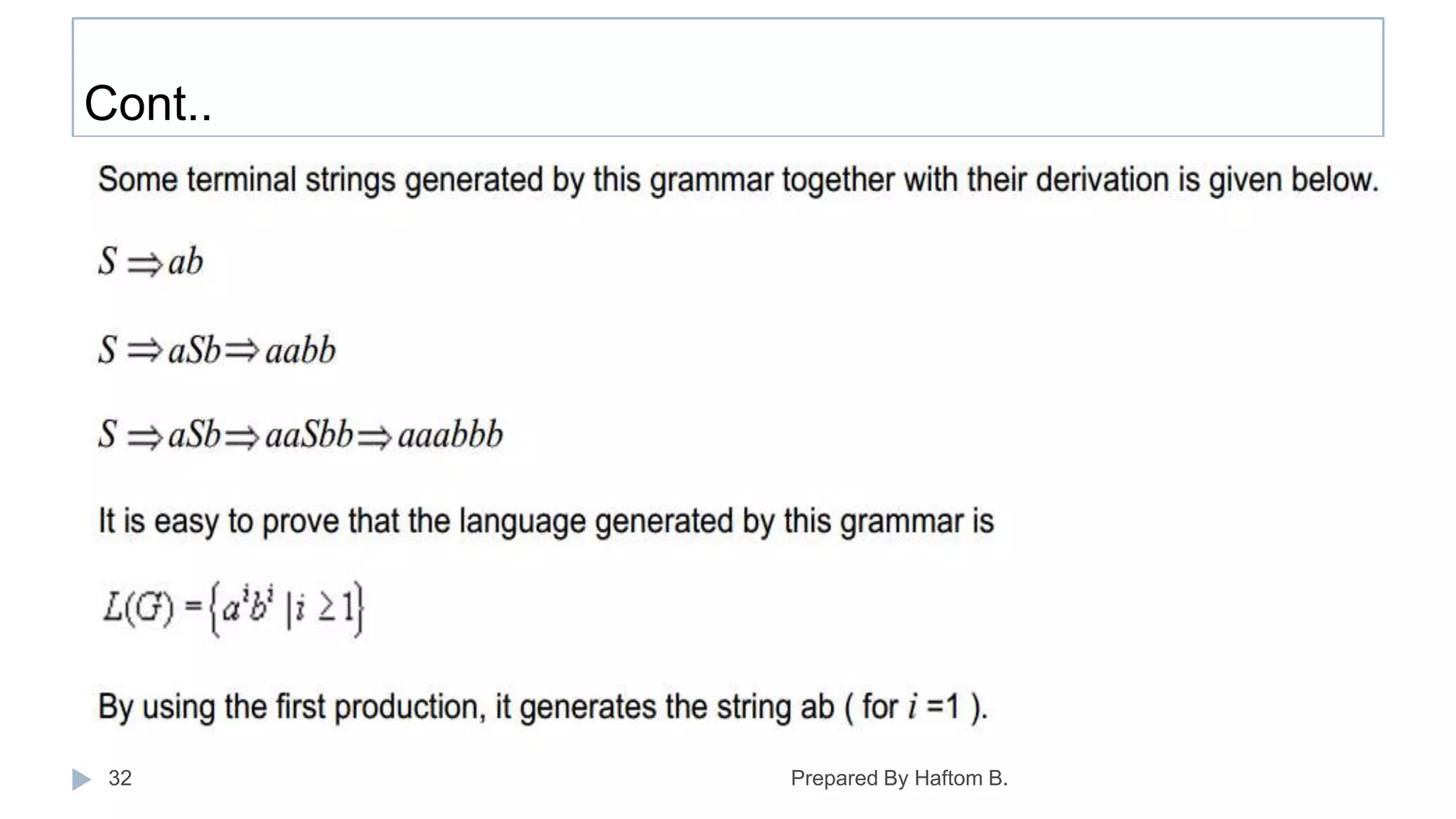
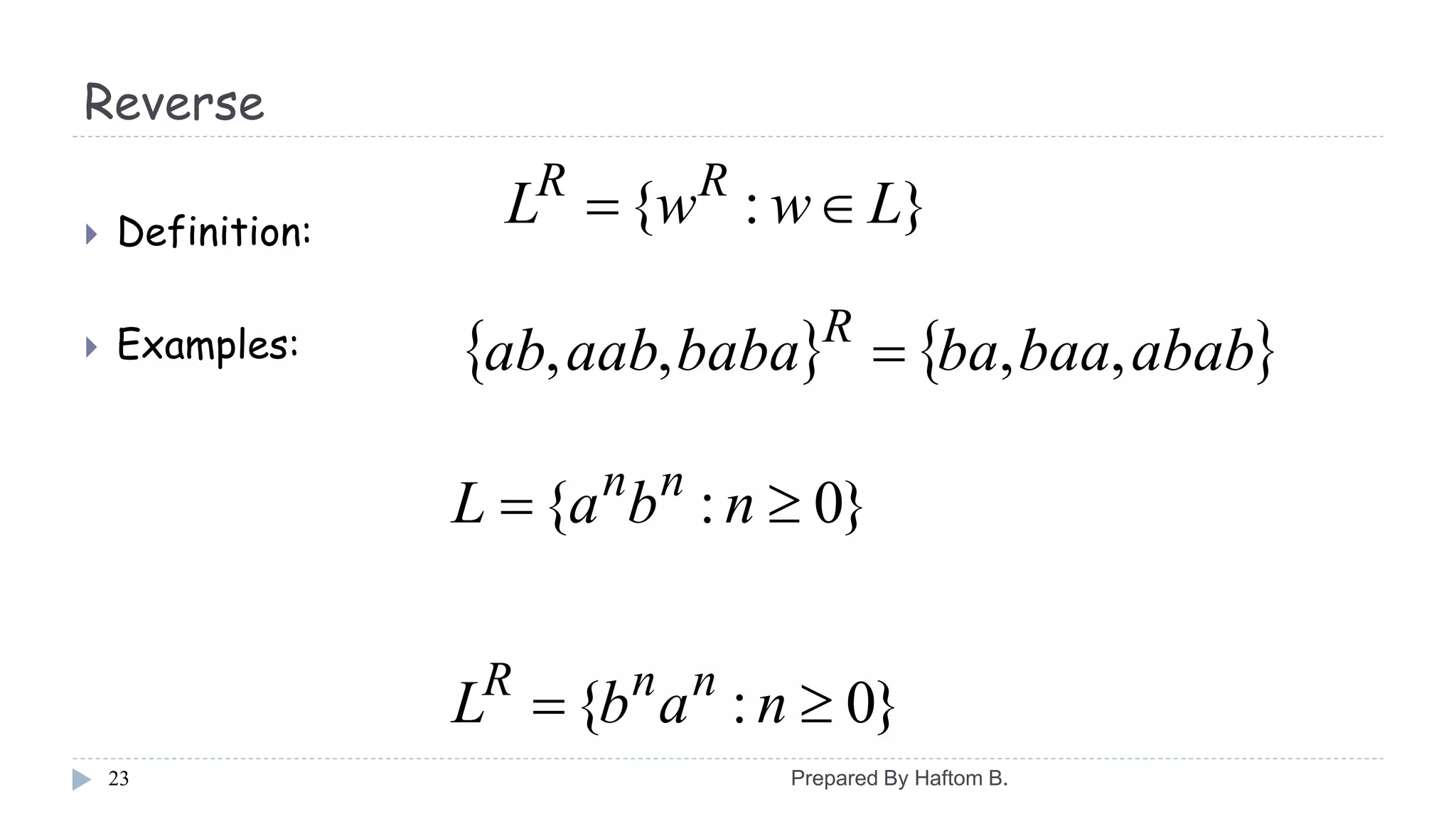This document provides information about strings, languages, and grammars. It defines alphabets as finite sets of symbols and strings as finite sequences of symbols from an alphabet. Operations on strings like concatenation and length are described. Languages are defined as sets of strings, and operations on languages like union and intersection are discussed. Grammars are introduced as a mechanism to describe languages using production rules. An example grammar is given and strings it can generate through derivations are shown.

1. Chapter One
Alphabets , Strings, Languages and
Grammars
Prepared By Haftom B.1

2. Prepared By Haftom B.2

3. Alphabets and Strings
A common way to talk about words, number, pairs of
words, etc. is by representing them as strings
To define strings, we start with an alphabet
Examples
An alphabet is a finite set of symbols.
S1 = {a, b, c, d, …, z}: the set of letters in English
S2 = {0, 1, …, 9}: the set of (base 10) digits
S3 = {a, b, …, z, #}: the set of letters plus the
special symbol #
S4 = {(, )}: the set of open and closed brackets
Prepared By Haftom B.3

4. Strings
The empty string will be denoted by E
Examples
A string over alphabet S is a finite sequence of symbols in S.
abfbz is a string over S1 = {a, b, c, d, …, z}
9021 is a string over S2 = {0, 1, …, 9}
ab#bc is a string over S3 = {a, b, …, z, #}
))()(() is a string over S4 = {(, )}
Prepared By Haftom B.4

5. Cont.…
We will use small alphabets:
Strings
5
abbaw
bbbaaav
abu



 ba,
baaabbbaaba
baba
abba
ab
a
Prepared By Haftom B.

6. String Operations
6
m
n
bbbv
aaaw


21
21


bbbaaa
abba
mn bbbaaawv  2121
1. Concatenation
abbabbbaaa
Prepared By Haftom B.

7. 7
12aaaw n
R

naaaw 21 ababaaabbb
2. Reverse
bbbaaababa
Prepared By Haftom B.

8. 3. String Length
Length:
Examples:
8
naaaw 21
nw 
1
2
4



a
aa
abba
Prepared By Haftom B.

9. Recursive Definition of Length
For any letter:
For any string :
Example:
9
1a
1 wwawa
4
1111
111
11
1





a
ab
abbabba
Prepared By Haftom B.

10. 4. Length of Concatenation
 Example:
10
vuuv 
853
8
5,
3,




vuuv
aababaabuv
vabaabv
uaabu
Prepared By Haftom B.

11. Proof of Concatenation Length
• Claim:
• Proof: By induction on the length
• Induction basis:
• From definition of length:
11
vuuv 
v
1v
vuuuv  1
Prepared By Haftom B.

12. Empty String
 A string with no letters:
 Observations:
12

abbaabbaabba
www





 0
Prepared By Haftom B.

13. Substring
Substring of string:
a subsequence of consecutive characters
String Substring
13
bbab
b
abba
ab
abbab
abbab
abbab
abbab
Prepared By Haftom B.

14. Prefix and Suffix
 Given string
 Prefixes Suffixes
14
abbab
abbab
abba
abb
ab
a


b
ab
bab
bbab
abbab uvw 
prefix
suffix
Prepared By Haftom B.

15. Another Operation
• Example:
• Definition:
•
15
 
n
n
wwww 
  abbaabbaabba 2
0
w
  0
abba
Prepared By Haftom B.

16. The * Operation
• : the set of all possible strings from alphabet
16
* 
 
 ,,,,,,,,,*
,
aabaaabbbaabaaba
ba


Prepared By Haftom B.

17. 17
The + Operation
: the set of all possible strings from
alphabet except



 
 ,,,,,,,,,*
,
aabaaabbbaabaaba
ba



*
 ,,,,,,,, aabaaabbbaabaaba

Prepared By Haftom B.

18. 1.2 Languages
 Languages can be used to describe problems with
“yes/no” answers, for example:
A language is a set of strings over an alphabet.
L1 = The set of all strings over S1 that contain
the substring “fool”
L2 = The set of all strings over S2 that are divisible by 7
= {7, 14, 21, …}
L3 = The set of all strings of the form s#s where s is any
string over {a, b, …, z}
L4 = The set of all strings over S4 where every ( can be
matched with a subsequent )
Prepared By Haftom B.18

19. Cont.…
 A language is any subset of
 Example 1:
 Languages:
19
*
 
 ,,,,,,,,*
,
aaabbbaabaaba
ba


 
 
},,,,,{
,,
aaaaaaabaababaabba
aabaaa


Prepared By Haftom B.

20. Example 2
 An infinite language
 is aabbaa ?
20
}0:{  nbaL nn
aaaaabbbbb
aabb
ab

L Labb
L
Prepared By Haftom B.

21. 21
Note that:
}{}{ 
0}{ 
1}{ 
0
Sets
Set size
Set size
String length
Prepared By Haftom B.

22. 1.2.1 Operations on Languages
• The usual set operations
• Complement:
22
   
   
     aaaaaabbbaaaaaba
ababbbaaaaaba
aaaabbabaabbbaaaaaba
,,,,
}{,,,
},,,{,,,





LL  *
   ,,,,,,, aaabbabaabbaa 
Prepared By Haftom B.

23. Reverse
 Definition:
 Examples:
23
}:{ LwwL RR

   ababbaabababaaabab R
,,,, 
}0:{
}0:{


nabL
nbaL
nnR
nn
Prepared By Haftom B.

24. Concatenation
 Definition:
 Example:
24
 2121 ,: LyLxxyLL 
  
 baaabababaaabbaaaab
aabbaaba
,,,,,
,,,

Prepared By Haftom B.

25. Another Operation
Definition:
Special case:
25
 
n
n
LLLL 
       bbbbbababbaaabbabaaabaaababababa ,,,,,,,,,,,
3

 
   



0
0
,, aaabbaa
L
Prepared By Haftom B.

26. More Examples
26
}0:{  nbaL nn
}0,:{2
 mnbabaL mmnn
2
Laabbaaabbb
Prepared By Haftom B.

27. Star-Closure (Kleene *)
• Definition:
• Example:
•
27
 210
* LLLL 
 















,,,,
,,,,
,,
,
*,
abbbbabbaaabbaaa
bbbbbbaabbaa
bba
bba

Prepared By Haftom B.

28. Positive Closure
 Definition:
28
 

*
21
L
LLL 
 











,,,,
,,,,
,,
,
abbbbabbaaabbaaa
bbbbbbaabbaa
bba
bba
Prepared By Haftom B.

29. Grammar
Prepared By Haftom B.29
A grammar is a mechanism used for describing
languages. This is one of the most simple but yet
powerful mechanism.
The grammar for English tells us what are the
words in it and the rules to construct sentences.

30. Formal definitions of a Grammar
Prepared By Haftom B.30
A grammar G is defined as a quadruple

31. Example
Prepared By Haftom B.31
Consider the grammar , where N = {S}, ={a, b} and P is
the set of the following production rules .
Some terminal strings are generated by this grammar together
with their derivation is given below

32. Cont..
Prepared By Haftom B.32

33. Cont.…
Prepared By Haftom B.33
 Example: Find a grammar for the language
It is possible to find a grammar for L by modifying the previous
grammar since we need to generate an extra b at the
end of the string .
We can do this by adding a production S Bb
where the non-terminal B generates