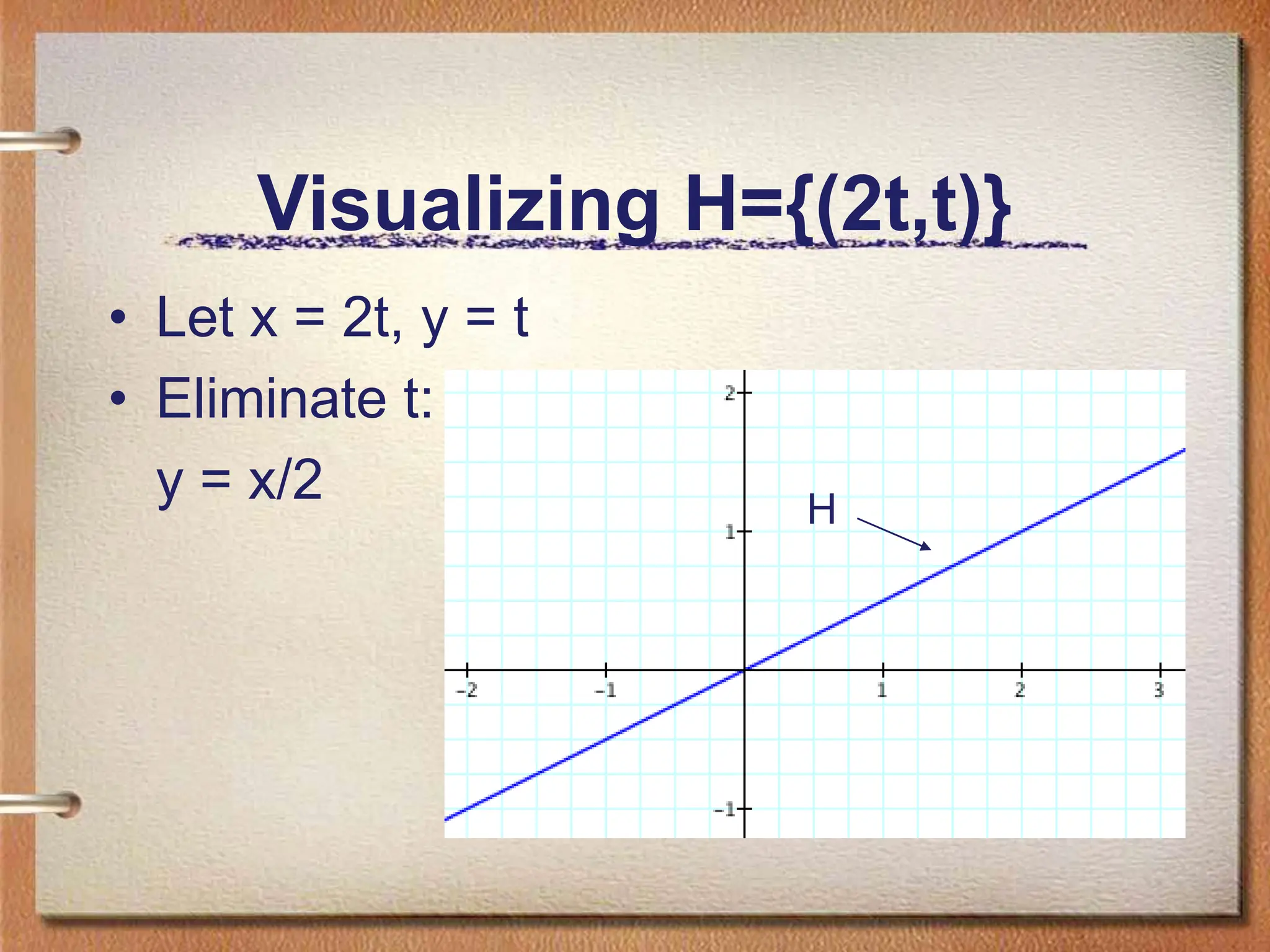
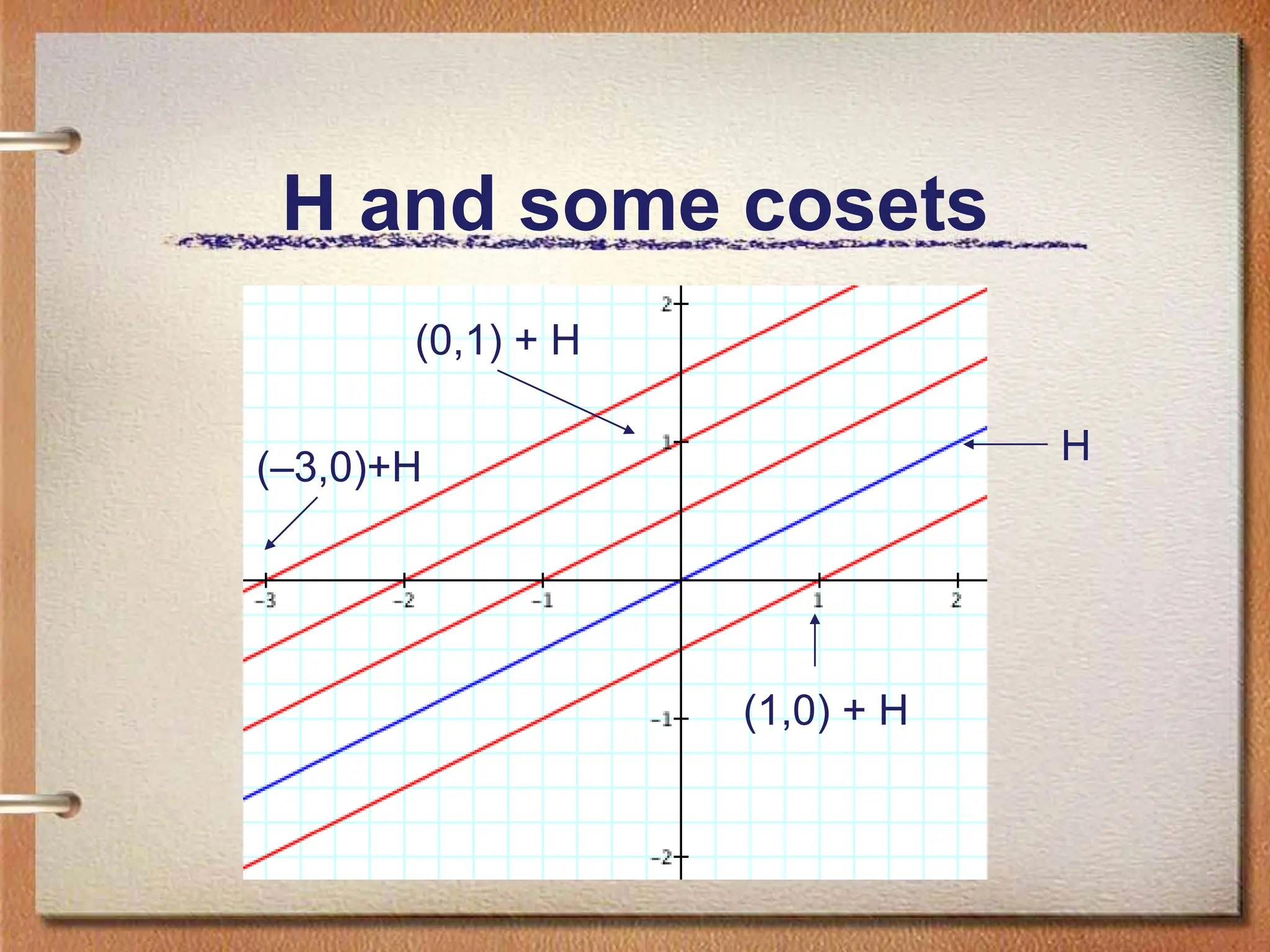
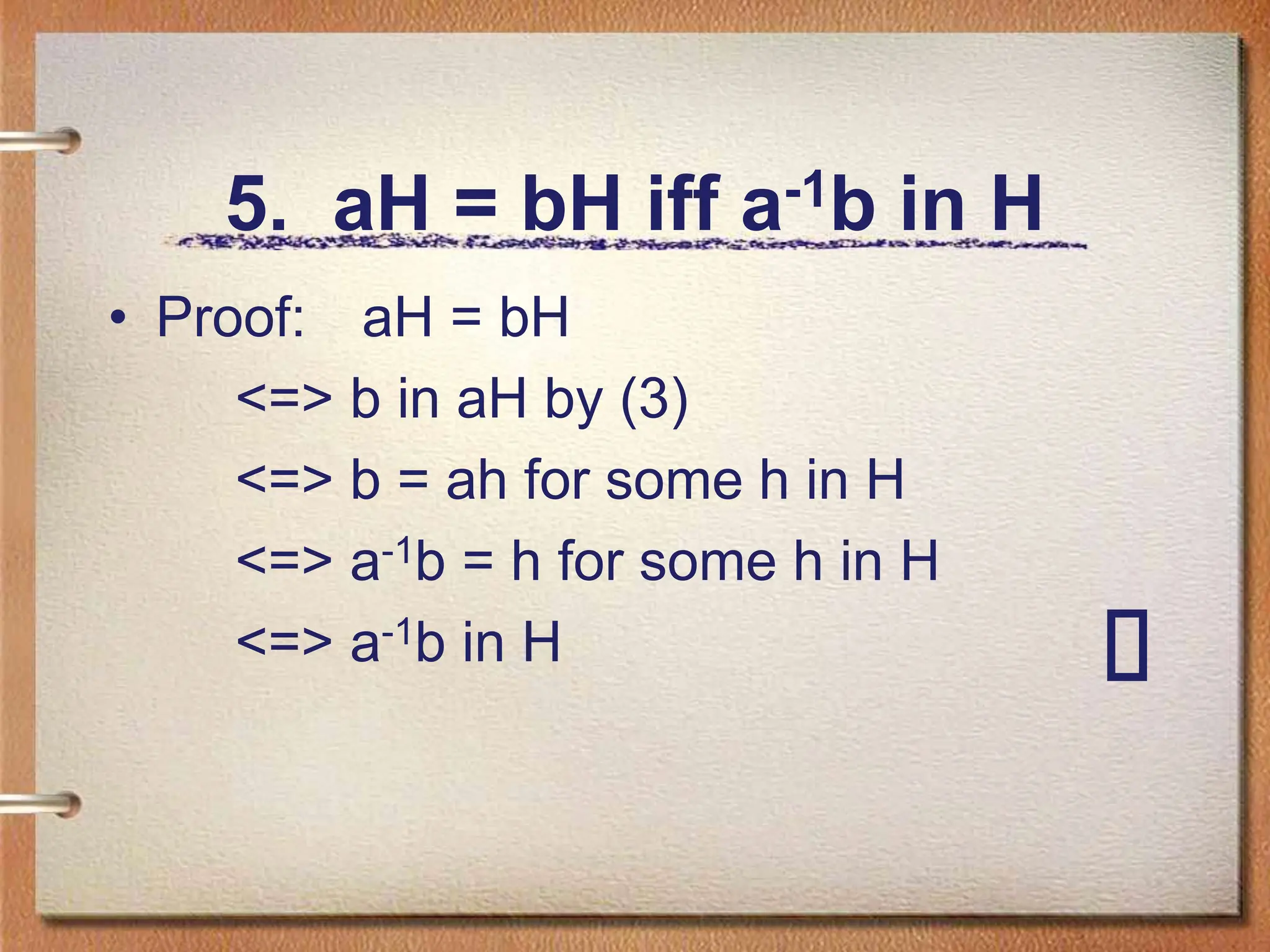
The document discusses Lagrange's theorem, a fundamental principle in group theory that relates to the size of symmetry groups and subgroup cosets. It explains the definitions and properties of left and right cosets, including examples and visualizations of these concepts in various groups. Furthermore, the document outlines criteria for coset relationships and implications regarding subgroup membership.

1. Cosets

2. Lagrange's Theorem
• The most important single theorem in
group theory. It helps answer:
– How large is the symmetry group of a
volleyball? A soccer ball?
– How many groups of order 2p where p is
prime? (4, 6, 10, 14, 22, 26, …)
– Is 2257-1 prime?
– Is computer security possible?
– etc.

3. Cosets
• Definition:
Let H ≤ G and a in G.
The left coset of H containing a is the set
aH = {ah | h in H}
The right coset of H containing a is the set
Ha = {ha | h in H}
• In additive groups use a+H and H+a.
• a is called the coset representative of aH.
• Similarly, aHa-1 ={aha-1 | h in H}

4. Cosets of K = {R0, V} in D4
• Some left cosets of K:
DK = {DR0, DV} = {D,R90}
R180K = {R180R0, R180V} = {R180, H}
• Some right cosets of K:
KD = {R0D, VD} = {D, R270}
KR180 = {R0R180,VR180} = {R180, H}

5. Cosets of K = {R0, V} in D4
• Left Cosets
R0K = {R0, V} = VK
R90K = {R90, D} = DK
R180K = {R180, H} = HK
R270K = {R270, D'}= D'K
• Right Cosets
KR0 = {R0, V} = KV
KR90 = {R90, D'} = KD'
KR180 = {R180, H} = KH
KR270 = {R270, D} = KD

6. More cosets
• Vectors under addition are a group:
(a,b) + (c,d) = (a+c,b+d)
Identity is (0,0)
Inverse of (a,b) is (-a,-b)
Associativity is easy to verify.
• H = {(2t,t) | t in R} is a subgroup.
Proof: (2a,a) - (2b,b) = (2(a-b),a-b)

7. Visualizing H={(2t,t)}
• Let x = 2t, y = t
• Eliminate t:
y = x/2 H

8. Cosets of H={(2t,t) | t in R}
• (a,b) + H = {(a+2t,b+t)}
Set x = a+2t, y = b+t and eliminate t:
y = b + (x-a)/2
The subgroup H is the line y = x/2.
The cosets are lines parallel to y = x/2 !

9. H and some cosets
H
(1,0) + H
(–3,0)+H
(0,1) + H

10. Left Cosets of <(123)> in A4
Let H = <(123)> {, (123), (132)}
H = {, (123), (132)}
(12)(34)H = {(12)(34), (243), (143)}
(13)(24)H = {(13)(24), (142), (234)}
(14)(23)H = {(14)(23), (134), (124)}

11. Properties of Cosets:
• Let H be a subgroup of G, and a,b in G.
• 1. a belongs to aH
• 2. aH = H iff a belongs to H
• 3. aH = bH iff a belongs to bH
• 4. aH and bH are either equal or disjoint
• 5. aH = bH iff a-1b belongs to H
• 6. |aH| = |bH|
• 7. aH = Ha iff H = aHa-1
• 8. aH ≤ G iff a belongs to H

12. 1. a belongs to aH
• Proof: a = ae belongs to aH.

13. 2. aH=H iff a in H
• Proof: (=>) Given aH = H.
By (1), a is in aH = H.
(<=) Given a belongs to H. Then
(i) aH is contained in H by closure.
(ii) Choose any h in H.
Note that a-1 is in H since a is.
Let b = a-1h. Note that b is in H. So
h = (aa-1)h = a(a-1h) = ab is in aH
It follows that H is contained in aH
By (i) and (ii), aH = H

14. 3. aH = bH iff a in bH
• Proof: (=>) Suppose aH = bH. Then
a = ae in aH = bH.
(<=) Suppose a is in bH. Then
a = bh for some h in H.
so aH = (bh)H = b(hH) = bH by (2).

15. 4. aH and bH are either
disjoint or equal.
• Proof: Suppose aH and bH are not
disjoint. Say x is in the intersection of
aH and bH.
Then aH = xH = bH by (3).
Consequently, aH and bH are either
disjoint or equal, as required.

16. 5. aH = bH iff a-1b in H
• Proof: aH = bH
<=> b in aH by (3)
<=> b = ah for some h in H
<=> a-1b = h for some h in H
<=> a-1b in H

17. 6. |aH| = |bH|
• Proof: Let ø: aH –>bH be given by
ø(ah) = bh for all h in H.
We claim ø is one to one and onto.
If ø(ah1) = ø(ah2), then bh1 = bh2
so h1 = h2. Therefore ah1 = ah2.
Hence ø is one-to-one.
ø is clearly onto.
It follows that |aH| = |bH| as required.

18. aH = Ha iff H = aHa-1
• Proof: aH = Ha
<=> each ah = h'a for some h' in H
<=> aha-1 = h' for some h' in H
<=> H = aHa-1.

19. aH≤G iff a in H
• Proof: (=>) Suppose aH ≤ G.
Then e in aH.
But e in eH, so eH and aH are not
disjoint. By (4), aH = eH = H.
(<=) Suppose a in H.
Then aH = H ≤ G.