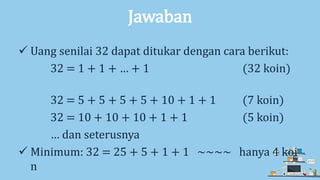
Dokumen tersebut membahas algoritma greedy. Algoritma greedy adalah metode yang populer untuk memecahkan masalah optimasi dengan mengambil pilihan terbaik pada setiap langkah tanpa mempertimbangkan konsekuensi di masa depan. Dokumen tersebut menjelaskan unsur-unsur algoritma greedy seperti himpunan kandidat, himpunan solusi, fungsi seleksi, dan fungsi kelayakan. Contoh masalah menukarkan uang 32 dengan koin dig

1. Ajeng Savitri P, M.Kom
Analysis & Strategy
of Algorithm
Pertemuan 8

2. OBJECTIVE
 To learn what Greedy Algorithm is
 To learn Greedy elements

3. Intro
 Persoalan optimasi (optimization problems)
merupakan persoalan yang menuntut pencarian solu
si optimum.
 Persoalan optimasi ada dua macam:
 Maksimasi (maximization)
 Minimasi (minimization)

4. Intro
• Solusi optimum (terbaik) adalah solusi yang bernilai
minimum atau maksimum dari sekumpulan alternati
f solusi yang mungkin.
• Elemen persoalan optimasi:
– kendala (constraints)
– fungsi objektif(atau fungsi optiamsi)

5. Solusi yang memenuhi semua kendala disebut
solusi layak (feasible solution).
Solusi layak yang mengoptimumkan fungsi optimasi
disebut solusi optimum.

6. Greedy
 Algoritma greedy merupakan metode yang paling
populer untuk memecahkan persoalan optimasi.
 Greedy = rakus, tamak, loba, ….
 Prinsip greedy adalah: “take what you can get now!”
 Algoritma greedy membentuk solusi langkah per
langkah (step by step).

7. Contoh Penggunaan Greedy
 Memilih beberapa jenis investasi (penanaman modal
)
 Mencari jalur tersingkat dari Bandung ke Surabaya
 Memilih jurusan di Perguruan Tinggi
 Bermain kartu remi

8. Terdapat banyak pilihan yang perlu dieksplorasi pa
da
setiap langkah solusi.
Oleh karena itu, pada setiap langkah harus dibuat
keputusan yang terbaik dalam menentukan pilihan.
Keputusan yang telah diambil pada suatu langkah ti
dak dapat diubah lagi pada langkah selanjutnya

9. Pendekatan yang digunakan di dalam algoritma gree
dy
adalah membuat pilihan yang “tampaknya”
memberikan perolehan terbaik, yaitu dengan memb
uat
pilihan optimum lokal (local optimum) pada setiap
langkah dengan harapan bahwa sisanya mengarah k
e
solusi optimum global (global optimum).

10.  Algoritma greedy adalah algoritma yang memecah
kan masalah langkah per langkah, pada setiap lan
gkah:
 mengambil pilihan yang terbaik yang dapat diperoleh p
ada
saat itu tanpa memperhatikan konsekuensi ke depan
(prinsip “take what you can get now!”)
 berharap bahwa dengan memilih optimum lokal pada se
tiap langkah akan berakhir dengan optimum global.

11. Elemen Algoritma Greedy
1. Himpunan kandidat
Berisi elemen-elemen pembentuk solusi.
2. Himpunan solusi
Berisi kandidat-kandidat yang terpilih sebagai solusi persoalan.
3. Fungsi seleksi (selection function)
Memilih kandidat yang paling memungkinkan mencapai solusi
optimal. Kandidat yang sudah dipilih pada suatu langkah tidak
pernah dipertimbangkan lagi pada langkah selanjutnya.

12. Elemen Algoritma Greedy (lanjutan)
4. Fungsi kelayakan (feasible)
Memeriksa apakah suatu kandidat yang telah dipilih dapat
memberikan solusi yang layak, yakni kandidat tersebut bersama-
sama dengan himpunan solusi yang sudah terbentuk tidak
melanggar kendala (constraints) yang ada. Kandidat yang layak
dimasukkan ke dalam himpunan solusi, sedangkan kandidat yang
tidak layak dibuang dan tidak pernah dipertimbangkan lagi.
5. Fungsi obyektif
Fungsi yang memaksimumkan atau meminimumkan nilai solusi
(misalnya panjang lintasan, keuntungan, dan lain-lain).

13. Contoh Masalah
 Persoalan:
Diberikan uang senilai 32. Tukar uang tersebut
dengan koin-koin uang 1, 5, 10, dan 25. Berapa jumla
h minimum koin yang diperlukan untuk penukaran
tersebut?

14. Jawaban
 Uang senilai 32 dapat ditukar dengan cara berikut:
32 = 1 + 1 + … + 1 (32 koin)
32 = 5 + 5 + 5 + 5 + 10 + 1 + 1 (7 koin)
32 = 10 + 10 + 10 + 1 + 1 (5 koin)
… dan seterusnya
 Minimum: 32 = 25 + 5 + 1 + 1 ~~~~ hanya 4 koi
n

15. Penjelasan
 Strategi greedy yang digunakan adalah:
Pada setiap langkah, pilihlah koin dengan nilai sebesar mungkin
dari himpunan koin yang tersisa dengan syarat (kendala) tidak
melebihi nilai uang yang ditukarkan.
 Tinjau masalah menukarkan uang 32 penyelesaian :
Langkah 1: pilih 1 buah koin 25 (Total = 25)
Langkah 2: pilih 1 buah koin 5 (Total = 25 + 5 = 30)
Langkah 3: pilih 2 buah koin 1 (Total = 25+5+1+1= 32)
 Solusi: Jumlah koin minimum = 4 (solusi optimal!)

16. Penjelasan dengan Menggunakan Greedy
 Himpunan kandidat:
Himpunan koin yang merepresentasikan nilai 1, 5, 10, 25, pali
ng sedikit mengandung satu koin untuk setiap nilai.
 Himpunan solusi:
Total nilai koin yang dipilih tepat sama jumlahnya dengan
nilai uang yang ditukarkan (32).
 Fungsi seleksi:
Pilihlah koin yang bernilai tertinggi dari himpunan kandidat
yang tersisa.

17. Penjelasan dengan Menggunakan Greedy
 Fungsi layak:
memeriksa apakah nilai total dari himpunan koin yang
dipilih tidak melebihi jumlah uang yang harus dibayar.
 Fungsi obyektif
jumlah koin yang digunakan minimum.

18. REFFERENCE
 Munir, Rinaldi. Diktat Kuliah “Kompleksitas Algoritma”, Departemen T
eknik Informatika ITB
 Levitin, Anany. 2012. Introduction to the Design and Analysis of A
lgorithms, 3rd Edition.Addison Wesley

19. Terima Kasih
ajeng.savitri@teknokrat.ac.id
https://teknokrat.ac.id/en/
https://spada.teknokrat.ac.id/