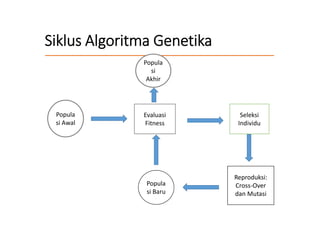
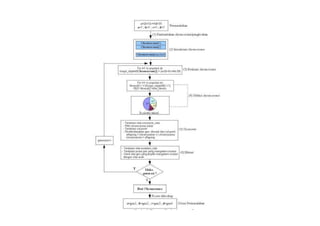
Algoritma genetika pertama kali diperkenalkan oleh John Holland pada tahun 1975. Algoritma genetika didasarkan pada mekanisme evolusi biologi seperti seleksi alam, crossover, dan mutasi untuk menyelesaikan masalah optimisasi. Algoritma genetika menggunakan populasi kromosom yang berevolusi melalui operasi genetika untuk menemukan solusi optimal dari suatu masalah.

1. ALGORITMA
GENETIKA
Oleh : Ali Mulyanto, M.Kom

2. Pendahuluan
• Algoritma genetika pertama kali diperkenalkan oleh
John Holland dari Universitas Michigan (1975),
Kemudian dikembangkan oleh David Goldberg
• Algoritma Genetika adalah algoritma pencarian
heuristic yang didasarkan atas mekanisme evolusi
biologis.
• Algoritma Genetika juga merupakan metode
pencarian yang disesuaikan dengan prosess
generika dari orginisme biologi yang berdasar pada
teori evolusi Charles Darwin

3. Pendahuluan cont’s
• Algoritma Genetika terinspirasi dari mekanisme
seleksi alam, dimana individu yang lebih kuat
kemungkinan akan menjadi pemenang dalam
lingkungan yang kompetitif dan solusi yang optimal
dapat diperoleh dan diwakilkan oleh pemenang
akhir dari permainan genetika
• Pada Algoritma Genetika tersedia solusi yang
diterapkan pada sebuah populasi individu yang
masing-masing mewakili solusi yang mungkin.
Setiap solusi yang mungkin disebut dengan
kromosom.

4. Pendahuluan cont’s
• Kumpulan chromosome-chromosome tersebut
disebut sebagai populasi.
• Sebuah chromosome dibentuk dari komponen-
komponen penyusun yang disebut sebagai gen dan
nilainya dapat berupa bilangan numerik, biner,
simbol ataupun karakter tergantung dari
permasalahan yang ingin diselesaikan.
• Chromosome-chromosome tersebut akan
berevolusi secara berkelanjutan yang disebut
dengan generasi

5. Pendahuluan cont’s
• Untuk memilih chromosome yang tetap
dipertahankan untuk generasi selanjutnya
dilakukan proses yang disebut dengan seleksi.
• Proses seleksi chromosome menggunakan konsep
aturan evolusi Darwin yang telah disebutkan
sebelumnya yaitu chromosome yang mempunyai
nilai fitness tinggi akan memiliki peluang lebih
besar untuk terpilih lagi pada generasi selanjutnya.

6. Individu dalam Algoritma Genetika

7. Struktur Umum
• Populasi, istilah pada teknik pencarian yang
dilakukan sekaligus atas sejumlah solusi yang
mungkin
• Kromosom, individu yang terdapat dalam satu
populasi dan merupakan suatu solusi yang
masih berbentuk simbol.
• Generasi, populasi awal dibangun secara acak
sedangkan populasi selanjutnya merupakan hasil
evolusi kromosom-kromosom melalui iterasi

8. Struktur Umum cont’s
• Fungsi Fitness, alat ukur yang digunakan untuk
proses evaluasi kromosom. Nilai fitness dari suatu
kromosom akan menunjukkan kualitas kromosom
dalam populasi tersebut.
• Generasi berikutnya dikenal dengan anak
(offspring) terbentuk dari gabungan 2 kromosom
generasi sekarang yang bertindak sebagai induk
(parent) dengan menggunakan operator penyilang
(crossover).
• Mutasi, operator untuk memodifikasi kromosom.

9. Popula
si Awal
Evaluasi
Fitness
Seleksi
Individu
Reproduksi:
Cross-Over
dan Mutasi
Popula
si Baru
Siklus Algoritma Genetika
Popula
si
Akhir

10. Komponen Utama
Ada 6 komponen utama algoritma genetika :
1. Teknik Penyandian
• Teknik penyandian meliputi penyandian gen dari
kromosom
• Gen merupakan bagian dari kromosom, satu gen
biasanya akan mewakili satu variabel
• Gen dapat direpresentasikan dalam bentuk :
string bit, pohon, array bilangan real, daftar
aturan, elemen permutasi, elemen program dan
lainlain

11. Komponen Utama cont’s
• Kromosom dapat direpresentasikan dengan
menggunakan :
• String bit : 10011, 11101
• Bilangan Real : 65.65, 562.88
• Elemen Permutasi : E2, E10
• Daftar Aturan : R1, R2, R3
• Elemen Program : pemrograman genetika
• Struktur lainnya

12. Komponen Utama cont’s
2. Inisialisasi
• Setelah ukuran populasi ditentukan, kemudian harus
dilakukan inisialisasi terhadap kromosom yang terdapat
pada populasi tersebut
• Inisialisasi kromosom dilakukan secara acak, namun
demikian harus tetap memper-hatikan domain solusi
dan kendala permasalahan yang ada
3. Fungsi Evaluasi
Ada 2 hal yang harus di-lakukan dalam melakukan
evaluasi kromosom yaitu : evaluasi fungsi objektif dan
konversi fungsi objektif ke dalam fungsi fitness

13. Komponen Utama cont’s
4. Seleksi
• Bertujuan untuk memberikan kesempatan reproduksi
yang lebih besar bagi anggota populasi yang paling fit
 Ada beberapa metode seleksi dari induk, antara lain :
• Rank-based fitness assigment
• Roulette wheel selection
• Stochastic universal sampling
• Local selection
• Truncation selection
• Tournament selection

14. Komponen Utama cont’s
5. Operator Genetika / crossover
• Crossover adalah fase paling signifikan dalam
algoritma genetika. Untuk setiap pasangan orang tua
yang akan dikawinkan, titik crossover dipilih secara
acak dari dalam gen.
• Macam-macam crosover
a. Crossover satu titik
b. Crossover banyak titik
c. Crossover seragam
d. Crossover dengan permutasi

15. Contoh crossover
New

16. Komponen Utama cont’s
• Mutasi
Pada keturunan baru tertentu yang terbentuk,
beberapa gen mereka dapat mengalami mutasi
dengan probabilitas acak yang rendah. Ini
menyiratkan bahwa beberapa bit dalam string bit
dapat dibalik.

17. Komponen Utama cont’s
6. Penetuan Parameter
• Parameter adalah parameter kontrol algoritma
genetika, yaitu : ukuran populasi (popsize),
peluang crossover (pc) dan peluang mutasi
(pm).
• Ukuran populasi sebaiknya tidak lebih kecil
dari 30, untuk sembarang jenis permasalahan

18. Algoritma Genetika
1. Pembentukan chromosome(menentukan variable untuk
gen-gen pembentuk chromosome)
2. Inisialisasi (memberikan nilai awal gen-gen dengan nilai
acak sesuai batasan yang telah ditentukan)
3. Evaluasi Chromosome (menggunakan fungi objektif)
4. Seleksi Chromosome (memilih chromosome yang
mempunyai fungsi_objektif kecil mempunyai
kemungkinan terpilih yang besar atau mempunyai nilai
probabilitas yang tinggi).
5. Crossover (memilih secara acak satu posisi dalam
chromosome induk kemudian saling menukar gen)
6. Mutasi (Proses mutasi dilakukan dengan cara mengganti
satu gen yang terpilih secara acak dengan suatu nilai baru
yang didapat secara acak)
7. Jika solusi belum optimal kembali ke langkah ke-3

19. Contoh Kasus

20. contoh
• Misalkan ada persamaan
a+2b+3c+4d = 30
kita mencari nilai a, b, c, dan d yang memenuhi
persamaan diatas. Kita mencoba menggunakan
algoritma genetika untuk menyelesaikan
permasalahan diatas.

21. Langkah-langkah Penyelesaian
1. Pembentukan chromosome
2. Inisialisasi
3. Evaluasi Chromosome
4. Seleksi Chromosome
5. Crossover
6. Mutasi

23. 1. Pembentukan chromosome
• Karena yang dicari adalah nilai a, b, c, d maka
variabel a, b, c, d dijadikan sebagai gen-gen
pembentuk chromosome.
• Batasan nilai variabel a adalah bilangan integer 0
sampai 30. Sedangkan batasan nilai variabel b,
c,dan d bilangan integer 0 sampai 10.

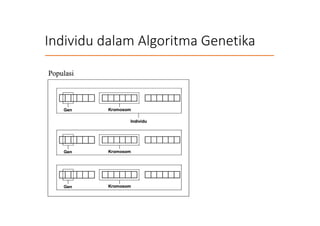
24. 2. Inisialisasi
Proses inisialisasi dilakukan dengan cara memberikan
nilai awal gen-gen dengan nilai acak sesuai batasan yang
telah ditentukan. Misalkan kita tentukan jumlah
Cromosome adalah 6, maka:
• Chromosome[1] = [a;b;c;d] = [12;05;03;07]
• Chromosome[2] = [a;b;c;d] = [02;01;08;03]
• Chromosome[3] = [a;b;c;d] = [10;04;03;04]
• Chromosome[4] = [a;b;c;d] = [20;01;10;06]
• Chromosome[5] = [a;b;c;d] = [01;04;03;07]
• Chromosome[6] = [a;b;c;d] = [20;05;07;01]

25. 3. Evaluasi Chromosome
• Untuk mengevaluasi chromosome menggunakan
fungsi_objektif yang dapat digunakan untuk
mendapatkan solusi adalah
fungsi_objektif(chromosome) =
| (a+2b+3c+4d) – 30 |
• Kita hitung fungsi_objektif dari chromosome yang
telah dibangkitkan:

26. 3. Evaluasi Chromosome cont’s
• f(chromosome[1]) = Abs(( 12 + 2*5 + 3*3 + 4*7 ) – 30) =29
• f (chromosome[2]) = Abs(( 2 + 2*1 + 3*8 + 4*3 ) – 30) = 10
• f (chromosome[3]) = Abs(( 10 + 2*4 + 3*3 + 4*4 ) – 30) =13
• f (chromosome[4]) = Abs(( 20 + 2*1 + 3*10 + 4*6 ) – 30) = 46
• f (chromosome[5]) = Abs(( 1 + 2*4 + 3*3 + 4*7 ) – 30) = 16
• f (chromosome[6]) = Abs(( 20 + 2*5 + 3*7 + 4*1 ) – 30) = 25
Rata-rata dari fungsi objektif adalah:
(29+10+13+46+16+25)/6 = 23,16

27. 4. seleksi Chromosome
• Proses seleksi dilakukan dengan cara memilih
chromosome yang mempunyai fungsi_objektif kecil
(mempunyai kemungkinan terpilih yang besar atau
mempunyai nilai probabilitas yang tinggi).
• Untuk itu dapat digunakan fungsi fitness =
(1/(1+fungsi_objektif)), fungsi_objektif perlu
ditambah 1 untuk menghindari kesalahan program
yang diakibatkan pembagian oleh 0.

28. 4. seleksi Chromosome cont’s
fitness[1] = 1 / (fungsi_objektif[1]+1) = 1 / 30 = 0.0333
fitness[2] = 1 / (fungsi_objektif[2]+1) = 1 / 11 = 0.0909
fitness[3] = 1 / (fungsi_objektif[3]+1) = 1 / 14 = 0.0714
fitness[4] = 1 / (fungsi_objektif[4]+1) = 1 / 47 = 0.0212
fitness[5] = 1 / (fungsi_objektif[5]+1) = 1 / 17 = 0.0588
fitness[6] = 1 / (fungsi_objektif[6]+1) = 1 / 26 = 0.0385
total_fitness = 0.0333 + 0.0909 + 0.0714 + 0.0212
+ 0.0588 + 0.0385 = 0.3141

29. 4. seleksi Chromosome cont’s
Rumus untuk mencari probabilitas:
P[i] = fitness[i] / total_fitness
P[1] = 0.0333 / 0.3141 = 0.1060
P[2] = 0.0909 / 0.3141 = 0.2894
P[3] = 0.0714 / 0.3141 = 0.2273
P[4] = 0.0212 / 0.3141 = 0.0675
P[5] = 0.0588 / 0.3141 = 0.1872
P[6] = 0.0385 / 0.3141 = 0.1226

30. 4. seleksi Chromosome cont’s
• Untuk proses seleksi kita gunakan roulete wheel
(Prosesnya adalah dengan membangkitkan bilangan
acak R dalam range 0-1)
• untuk itu kita harus mencari dahulu nilai kumulatif
probabilitasnya (pc):
C[1] = 0.1060
C[2] = 0.1060 + 0.2894 = 0.3954
C[3] = 0.1060 + 0.2894 + 0.2273 = 0.6227
C[4] = 0.1060 + 0.2894 + 0.2273 + 0.0675 = 0,6902
C[5] = 0.1060 + 0.2894 + 0.2273 + 0.0675 + 0.1872 = 0,8774
C[6] = 0.1060 + 0.2894 + 0.2273 + 0.0675 + 0.1872 + 0.1226 = 1

31. 4. seleksi Chromosome cont’s
• Setelah dihitung cumulative probabilitasnya maka
proses seleksi menggunakan roulete-wheel dapat
dilakukan. Prosesnya adalah dengan
membangkitkan bilangan acak R dalam range 0-1.
• Jika R[k] < C[1] maka pilih chromosome 1 sebagai
induk, selain itu pilih chromosome ke-k sebagai
induk dengan syarat C[k-1] < R < C[k]. Kita putar
roulete wheel sebanyak jumlah populasi yaitu 6 kali
(bangkitkan bilangan acak R) dan pada tiap putaran,
kita pilih satu chromosome untuk populasi baru.

32. 4. seleksi Chromosome cont’s
• Misal bilangan acak yg dipilih pada setiap putaran
sbb:
R[1] = 0.201
R[2] = 0.284
R[3] = 0.009
R[4] = 0.822
R[5] = 0.390
R[6] = 0.501
• Angka acak pertama R[1], Karena C[1] < R[1] < C[2],
maka pilih chromosome[2] sebagai chromosome
pada populasi baru.

33. 4. seleksi Chromosome cont’s
K Bil. Acak (R) Probability
Cumulative (PC)
Jika R < PC[k], pilih C[1], jika PC[k-1] <
R < PC[k], pilih C[k]
1 R[1] = 0.201 0.0333 C2
2 R[2] = 0.284 0.3954 C2
3 R[3] = 0.009 0.6227 C1
4 R[4] = 0.822 0.6902 C5
5 R[5] = 0.390 0.8774 C2
6 R[6] = 0.501 1 C3

34. 4. seleksi Chromosome cont’s
Dari bilangan acak yang telah dibangkitkan diatas maka populasi
chromosome hasil proses seleksi adalah:
chromosome[1] = chromosome[2]
chromosome[2] = chromosome[2]
chromosome[3] = chromosome[1]
chromosome[4] = chromosome[5]
chromosome[5] = chromosome[2]
chromosome[6] = chromosome[3]
Chromosome baru hasil proses seleksi:
chromosome[1] = [02;01;08;03]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;07]
chromosome[4] = [01;04;03;07]
chromosome[5] = [02;01;08;03]
chromosome[6] = [10;04;03;04]

35. 5. Crossover
• Metode yang digunakan salah satunya adalah one-
cut point, yaitu memilih secara acak satu posisi
dalam chromosome induk kemudian saling
menukar gen.
• Chromosome yang dijadikan induk dipilih secara
acak dan jumlah chromosome yang mengalami
crossover dipengaruhi oleh parameter
crossover_rate (ρc).

36. 5. Crossover cont’s
Misal kita tentukan crossover probability adalah sebesar 25%
atau 0.25, maka diharapkan dalam satu generasi ada 50%
Chromosome (3 chromosome) dari satu generasi yang
mengalami proses crossover.
Prosesnya adalah sebagai berikut:
a. kita bangkitkan bilangan acak R sebanyak jumlah populasi
R[1] = 0.191
R[2] = 0.259
R[3] = 0.760
R[4] = 0.006
R[5] = 0.159
R[6] = 0.340
Misal pc = 0.25
Jika R[k] < ρc, maka yang dijadikan induk adalah
chromosome[1], chromosome[4] dan chromosome[5].

37. 5. Crossover cont’s
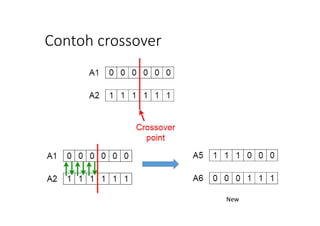
b. menentukan posisi crossover.
Ini dilakukan dengan cara membangkitkan bilangan
acak dengan batasan 1 sampai (panjang
chromosome-1), dalam kasus ini bilangan acak yang
dibangkitkan adalah 1 – 3. Misalkan didapatkan
posisi crossover adalah 1 maka chromosome induk
akan dipotong mulai gen ke 1 kemudian potongan
gen tersebut saling ditukarkan antar induk.
chromosome[1] >< chromosome[4]
chromosome[4] >< chromosome[5]
chromosome[5] >< chromosome[1]

38. 5. Crossover cont’s
c. Posisi cut-point crossover dipilih menggunakan
bilangan acak 1-3 sebanyak jumlah crossover yang
terjadi, misal
C[1] = 1
C[2] = 1
C[3] = 2

39. 5. Crossover cont’s
offspring[1] = chromosome[1] >< chromosome[4]
= [02;01;08;03] >< [01;04;03;07]
= [02;04;03;07]
offspring[4] = Chromosome[4] >< Chromosome[5]
= [01;04;03;07] >< [02;01;08;03]
= [01;01;08;03]
offspring[5] = Chromosome[5] >< Chromosome[1]
= [02;01;08;03] >< [02;01;08;03]
= [02;01;08;03]

40. 5. Crossover cont’s
Dengan demikian populasi Chromosome setelah
mengalami proses crossover menjadi:
chromosome[1] = [02;04;03;07]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;07]
chromosome[4] = [01;01;08;03]
chromosome[5] = [02;01;08;03]
chromosome[6] = [10;04;03;04]

41. 6. Mutasi
• Jumlah chromosome yang mengalami mutasi dalam
satu populasi ditentukan oleh parameter
mutation_rate.
• Proses mutasi dilakukan dengan cara mengganti satu
gen yang terpilih secara acak dengan suatu nilai baru
yang didapat secara acak.
• Prosesnya adalah sebagai berikut. Pertama kita hitung
dahulu panjang total gen yang ada dalam satu populasi.
• Dalam kasus ini panjang total gen adalah
total_gen= (jml gen dalam chromosome) *jml populasi
= 4 * 6
= 24

42. 6. Mutasi cont’s
• Untuk memilih posisi gen yang mengalami mutasi
dilakukan dengan cara membangkitkan bilangan
integer acak antara 1 sampai total_gen, yaitu 1
sampai 24.
• Jika bilangan acak yang kita bangkitkan lebih kecil
daripada variabel mutation_rate (ρm) maka pilih
posisi tersebut sebagai sub-chromosome yang
mengalami mutasi.
• Misal ρm kita tentukan 10% maka diharapkan ada
10% dari total_gen yang mengalami populasi:
jumlah mutasi = 0.1 * 24 = 2.4 = 2

43. 6. Mutasi cont’s
• Misalkan setelah kita bangkitkan bilangan acak
terpilih posisi gen 12 dan 18 yang mengalami
mutasi.
• Dengan demikian yang akan mengalami mutasi
adalah chromosome ke-3 gen nomor 4 dan
Chromosome ke-5 gen nomor 2.
• Maka nilai gen pada posisi tersebut kita ganti
dengan bilangan acak 0-30.

44. 6. Mutasi cont’s
Misalkan bilangan acak yang terbangkitkan adalah 2
dan 5. Maka populasi chromosome setelah
mengalami proses mutasi adalah:
chromosome[1] = [02;04;03;07]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;02]
chromosome[4] = [01;01;08;03]
chromosome[5] = [02;05;08;03]
chromosome[6] = [10;04;03;04]

45. Setelah proses mutasi maka
kita telah menyelesaikan satu
iterasi dalam algoritma
genetika atau disebut dengan
satu generasi.

46. Chromose Baru
Nilai Gen Pada Chromosome setelah satu generasi
adalah:
chromosome[1] = [02;04;03;07]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;02]
chromosome[4] = [01;01;08;03]
chromosome[5] = [02;05;08;03]
chromosome[6] = [10;04;03;04]

47. Hitung Fungsi Objektif
fungsi_objective setelah satu generasi adalah:
• fungsi_objektif[1] = Abs(( 2 + 2*4 + 3*3 + 4*7 ) – 30) = 17
• fungsi_objektif[2] = Abs(( 2 + 2*1 + 3*8 + 4*3 ) – 30) = 10
• fungsi_objektif[3] = Abs(( 12 + 2*5 + 3*3 + 4*2 ) – 30) =9
• fungsi_objektif[4] = Abs(( 1 + 2*1 + 3*8 + 4*3 ) – 30)=9
• fungsi_objektif[5] = Abs(( 2 + 2*5 + 3*8 + 4*3 ) – 30) = 18
• fungsi_objektif[6] = Abs(( 10 + 2*4 + 3*3 + 4*4 ) – 30) =13
Rata-rata fungsi objektif setelah satu generasi adalah:
( 17 + 10 + 9 + 9 + 18 + 13) / 6 = 76 / 6 = 12.67

48. Kesimpulan
• Dapat dilihat dari hasil perhitungan fungsi objektif
diatas bahwa setelah satu generasi, nilai hasil rata-
rata fungsi_objektif lebih menurun dibandingkan
hasil fungsi_objektif pada saat sebelum mengalami
seleksi, crossover dan mutasi. Hal ini menunjukkan
bahwa chromosome atau solusi yang dihasilkan
setelah satu generasi lebih baik dibandingkan
generasi sebelumnya.

49. Kasus Ke-2
Algoritma Genetika untuk mecari kata secara Acak

50. Contoh
• Sebuah Kata ditentukan sebagai target, misalnya :
BASUKI. Bila huruf diberi nilai dengan nilai huruf
alfabet, maka targetnya bisa dinyatakan dengan
besaran numerik, sbb :
TARGET = [2 1 19 21 11 9]
• Komputer akan membangkitkan kata dengan
jumlah huruf yang sama dengan target secara acak
secara terus menerus hingga diperoleh kata yang
sama dengan target.

51. • Individu adalah satu kata yang muncul dari proses
acak, misalnya: AGHSQE atau [1 7 8 19 17 5]
• Satu individu mempunyai n gen integer yang setiap
gennya menyatakan no urut alfabet
• Nilai fitness adalah inversi dari perbedaan antara
nilai kata yang muncul (individu) dan target yang
ditentukan. Misal kata yang muncul adalah AGHSQE
dan terget yang ditentukan adalah BASUKI maka,
nilai perbedaannya adalah

52. Nilai fitness dideifiniskan sbb
Dimana gn adalah gen ke n dari individu ke k dan gen ke k dari target

53. • Polupasi awal dibangkitkan dengan cara
membangkitkan semua huruf dalam sejumlah kata
(individu) yang dibangkitkan

54. • Seleski menggunakan roullete wheel
• Cros over

55. • Mutasi dengan mengacak nilai 1-26

56. Hasil Algoritma Genetika

57. Soal Kasus
Lakakun pencarian kata sesuai nama masing-masing
menggunakan algoritma genetika, spasi bernilai nol