Downloaded 114 times
Uploaded byMahfuzul Yamin
AI-MiniMax Algorithm and Alpha Beta Reduction
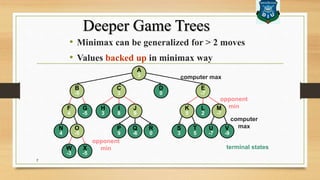
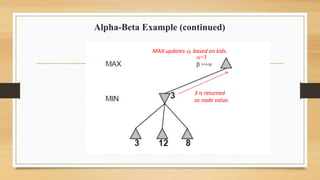
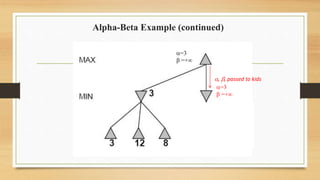
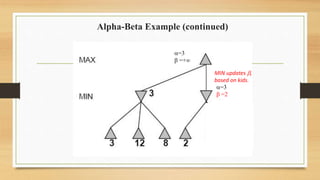
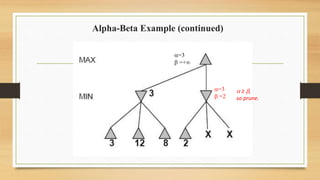
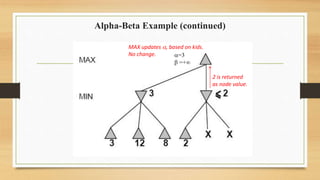
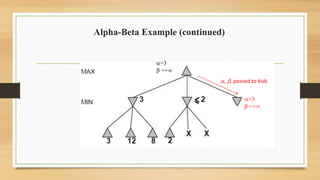
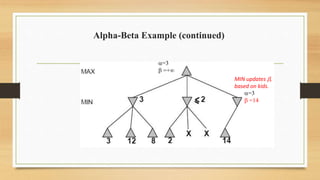
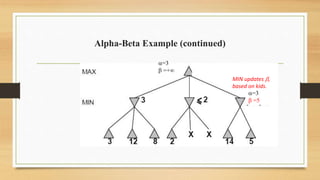
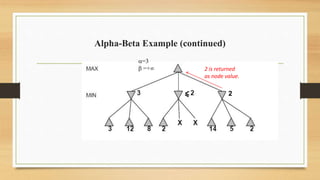
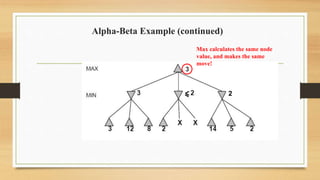
The document discusses minimax decision-making in game theory, focusing on its properties, requirements, and algorithmic implementation. It also covers alpha-beta pruning, which enhances the efficiency of minimax by eliminating unnecessary subtree evaluations, thus preserving optimality. An example is provided to illustrate the application of alpha-beta pruning in decision-making.
AI-MiniMax Algorithm and Alpha Beta Reduction
- 1. Minimax and Alpha-BetaReduction
- 2. Group Members Md. MusabbirHussain 141-15-3077 Faiaz Ahamed Raihan 141-15-3260 Md. Mahfuzul Yamin 141-15-3429 Ms. Habiba Sultana 141-15-3435
- 3. Content • Minimax Decision •Required Pieces for Minimax • Properties of Minimax • Deeper game trees • Alpha-Beta Properties • Alpha-Beta Pruning example • Conclusion
- 4. Minimax Decision • Assigna utility value to each possible ending • Assures best possible ending, assuming opponent also plays perfectly • opponent tries to give you worst possible ending • Depth-first search tree traversal that updates utility values as it recourses back up the tree
- 5. Required Pieces forMinimax • An initial state • The positions of all the pieces • Whose turn it is • Operators • Legal moves the player can make • Terminal Test • Determines if a state is a final state • Utility Function
- 6. Properties of Minimax •Complete? Yes (if tree is finite) • Optimal? Yes (against an optimal opponent) • Time complexity? O(bm) • Space complexity? O(bm) (depth-first exploration
- 7. 7 ED 0B C R 0 N 4 OP 9 Q -6 S 3 T 5 U -7 V -9 K MF G -5 H 3 I 8 J L 2 W -3 X -5 A Deeper Game Trees • Minimax can be generalized for > 2 moves • Values backed up in minimax way terminal states O -5 K 5 M -7 F 4 J 9 E -7 B -5 C 3 A 3 opponent min computer max opponent min computer max
- 8. Alpha-Beta Pruning • Mainidea: Avoid processing subtrees that have no effect on the result • Two new parameters • α: The best value for MAX seen so far • β: The best value for MIN seen so far • α is used in MIN nodes, and is assigned in MAX nodes • β is used in MAX nodes, and is assigned in MIN nodes
- 9. Alpha-Beta Pruning • Alpha= the value of the best choice we’ve found so far for MAX (highest) • Beta = the value of the best choice we’ve found so far for MIN (lowest) • When maximizing, cut off values lower than Alpha • When minimizing, cut off values greater than Beta
- 10. When to Prune •Prune whenever ≥ . • Prune below a Max node whose alpha value becomes greater than or equal to the beta value of its ancestors. • Max nodes update alpha based on children’s returned values. • Prune below a Min node whose beta value becomes less than or equal to the alpha value of its ancestors. • Min nodes update beta based on children’s returned values.
- 11. Properties of α-β •Pruning preserves completeness and optimality of original minimax algorithm • Good move ordering improves effectiveness of pruning • With "perfect ordering," time complexity = O(bm/2) Therefore, doubles depth of search
- 12. Alpha-Beta Example Revisited ,, initial values Do DFS until first leaf =− =+ =− =+ , , passed to kids
- 13. Alpha-Beta Example (continued) MINupdates , based on kids =− =+ =− =3
- 14. Alpha-Beta Example (continued) =− =3 MIN updates , based on kids. No change. =− =+
- 15. Alpha-Beta Example (continued) MAXupdates , based on kids. =3 =+ 3 is returned as node value.
- 16. Alpha-Beta Example (continued) =3 =+ =3 =+ , , passed to kids
- 17. Alpha-Beta Example (continued) =3 =+ =3 =2 MIN updates , based on kids.
- 18. Alpha-Beta Example (continued) =3 =2 ≥ , so prune. =3 =+
- 19. Alpha-Beta Example (continued) 2is returned as node value. MAX updates , based on kids. No change. =3 =+
- 20. Alpha-Beta Example (continued) , =3 =+ =3 =+ , , passed to kids
- 21. Alpha-Beta Example (continued) , =3 =14 =3 =+ MIN updates , based on kids.
- 22. Alpha-Beta Example (continued) , =3 =5 =3 =+ MIN updates , based on kids.
- 23. Alpha-Beta Example (continued) =3 =+ 2 is returned as node value. 2
- 24. Alpha-Beta Example (continued) Maxcalculates the same node value, and makes the same move! 2
- 25. Conclusion • Minimax findsoptimal play for deterministic, fully observable, two-player games • Alpha-Beta reduction makes it faster
- 26.