The document discusses a system for accounting for scalars within the context of linear-algebraic λ-calculus, exploring the relationship between quantum logic and linear logic models. It offers a comprehensive look at concepts such as the no-cloning theorem, linearity restrictions, and the evolution of quantum states as linear operators. The authors aim to contribute to the understanding of quantum computation through the framework of type systems and higher-order computation.













![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
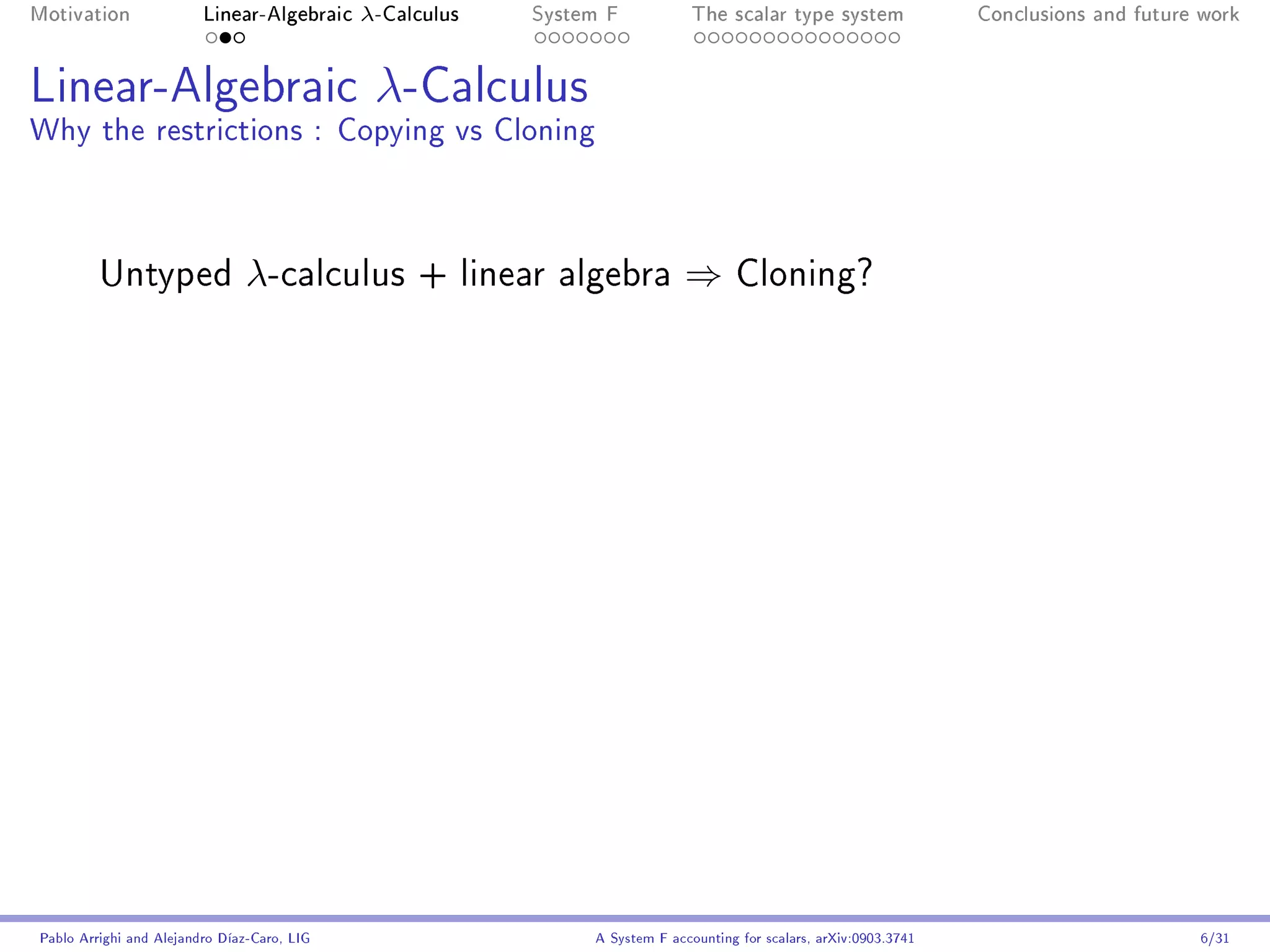
Linear-Algebraic λ-Calculus2
The language
Higher-order computation Linear algebra
t ::= x | λx .t | (t t) | t + t | α.t | 0
λx .t b → t[b/x ] (∗)
(*) b an abstraction or a
variable.
Arrighi, P. and G. Dowek. Linear-algebraic λ-calculus: higher-order,
2
encodings and conuence. Lecture Notes in Computer Science (RTA'08), 5117
(2008), pp. 1731.
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 5/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-14-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
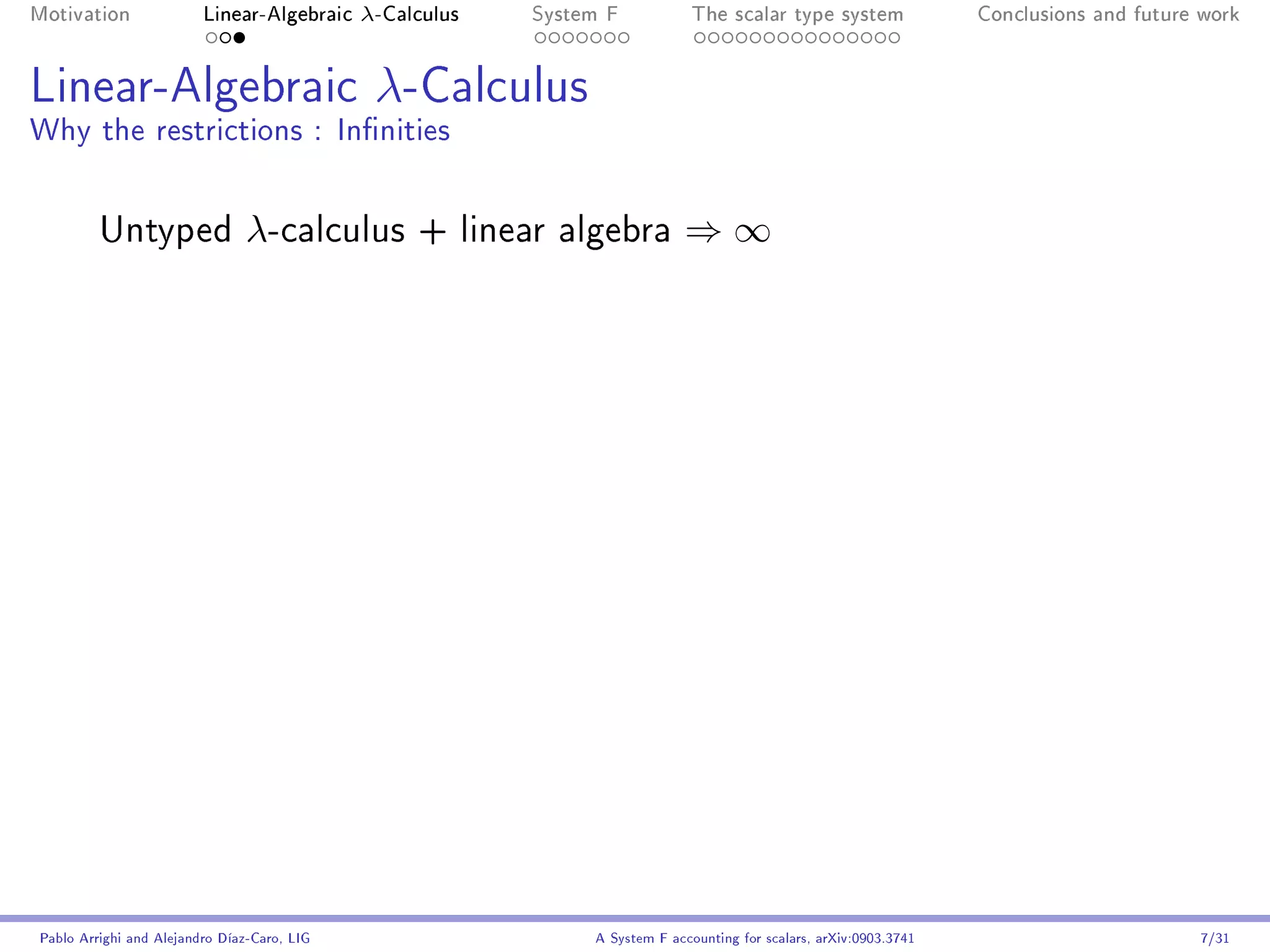
Linear-Algebraic λ-Calculus2
The language
Higher-order computation Linear algebra
t ::= x | λx .t | (t t) | t + t | α.t | 0
λx .t b → t[b/x ] (∗) Elementary rules such as
(*) b an abstraction or a u + 0 → u and
α.(u + v) → α.u + α.v.
variable.
Factorisation rules such as
(**) u closed normal. α.u + β.u → (α + β).u. (**)
(***) u and u + v closed normal.
Application rules such as
u (v + w) → (u v) + (u w).
(***)
Arrighi, P. and G. Dowek. Linear-algebraic λ-calculus: higher-order,
2
encodings and conuence. Lecture Notes in Computer Science (RTA'08), 5117
(2008), pp. 1731.
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 5/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-15-2048.jpg)











![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la
SN : Set of strongly normalising terms
A subset X ∈ SN is saturated if
1 ∀n ≥ 0, (((x t1 ) . . . ) tn ) ∈ X where ti ∈ SN ;
→
− →
−
2 v[b/x ] t ∈ X ⇒ (λx v) b t ∈ X ;
3 t, u ∈ X ⇒ t + u ∈ X ;
4 ∀α, t ∈ X ⇒ α.t ∈ X ;
5 ∀i ∈ I , ((ui w1 ) . . . wn ) ∈ X ⇒ u i w1 . . . w ∈ X ;
n
i ∈I
6 ∀i ∈ I , (u wi ) ∈ X ⇒ u w i ∈ X;
i ∈I
7 α.((t1 t2 ) . . . tn ) ∈ X ⇔ ((t1 t2 ) . . . α.tk ) . . . tn ∈ X (1 ≤ k ≤ n);
8 0 ∈ X;
→
− →
−
9 ∀ t ∈ SN , (0 t ) ∈ X ;
10
→ ∈ SN , (t 0) → ∈ X .
−
∀t, u −u
X stable by construction and anti-reduction
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 9/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-29-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la
SN : Set of strongly normalising terms
A subset X ∈ SN is saturated if
1 ∀n ≥ 0, (((x t1 ) . . . ) tn ) ∈ X where ti ∈ SN ;
→
− →
−
2 v[b/x ] t ∈ X ⇒ (λx v) b t ∈ X ;
3 t, u ∈ X ⇒ t + u ∈ X ;
4 ∀α, t ∈ X ⇒ α.t ∈ X ;
5 ∀i ∈ I , ((ui w1 ) . . . wn ) ∈ X ⇒ u i w1 . . . w ∈ X ;
n
i ∈I
6 ∀i ∈ I , (u wi ) ∈ X ⇒ u w i ∈ X;
i ∈I
7 α.((t1 t2 ) . . . tn ) ∈ X ⇔ ((t1 t2 ) . . . α.tk ) . . . tn ∈ X (1 ≤ k ≤ n);
8 0 ∈ X;
→
− →
−
9 ∀ t ∈ SN , (0 t ) ∈ X ;
10
→ ∈ SN , (t 0) → ∈ X .
−
∀t, u −u
X stable by construction and anti-reduction
SAT is the set of all saturated sets
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 9/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-30-2048.jpg)



![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (III)
Lemma
1 SN ∈ SAT ,
2 A B , ∈ SAT ⇒ A → B ∈ SAT ,
3 For all collection A i of members of SAT ,
i Ai ∈ SAT ,
Denition (Mapping)
[[X ]]ξ = ξ(X ) (where ξ(·) : TVar → SAT )
[[A → B ]]ξ = [[A]]ξ → [[B ]]ξ
[[∀X .T ]]ξ = Y ∈SAT [[T ]]ξ(X :=Y )
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 11/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-34-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (III)
Lemma
1 SN ∈ SAT ,
2 A B , ∈ SAT ⇒ A → B ∈ SAT ,
3 For all collection A i of members of SAT ,
i Ai ∈ SAT ,
Denition (Mapping)
[[X ]]ξ = ξ(X ) (where ξ(·) : TVar → SAT )
[[A → B ]]ξ = [[A]]ξ → [[B ]]ξ
[[∀X .T ]]ξ = Y ∈SAT [[T ]]ξ(X :=Y )
Lemma
Given a valuation ξ , [[T ]]ξ ∈ SAT
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 11/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-35-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (IV)
Denition ( )
For Γ = x1 : A1 , . . . , xn : An , Γ t: T means that ∀ξ ,
x1 ∈ [[A1 ]]ξ , . . . xn ∈ [[An ]]ξ ⇒ t ∈ [[T ]]ξ
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 12/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-36-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (IV)
Denition ( )
For Γ = x1 : A1 , . . . , xn : An , Γ t: T means that ∀ξ ,
x1 ∈ [[A1 ]]ξ , . . . xn ∈ [[An ]]ξ ⇒ t ∈ [[T ]]ξ
Rening the sketch: Prove that Γ t: T ⇒ Γ t: T
We prove this by induction on the derivation of Γ t: T (In fact
the denition of is slightly dierent to strengthen the induction
hypothesis)
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 12/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-37-2048.jpg)


![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (V)
Then, the proof of the strong normalisation theorem is:
Let Γ t: T
⇒ Γ t: T
⇒ If ∀(xi : Ai ) ∈ Γ, xi ∈ [[Ai ]]ξ then t ∈ [[T ]]ξ
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 13/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-40-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (V)
Then, the proof of the strong normalisation theorem is:
Let Γ t: T
⇒ Γ t: T
⇒ If ∀(xi : Ai ) ∈ Γ, xi ∈ [[Ai ]]ξ then t ∈ [[T ]]ξ
Note that
x i ∈ [[Ai ]]ξ because [[Ai ]]ξ is saturated,
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 13/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-41-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Strong normalization of λ2la (V)
Then, the proof of the strong normalisation theorem is:
Let Γ t: T
⇒ Γ t: T
⇒ If ∀(xi : Ai ) ∈ Γ, xi ∈ [[Ai ]]ξ then t ∈ [[T ]]ξ
Note that
x i ∈ [[Ai ]]ξ because [[Ai ]]ξ is saturated,
then t is strong normalising because [[T ]]ξ ⊆ SN
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 13/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-42-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Linear-Algebraic λ-Calculus with λ2la
Higher-order computation Linear algebra
t ::= x | λx .t | (t t) | t + t | α.t | 0
λx .t b → t[b/x ] (∗) Elementary rules such as
(*) b an abstraction or a variable. u + 0 → u and
α.(u + v) → α.u + α.v.
Factorisation rules such as
α.u + β.u → (α + β).u.
Application rules such as
u (v + w) → (u v) + (u w).
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 14/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-43-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Linear-Algebraic λ-Calculus with λ2la
Higher-order computation Linear algebra
t ::= x | λx .t | (t t) | t + t | α.t | 0
λx .t b → t[b/x ] (∗) Elementary rules such as
(*) b an abstraction or a variable. u + 0 → u and
α.(u + v) → α.u + α.v.
Every typable term is strong
normalizing Factorisation rules such as
α.u + β.u → (α + β).u.
Application rules such as
u (v + w) → (u v) + (u w).
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 14/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-44-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Linear-Algebraic λ-Calculus with λ2la
Higher-order computation Linear algebra
t ::= x | λx .t | (t t) | t + t | α.t | 0
λx .t b → t[b/x ] (∗) Elementary rules such as
(*) b an abstraction or a variable. u + 0 → u and
α.(u + v) → α.u + α.v.
Every typable term is strong
normalizing Factorisation rules such as
Hence Yb is no typable! α.u + β.u → (α + β).u.
Application rules such as
u (v + w) → (u v) + (u w).
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 14/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-45-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
System F
Linear-Algebraic λ-Calculus with λ2la
Higher-order computation Linear algebra
t ::= x | λx .t | (t t) | t + t | α.t | 0
λx .t b → t[b/x ] (∗) Elementary rules such as
(*) b an abstraction or a variable. u + 0 → u and
α.(u + v) → α.u + α.v.
Every typable term is strong
normalizing Factorisation rules such as
Hence Yb is no typable! α.u + β.u → (α + β).u.
t − t → 0 always, so it is not Application rules such as
necesary to reduce t rst. we can u (v + w) → (u v) + (u w).
remove the closed-normal
restrictions!
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 14/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-46-2048.jpg)

![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Type inference rules
ax U [ ]
Γ, x : U x :U
Γ u: U → T Γ v: U Γ, x : U t: T
→E → I [U ]
Γ (u v) : T Γ λx t : U → T
Γ u : ∀X .T Γ u: T
∀E [X := U ] ∀I [X ] with X ∈ FV (Γ)
/
Γ u : T [U /X ] Γ u : ∀X .T
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 16/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-48-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Type inference rules
ax U [ ]
Γ, x : U x :U
Γ u: U → T Γ v: U Γ, x : U t: T
→E → I [U ]
Γ (u v) : T Γ λx t : U → T
Γ u : ∀X .T Γ u: T
∀E [X := U ] ∀I [X ] with X ∈ FV (Γ)
/
Γ u : T [U /X ] Γ u : ∀X .T
Γ u: T Γ v: T Γ u: T
ax0 +I αI
Γ 0: T Γ u + v: T Γ α.u : T
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 16/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-49-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Type inference rules
ax U [ ]
Γ, x : U x :U
Γ u : α.(U → T ) Γ v : β.U Γ, x : U t: T
→E → I [U ]
Γ (u v) : (α × β).T Γ λx t : U → T
Γ u : ∀X .T Γ u: T
∀E [X := U ] ∀I [X ] with X ∈ FV (Γ)
/
Γ u : T [U /X ] Γ u : ∀X .T
Γ u : α.T Γ v : β.T Γ u: T
ax +I
0 sI [α]
Γ 0: 0 Γ u + v : (α + β).T Γ α.u : α.T
Where U ∈U and types in contexts are are in U.
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 17/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-50-2048.jpg)








![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Subject reduction proof: example (I)
To show a rule as example, we need some auxiliary lemmas and
denitions:
Order:
Write A B if either
B ≡ ∀X .A or
A ≡ ∀X .C and B ≡ C [U /X ] for some U ∈ U.
≥ is the reexive and transitive closure of .
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 20/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-59-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Subject reduction proof: example (I)
To show a rule as example, we need some auxiliary lemmas and
denitions:
Order:
Write A B if either
B ≡ ∀X .A or
A ≡ ∀X .C and B ≡ C [U /X ] for some U ∈ U.
≥ is the reexive and transitive closure of .
Instuition of this denition:
Types in the numerator of
Γ t: A Γ t : ∀X .C
∀I with X ∈ FV (Γ)
/ or ∀E
Γ t : ∀X .A Γ t : C [U /X ]
are greater than the types in the denominator.
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 20/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-60-2048.jpg)













![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Probabilistic type system: Intuition
Conditional functions → same type on each branch.
By restricting the scalars to positive reals → probabilistic type
system.
For example, one can type functions such as
λx {x [ 1 .(true + false)] [ 4 .true + 3 .false]} : B → B
2
1
4
with the type system serving as a guarantee that the function
conserves probabilities summing to one.
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 24/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-74-2048.jpg)



![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Probabilistic type system: Formalisation
We dene the probabilistic type system to be the scalar type
system with the following restrictions:
S = R+ ,
Contexts: Types in contexts are classic types (C ), i.e. types in
U exempt of any scalar,
We change the rule ∀E to
Γ t : ∀X .T
∀E with C ∈C
Γ t : T [C /X ]
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 25/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-78-2048.jpg)
![Motivation Linear-Algebraic λ-Calculus System F The scalar type system Conclusions and future work
The scalar type system
Probabilistic type system: Formalisation
We dene the probabilistic type system to be the scalar type
system with the following restrictions:
S = R+ ,
Contexts: Types in contexts are classic types (C ), i.e. types in
U exempt of any scalar,
We change the rule ∀E to
Γ t : ∀X .T
∀E with C ∈C
Γ t : T [C /X ]
The nal conclusion must be classic.
Pablo Arrighi and Alejandro Díaz-Caro, LIG A System F accounting for scalars, arXiv:0903.3741 25/31](https://image.slidesharecdn.com/ppstalk-12639017348989-phpapp01/75/A-System-F-accounting-for-scalars-79-2048.jpg)





















