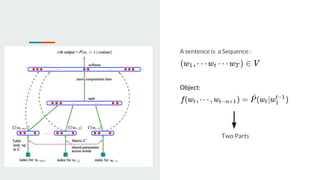
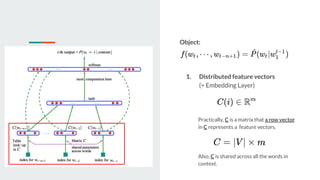
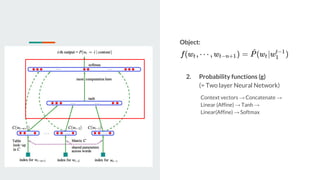
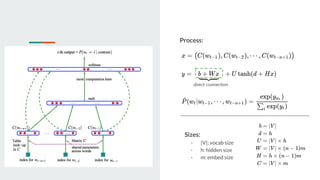
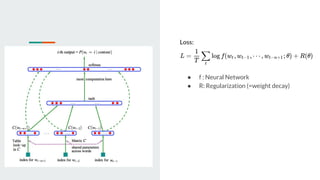
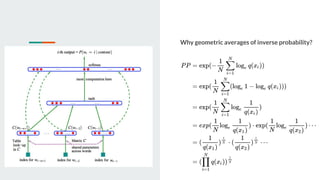
This document discusses neural probabilistic language modeling. It introduces the fundamental problem of language modeling as the curse of dimensionality when using discrete spaces to model language. It then describes statistical language models like n-gram models that estimate the conditional probability of the next word. However, these models have limitations like not handling long-term dependencies beyond 1-2 words. The document proposes a neural probabilistic language model that learns distributed word embeddings to represent words in a continuous vector space. It models the joint probability of word sequences using these embeddings and a neural network, learning the embeddings and probability function simultaneously.

1. A Neural Probabilistic
Language Model
Learning a distributed representation for words
2018.08.09 Soo

2. Contents
● Fundamental Problem of Language Modeling
● Statistical Model of Language
● Neural Probabilistic Language Model
● Result

3. Fundamental Problem of Language Modeling
● Curse of Dimensionality
○ As the number of features or dimensions grows, the amount of data that we need to generalize
accurately exponentially
Number of free parameters
when using discrete spaces
to modeling languages
Use Continuous Space !!

4. Statistical Model of Language
● The conditional probability of the next word given all the previous ones
● The reason of approximation:
○ Temporally closer words in the word sequence are statistically more dependent → N-gram Models

5. Statistical Model of Language
● N-gram models examples
○ How likely is “University” given “New York”?
○ Count all “New York University”
○ Count all “New York ?”: e.g., “New York State”, “New York City”, “New York Fire”, “New York Police”,
“New York Bridges”, …
○ How often “New York University” happens among these?

6. Problems in Statistical Model of Language
● A new combination of n words appears that was not seen in the training corpus
● Solutions
○ back-off trigram models (Katz, 1987)
○ smoothed(or interpolated) trigram model (Jelinek and Mercer, 1980)
● Limits
○ Long-term dependency: no farther than 1 or 2 words
○ no measure of similarity

7. Neural Probabilistic Language Model
● Abstract:
○ Associate with each word in the vocabulary a distributed word feature vector (a real valued vector
in
○ express the joint probability function of word sequences in terms of the feature vectors of these
words in the sequence
○ learn simultaneously the word feature vectors and the parameters of that probability function

8. Neural Probabilistic Language Model
1. Word Feature Vector
○ associated with a point in a vector space (embed word into a vector space)
○ Dimension of vector m is much more smaller than the vocabulary size ( V )
2. Probability function
○ product of conditional probabilities → maximization of log-likelihood

9. A sentence is a Sequence :
Object:
Two Parts

10. Object:
1. Distributed feature vectors
(= Embedding Layer)
Practically, C is a matrix that a row vector
in C represents a feature vectors.
Also, C is shared across all the words in
context.

11. Object:
2. Probability functions (g)
(= Two layer Neural Network)
Context vectors → Concatenate →
Linear (Affine) → Tanh →
Linear(Affine) → Softmax

12. Process:
Sizes:
- |V|: vocab size
- h: hidden size
- m: embed size

13. Loss:
● f : Neural Network
● R: Regularization (=weight decay)

14. Parameters:
Total number of free parameters:
- h: hidden size
- m: embed size
Sizes:
- |V|: vocab size
- h: hidden size
- m: embed size

15. Test Measurement: Perplexity
A measurement of how well a probability
distribution or probability model (q) predicts a
sample
Lower Perplexity means the model q fits better to
generate training data. Means that model is less
surprised by the test sample.

16. Why geometric averages of inverse probability?

17. Result

18. References
● A Neural Probabilistic Language Model - Yoshua Bengio, 2003
blog: https://simonjisu.github.io
github: https://github.com/simonjisu