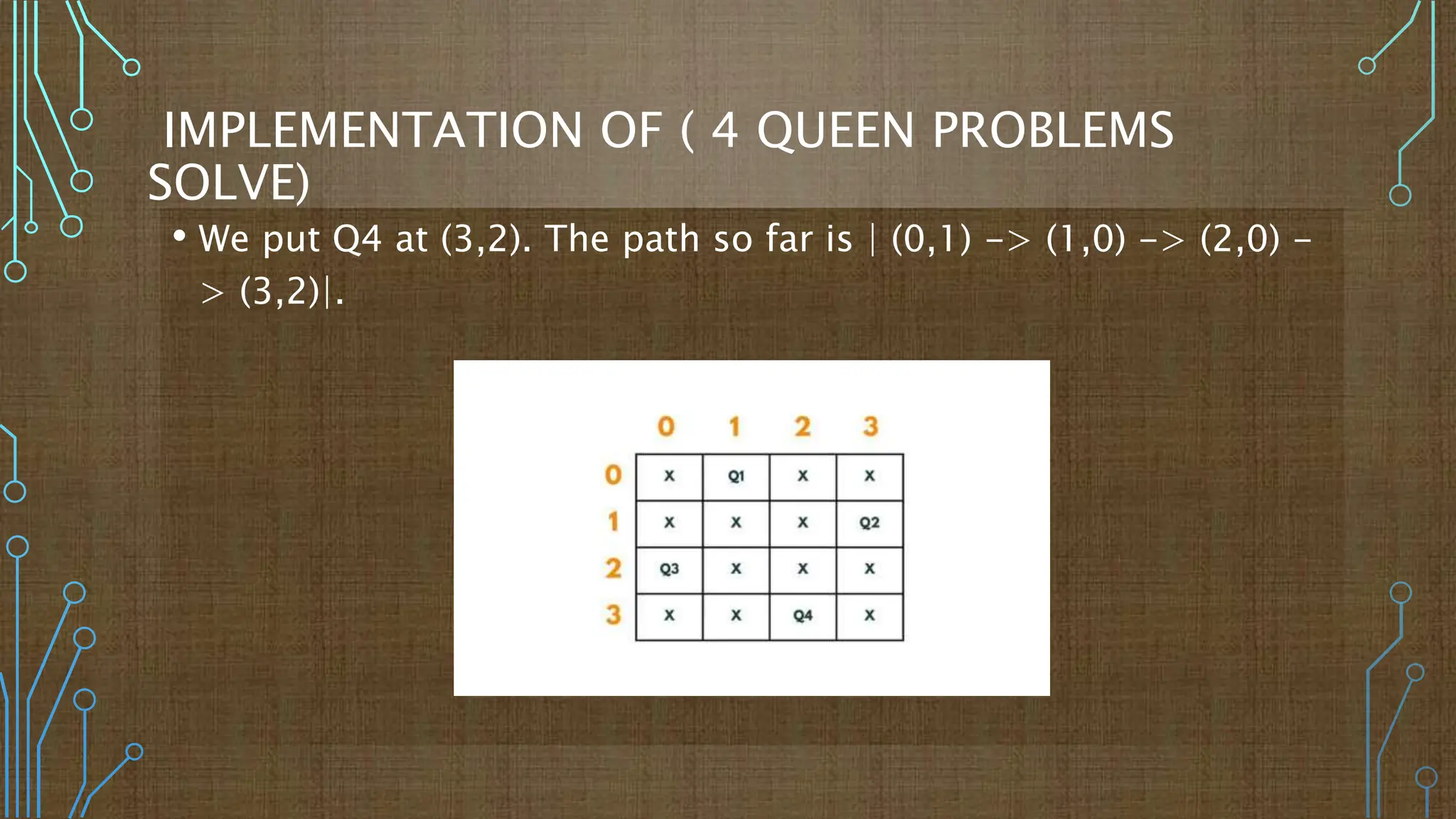
The n-queens problem is a classic puzzle where the objective is to place n queens on an n×n chessboard without any two queens threatening each other. The solution often utilizes backtracking, a method where one explores potential placements of queens, retracing steps if conflicts arise. An example implementation using a 4x4 chessboard demonstrates this backtracking process to find valid arrangements of queens.

1. The N-Queens problem
 The N-Queens problem is a classic puzzle that's commonly framed as a chessboard
problem. The objective is to place N chess queens on an N×N chessboard in such a way
that no two queens threaten each other; that is, no two queens share the same row,
column, or diagonal. The problem was first formulated in 1848 by the chess player Max
Bezzel and later popularized by Franz Nauck in 1850.

2. The N-Queens problem
 N Queen problem demands us to place N queens on a N x N chessboard so that
no queen can attack any other queen directly.
Problem Statement: We need to find out all the possible arrangements in which N
queens can be seated in each row and each column so that all queens are safe.
The queen moves in 8 directions and can directly attack in these 8 directions only. N
Queen problem demands us to place N queens on a N x N chessboard so that no
queen can attack any other queen directly.
Problem Statement: We need to find out all the possible arrangements in which N
queens can be seated in each row and each column so that all queens are safe.
The queen moves in 8 directions and can directly attack in these 8 directions only.

3. The N-Queens problem


4. WHAT IS BACKTRACKING?
• Let's understand it through an example. Imagine you want to go to a grocery store,
but you somehow forget the path and end up at a crossroads. You know that one of
the paths is certainly going to take you to the store. What would you do in such a
situation? Explore each path one by one.Well, that's the only option you have. So, you
will choose one of the paths and start searching for the store. If the store is not
found on path 1 you go back from where you started and explore other paths. This
kind of concept is called backtracking. So, in backtracking we try out one of the
moves out of the available moves and try to solve the problem with the selected
move. If the problem does get solve we print the solution else we explore all the
other moves. And if no move leads you to the solution, we declare that the problem
has no solution. Here are some of the other more popular Backtracking problems to
understand the importance of it.
 Use this Backtracking method to solve N Queen
Problems.

5. WHAT IS
BACKTRACKING?

6. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• This problem demands us to put 4 queens on 4 X 4 chessboard
in such a way that one queen is present in each row and
column and no queen can attack any other queen directly. this
means no 2 or more queens can be placed in the same diagonal
or row or column.

7. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Let's try to put queens Q1, Q2, Q3, and Q4 in the above present
chessboard. The first queen i.e. Q1 can be put anywhere on the
chessboard as there is no other queen present on the board
and hence no restrictions. Therefore putting Q1 at position
(0,0). So the path so far is| (0,0)|.

8. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• When Q1 has been placed there are some places where the next
queens can't be placed to fulfill given conditions. So to put
queen Q2 in the second row we have positions - (1,2) and (1,3).
Let's put it at (1,2).The path so far is | (0,0) -> (1,2)|

9. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Now this placement of Q2 blocks all the boxes of row 3 and
hence there is no way to put Q3. If we put it at (2,0) or (2,2), Q1
will attack it, and at (2,1) and (2,3) Q2 attacks it. Therefore we
backtrack from here and revisit the previous solution by
readjusting the position of Q2. So instead of putting it at (1,2),
we put it at (1,3). The path so far is | (0,0) -> (1,3)|

10. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• We put Q3 at (2,1). Hence, the path so far is | (0,0) -> (1,3) ->
(2,1)|.

11. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Now again the same problem occurs, there left no box to place
Q4. There was only 1 way to place Q3 and all placements of Q2
have been explored, so now we come to Q1 for re-adjustment.
We move it from (0,0) to (0,1). The path so far is | (0,1)|.

12. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• We put Q2 at (1,0). The path so far is | (0,1) -> (1,0)|.

13. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Q3 is put at (2,2). The path so far is | (0,1) -> (1,0) -> (2,2)|.

14. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Now again there is no space left for placement of Q4 in row 4.
Therefore we again backtrack and readjust position of Q2 from
(1,0) to (1,3).The path so far is | (0,1) -> (1,3)|.

15. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Q3 is put at (2,0). The path so far is | (0,1) -> (1,0) -> (2,0)|.

16. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• We put Q4 at (3,2). The path so far is | (0,1) -> (1,0) -> (2,0) -
> (3,2)|.

17. IMPLEMENTATION OF ( 4 QUEEN PROBLEMS
SOLVE)
• Therefore through backtracking, we reached a solution where 4
queens are put in each row and column so that no queen is
attacking any other on a 4 X 4 chessboard.
• Another solution can be:

18. ( 4 QUEEN
PROBLEMS CODE IN
PYTHON)

19. 4 QUEEN
PROBLEMS
OUTPUT WITH 2
SOLUTIONS.