Документ описывает алгоритмы криптосистем на эллиптических кривых, включая ECDSA и EC Diffie-Hellman, а также стандарты ГОСТ для этих технологий. Рассматриваются этапы генерации ключей, подписи и проверки, а также условия для корректности выполнения алгоритмов. Упоминаются конкретные параметры и условия для использования, такие как ограничения на параметры эллиптической кривой и хэш-функции.

1. Семинар № 8
Криптосистемы на
эллиптических кривых
Колыбельников Александр

2. Содержание
•
•
•
•
EC DSA
EC Diffe-Hellman
ГОСТ 34.10-2001
ГОСТ 34.10-2012

3. ECDSACurve Digest Signature
Алгоритм ЭЦП ECDSA (Elliptic
Algorithm) принят в качестве стандартов ANSI X9F1 и
IEEE P1363. В германии является государственным.
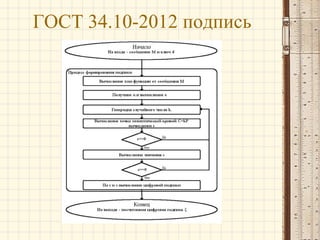
Алгоритм генерации:
1) Выбираем эллиптическую кривую E, определённую на
Число точек в E ( Z p ) должно делиться на большое
целое Z p .
2) Выбираем точку P ∈ E ( Z p )порядка n.
n.
3) Выбираем случайное число
4) Вычисляем d ∈ [ 1, n − 1] .
Q ∈ dP.
5) Секретным ключом объявляем d,
открытым – ( E , P, n, Q).

4. ECDSA - подпись
1) Выбираем случайное число k ∈ [ 1, n − 1] .
2) Вычисляем
kP = ( x1 , y1 );
r = x1 mod n.
Если r ≠ 0, переходим к шагу 3, в противном
случае возвращаемся к шагу 1.
k −1 mod n.
3) Вычисляем
s = k −1 (h( M ) + dr ) mod n.
4) Вычисляем
Если s ≠ 0, переходим к шагу 5, в противном
случае возвращаемся к шагу 1.
5) Подписью под сообщением M является пара
целых чисел (r , s).

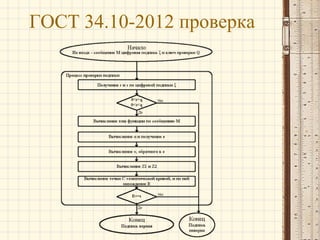
5. ECDSA - проверка
1) Если r и s – целые числа,
принадлежащие к интервалу [1, n − 1],
переходим к шагу 2, в противном случае
w = s −1 mod n
%
h( M ).
считаем, что подпись некорректна.
1) Вычисляем
% ) w mod n; и
u = h( M
2) Вычисляем u = rw mod n.
3) Вычисляем u1 P + u2Q = ( x0 , y0 );
v = x0 mod n.
4) Подпись верна в том и только том случае,
когда v = r.
1
2

6. Проверка
1) В качестве хэш-функции h( x) на шаге 4
вычисления подписи в стандартах ANSI
X9F1 и IEEE P1364 использовался SHA-1.
s
2) При r = 0
результат вычисления d не
зависит от секретного ключаs = 0.
3) При s −1 mod n необходимого для проверки
подписи числа
не существует.

7. EC Diffe-Hellman
• Выбираем эллиптическую кривую и
случайную точку G на ней
• Алиса: Находим точку Ga=aG
• Боб: Точку Gb=bG
• Боб: Секретную точку K=bGa
• Алиса и Боб: aGb=a(bG)=(ab)G
• =b(aG)=bGa

8. ГОСТ Р 34.10-2001
• Размер подписи – 512 бит; 3
4a
255
J ( E ) = 1728 3
(mod p)
• p>2
2
4a + 27b
•
4a 3 + 27b 2 ≠ 0(mod p)
• m - порядок группы точек эллиптической
кривой, m ≠ p
• q - порядок подгруппы m = nq и 2254 < q < 2256
h( M )
•
- ГОСТ Р = 1..B
p t ≠ 1(mod q ) ∀t 34.11-94.
J (E ) ≠ 0
• J ( E ) ≠ 1728
, где
B ≥ 31

9. ГОСТ Р 34.10-2012
• Выбираем модуль p > 2255
• Ограничения на кривую:
4a 3
J ( E ) = 1728 3
(mod p ) 4a 3 + 27b 2 ≠ 0(mod p )
4a + 27b 2
• Порядок группы точек m должен быть
отличен от p
• Хеш-функция- h( M )
• d –ключ шифрования из диапазона
0<d<q

10. ГОСТ 34.10-2012 подпись

11. ГОСТ 34.10-2012 подпись
•
•
•
•
•
E= z mod q,
Генерация случайного k из 0<k<q
Вычисление C=kP r=x mod q
Нахождение s=(rd+ke) modq
Подпись (r,s)

12. ГОСТ 34.10-2012 проверка

13. ГОСТ 34.10-2012 проверка
• E= z mod q,
• V = e-1mod q
• Вычисление z1=sv mod q, z2= -rv mod q
• Нахождение C=z1P +z2 Q , R=x mod q
• Проверка R=r

14. Спасибо за внимание!