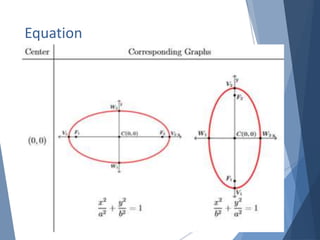
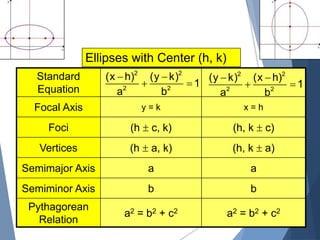
The document defines and describes key properties of ellipses, including that an ellipse is the set of all points where the sum of distances from two fixed foci is a constant. It provides the standard equation forms for ellipses with horizontal and vertical major axes when the center is at (0,0), and then extends this to ellipses with an arbitrary center (h,k). Key properties defined include the lengths of the semi-major and semi-minor axes, the distance between the center and foci, and the Pythagorean relationship between these values. Examples are given to assess understanding of writing the standard equation for an ellipse given properties like the vertices and foci.

1. Ellipse with V(h,k)
Application of Ellipse

2. Ellipse
The ellipse is the set of all points on
the plane for which the sum of
distances from two fixed points (foci)
is a positive constant.

3. Parts of an Ellipse:
 Semi-axis - ½ the length of axis
 Center - midpoint of the segment joining the foci
 Vertices - endpoints of the major axis. The points on the ellipse which lie on the
line containing the foci
 Major axis – The line segment joining the vertices, longer axis, contains foci
 Co- Vertices – the points on the ellipse which are on the perpendicular bisector
of the major axis
 Minor axis – The line segment joining the co-vertices, shorter axis
 Latus Rectum - The line segment passing through the focus and perpendicular to
the major axis
 Foci - two given fixed points on the major axis
Center Focus
Focus

4. Equation

5. Ellipse with horizontal major axis:
• Center is (0, 0).
• Length of major axis is 2a.
• Length of minor axis is 2b.
• Distance between center and either focus
is c with c2 = a2– b2, a > b > 0.

6. Ellipse with vertical major axis:
• Center is (0, 0).
• Length of major axis is 2a.
• Length of minor axis is 2b.
• Distance between center and either focus
is c with c2 = a2– b2, a > b > 0.
• LR = 2b2/a
• e = c/a
• d = a/e = a2/c

7. Problem:

9. Ellipse with horizontal major axis:
• Center is (h, k).
• Length of major axis is 2a.
• Length of minor axis is 2b.
• Distance between center
• and either focus
is c with c2 = a2– b2, a > b
> 0.

10. Ellipse with vertical major axis:
• Center is (h, k).
• Length of major axis is 2a.
• Length of minor axis is 2b.
• Distance between center
and either focus
is c with c2 = a2– b2, a > b
> 0.

11. Pre-
Calculus
Ellipses with Center (h, k)
Standard
Equation
Focal Axis y = k x = h
Foci (h  c, k) (h, k  c)
Vertices (h  a, k) (h, k  a)
Semimajor Axis a a
Semiminor Axis b b
Pythagorean
Relation
a2 = b2 + c2 a2 = b2 + c2
 
 
2 2
2 2
(x h) (y k)
1
a b
 
 
2 2
2 2
(y k) (x h)
1
a b

12. ASSESSMENT
 1. What is the standard form of the
ellipse that has vertices at (0, ±3) and foci
at ( 0, ±2)?
 2. What is the standard form of equation
of the ellipse that has vertices (-2, -8) and
(-2, 2) and foci (-2, -7) and (-2, 1).?