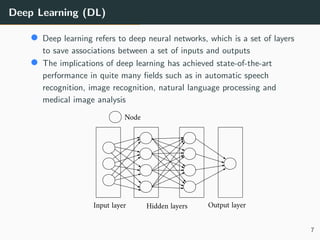
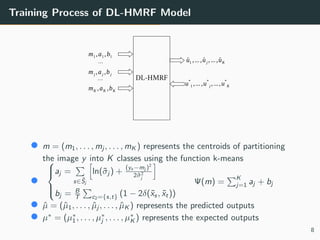
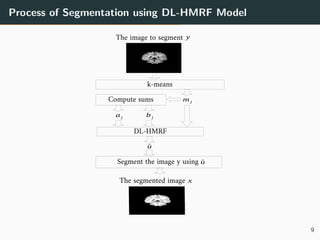
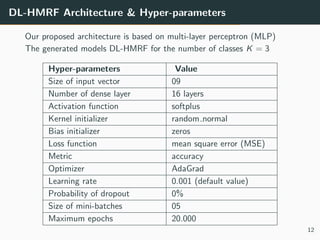
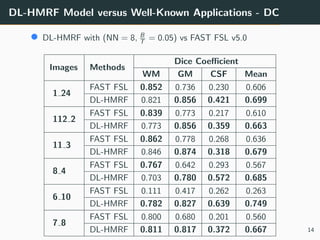
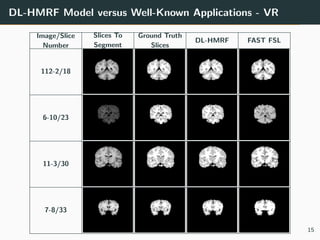
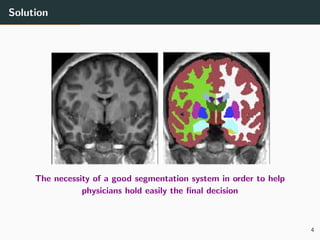
The document presents a 3D brain image segmentation model using deep learning and hidden Markov random fields (HM_RF), developed to aid physicians in analyzing imaging data. The study includes details on the model's conception, experimental results, and a comparison with existing methods, showing promising performance, particularly in segmentation quality. However, the training time for the model remains high, suggesting the potential use of Kubernetes clusters to optimize this aspect in the future.

1. AICCSA 2020 ACS/IEEE International Conference on Computer Systems and Applications
3D Brain Image Segmentation Model using
Deep Learning and Hidden Markov Random
Fields
EL-Hachemi Guerrout, Ramdane Mahiou, Anfel Melouk,
Ines Harmali
November 2nd to November 5th, 2020
Laboratoire
1

2. 1. Introduction
2. Hidden Markov Random Field
3. Deep Learning (DL)
4. Conception of the New Model (DL-HMRF)
5. Experimental Results
6. Conclusions & Perspectives
2

3. Introduction

4. Problematic
We face a huge amount of data produced
by imaging devices
Manual analysis and interpretation is
a tedious task
3

5. Solution
The necessity of a good segmentation system in order to help
physicians hold easily the final decision
4

6. Hidden Markov Random Field

7. Hidden Markov Random Field
The image to segment y = {ys}s∈S
into K classes is a realization of Y
• Y = {Ys}s∈S is a family of random
variables
• ys ∈ [0 . . . 255]
The segmented image into K classes
x = {xs}s∈S is realization of X
• X = {Xs}s∈S is a family of random
variables
• xs ∈ {1, . . . , K}
An example of segmentation into
K = 4 classes
x∗
= argx∈Ω max {P[X = x | Y = y]}
5

8. Hidden Markov Random Field
• This elegant model leads to the optimization of an energy function
Ψ(x, y) = s∈S ln(σxs
) +
(ys −µxs )2
2σ2
xs
+ β
T c2={s,t} (1 − 2δ(xs, xt))
• Our way to look for the minimization of Ψ(x, y) is to look for the
minimization Ψ(µ), µ = (µ1, . . . , µK ) where µi are means of gray
values of class i
Ψ(µ) =
K
j=1
s∈Sj
[ln(σj ) +
(ys −µj )2
2σ2
j
] + β
T
c2={s,t}
(1 − 2δ(xs, xt))
6

9. Deep Learning (DL)

10. Deep Learning (DL)
• Deep learning refers to deep neural networks, which is a set of layers
to save associations between a set of inputs and outputs
• The implications of deep learning has achieved state-of-the-art
performance in quite many fields such as in automatic speech
recognition, image recognition, natural language processing and
medical image analysis
7

11. Conception of the New Model
(DL-HMRF)

12. Training Process of DL-HMRF Model
• m = (m1, . . . , mj , . . . , mK ) represents the centroids of partitioning
the image y into K classes using the function k-means
•



aj =
s∈ ˜Sj
ln(˜σj ) +
(ys −mj )2
2˜σ2
j
bj = B
T c2={s,t} (1 − 2δ(˜xs, ˜xt))
Ψ(m) =
K
j=1 aj + bj
• ˆµ = (ˆµ1, . . . , ˆµj , . . . , ˆµK ) represents the predicted outputs
• µ∗
= (µ∗
1, . . . , µ∗
j , . . . , µ∗
K ) represents the expected outputs
8

13. Process of Segmentation using DL-HMRF Model
9

14. Experimental Results

15. DC - The Dice Coefficient
The Dice coefficient measures how much
the segmentation result is close to the
ground truth
DC =
2|A ∩ B|
|A ∪ B|
a. DC equals 1 in the best case
(perfect segmentation)
b. DC equals 0 in the worst case
(every pixel is misclassified)
The Dice Coefficient
10

16. Context of Training and Tests
Environment
JetBrains PyCharm Community Edition 2018.3.1
Computer with intel core I7 2.50 GHz CPU, 8GO RAM
Microsoft Windows 10
IBSR
We have used IBSR images in our tests and to prepare training data-set
They are twenty magnetic resonance brain images with modality =
T1-weighted and dimension 256 × 256 × Z, Z ∈ {58, 59, 61, 62, 63, 64}
The ground-truth images are available
We have dedicated 14 IBSR images to train our models
The rest (six images) are devoted to the tests
11

17. DL-HMRF Architecture & Hyper-parameters
Our proposed architecture is based on multi-layer perceptron (MLP)
The generated models DL-HMRF for the number of classes K = 3
Hyper-parameters Value
Size of input vector 09
Number of dense layer 16 layers
Activation function softplus
Kernel initializer random normal
Bias initializer zeros
Loss function mean square error (MSE)
Metric accuracy
Optimizer AdaGrad
Learning rate 0.001 (default value)
Probability of dropout 0%
Size of mini-batches 05
Maximum epochs 20.000
12

18. Proposed Models
• The performance of DL-HMRF model is very sensitive to HMRF
parameters that are: B
T and the number of neighbors (NN)
• In total, we have created six models with different values of
parameters B
T ∈ {0.05, 0.1, 0.25, 2} and NN ∈ {4, 6, 8}
• Through the results
- Training time is considerable
- the model with B
T = 0.05 and NN = 8 gives the best results
Models
NN = 4, B
T = 0.05
NN = 4, B
T = 0.1
NN = 4, B
T = 0.25
NN = 4, B
T = 2
NN = 6, B
T = 0.05
NN = 8, B
T = 0.05
13

19. DL-HMRF Model versus Well-Known Applications - DC
• DL-HMRF with (NN = 8, B
T = 0.05) vs FAST FSL v5.0
Images Methods
Dice Coefficient
WM GM CSF Mean
1 24
FAST FSL 0.852 0.736 0.230 0.606
DL-HMRF 0.821 0.856 0.421 0.699
112 2
FAST FSL 0.839 0.773 0.217 0.610
DL-HMRF 0.773 0.856 0.359 0.663
11 3
FAST FSL 0.862 0.778 0.268 0.636
DL-HMRF 0.846 0.874 0.318 0.679
8 4
FAST FSL 0.767 0.642 0.293 0.567
DL-HMRF 0.703 0.780 0.572 0.685
6 10
FAST FSL 0.111 0.417 0.262 0.263
DL-HMRF 0.782 0.827 0.639 0.749
7 8
FAST FSL 0.800 0.680 0.201 0.560
DL-HMRF 0.811 0.817 0.372 0.667 14

20. DL-HMRF Model versus Well-Known Applications - VR
Image/Slice
Number
Slices To
Segment
Ground Truth
Slices
DL-HMRF FAST FSL
112-2/18
6-10/23
11-3/30
7-8/33
15

21. Conclusions & Perspectives

22. Conclusion & Perspective
• Through the achieved results, we could say that the DL-HMRF
model is very promising in the quality of segmentation
• Nevertheless, the training time is still considerable. As a perspective,
Kubernetes clusters can be used to reduce the training time
16

23. Thank you for your attention
16

24. Questions?
16