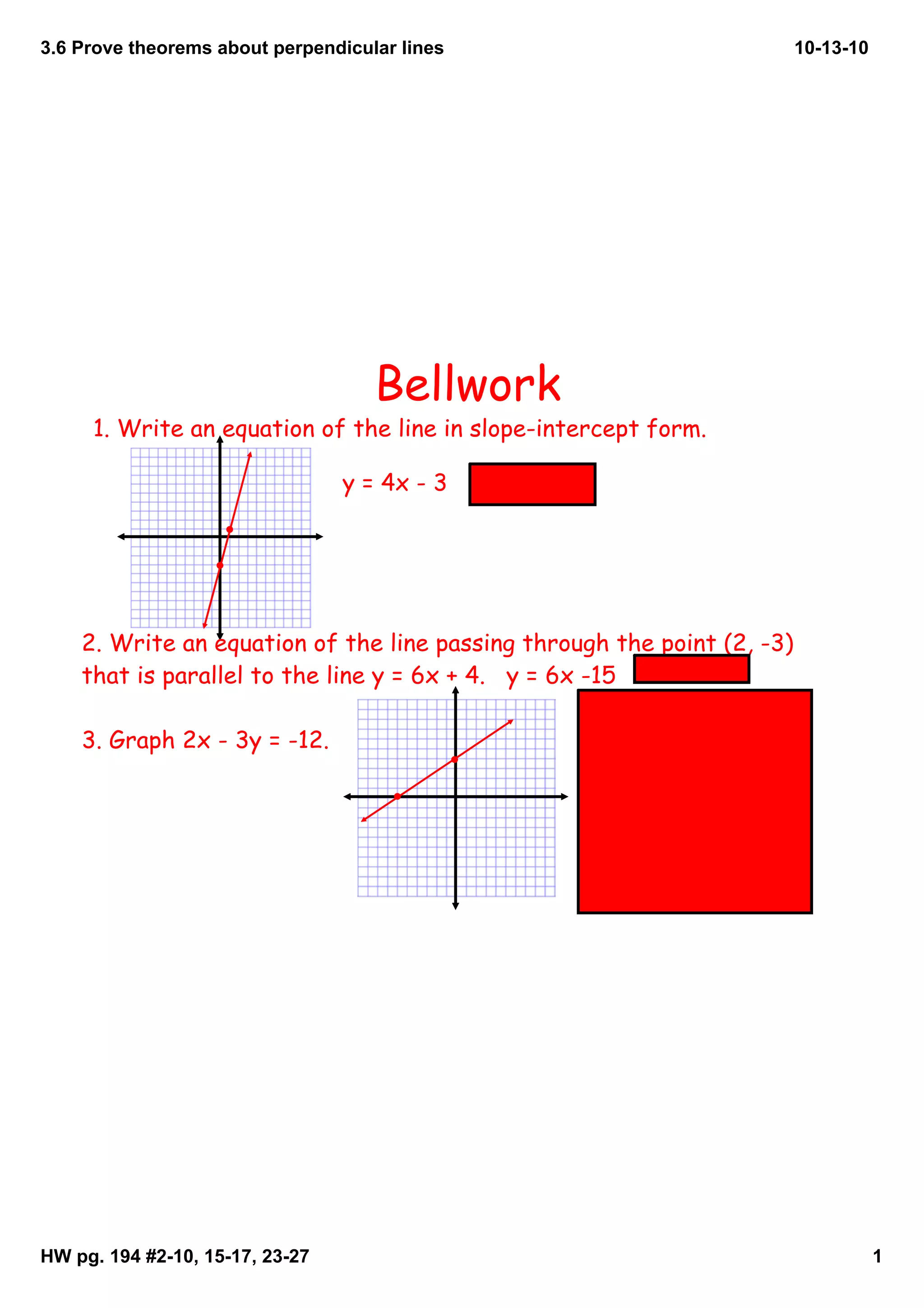
This document discusses several theorems about perpendicular lines: - If two lines intersect to form congruent angles, then the lines are perpendicular. - If two lines are perpendicular, then they intersect to form four right angles. - If two sides of two adjacent acute angles are perpendicular, then the angles are complementary. - If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line. - If two lines are perpendicular to the same line, then they are parallel to each other. The document also discusses how to find the distance between a point and a line, and the distance between two parallel lines. It provides an example problem for finding

1. 3.6 Prove theorems about perpendicular lines 10­13­10
Bellwork
1. Write an equation of the line in slope-intercept form.
y = 4x - 3
2. Write an equation of the line passing through the point (2, -3)
that is parallel to the line y = 6x + 4. y = 6x -15
3. Graph 2x - 3y = -12.
HW pg. 194 #2­10, 15­17, 23­27 1

2. 3.6 Prove theorems about perpendicular lines 10­13­10
3.6 Prove Theorems about Perpendicular Lines
Theorem 3.8: If 2 lines intersect to form a linear pair of congruent angles,
then the lines are perpendicular.
If <1 ≅ <2, then g h. 1 2
Theorem 3.9: If 2 lines are perpendicular,
then they intersect to form 4 right angles.
1 2
If a b, then <1,<2,<3 & <4 are right <s.
4 3
HW pg. 194 #2­10, 15­17, 23­27 2

3. 3.6 Prove theorems about perpendicular lines 10­13­10
Theorem 3.10: If 2 sides of 2 adjacent acute angles are perpendicular,
then the angles are complementary.
If BA BC, then <1 & <2 are complementary. 1
2
HW pg. 194 #2­10, 15­17, 23­27 3

4. 3.6 Prove theorems about perpendicular lines 10­13­10
Theorem 3.11: Perpendicular Transversal Theorem
If a transversal is to 1 of 2 // lines,
then it is to the other line.
j
h
If h // k and j h, then j k.
k
Theorem 3.12: Lines Perpendicular to a Transversal Theorem
If 2 lines are to the same line,
then they are // to each other.
m n
If m p & n p, then m // n. p
HW pg. 194 #2­10, 15­17, 23­27 4

5. 3.6 Prove theorems about perpendicular lines 10­13­10
HW
pg. 194
#2­10 & 15­17
HW pg. 194 #2­10, 15­17, 23­27 5

6. 3.6 Prove theorems about perpendicular lines 10­13­10
Distance from a Point to a Line: length of perpendicular segment
from point to the line.
A
Distance btwn point A & line k = AB
k
B
Distance between 2 Parallel Lines: length of any perpendicular
segment joining the 2 lines.
C m
Distance btwn line p & line m = CD
p
D
Distance Formula: √ 2 ­ x1)2 + (y2 ­ y1)2
(x
Example
What is the distance between the two parallel lines?
(4,6)
Step 1: Find slope of 1st line. (0,3) (7,2)
(3,­1)
Step 2: Write equation of 1st line.
Step 3: Write equation of line to 1st line through 2nd line
Step 4: Find intersection of 1st line and line.
Step 5: Find distance between // lines using point of intersection and the
chosen point from step 3.
HW pg. 194 #2­10, 15­17, 23­27 6

7. 3.6 Prove theorems about perpendicular lines 10­13­10
HW pg. 194 #2­10, 15­17, 23­27 7

8. 3.6 Prove theorems about perpendicular lines 10­13­10
Class Assignment
pg. 195
#23­27
HW pg. 194 #2­10, 15­17, 23­27 8