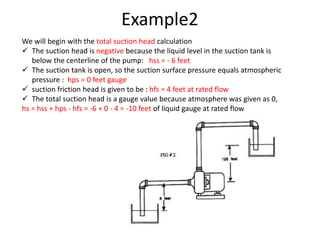
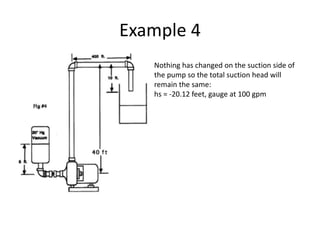
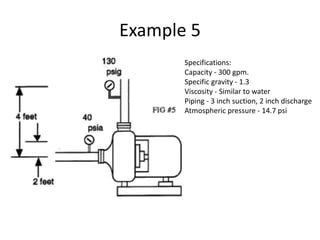
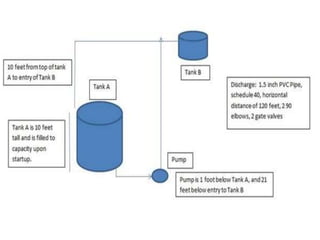
The document discusses how to calculate total dynamic head (TDH) in an industrial pumping system. TDH is comprised of vertical rise and friction loss. It is important to accurately calculate TDH to properly size pumping equipment. To calculate TDH: 1) Determine the vertical rise between the liquid's starting and ending points, assuming an empty tank for the worst case. 2) Calculate friction losses of all pipe and components the liquid encounters on discharge. 3) Add the vertical rise and friction losses together to obtain the total dynamic head. An example calculation is provided to demonstrate determining TDH for 25 GPM flowing from a pump to Tank B.

1. Pump Design
Fundamentals and Basic information

2. Head Calculations
• Capacity is measured in gal/min. (Volumetric
flow rate)
• we can easily calculate the lb/min being
pumped. (mass flow rate) [ How?]
• Head or height is measured in feet
• If we multiply these two together we get:
ft-Ib/min which converts directly to work as
33,000 ft-Ib/min = 1 hp

3. • Pressure is not as convenient a term because
the amount of pressure that the pump will
deliver depends upon
 the weight (specific gravity) of the liquid being pumped and
the specific gravity changes with
 temperature
 type of fluid
 fluid concentration

4. • Note that static head is always measured from the center line of the pump to the
highest liquid level
• To calculate head accurately we must calculate the total head on both the suction
and discharge sides of the pump
• In addition to the static head we will learn that there is a head caused by resistance
in the piping, fittings and valves called friction head
• head caused by any pressure that might be acting on the liquid in the tanks
including atmospheric pressure, called " surface pressure head".
• we will then subtract the suction head from the discharge head and the amount
remaining will be the amount of head that the pump must be able to generate at
the rated flow

5. • System head = total discharge head - total suction head
H = hd - hs
• The total discharge head is made from three separate heads:
hd = hsd + hpd + hfd
hd = total discharge head
hsd = discharge static head
hpd = discharge surface pressure head
hfd = discharge friction head
• The total suction head also consists of three separate heads
hs = hss + hps - hfs
hs = total suction head
hss = suction static head
hps = suction surface pressure head
hfs = suction friction head

6. • As we make these calculations, you must sure
that all calculations are made in either "feet of
liquid gauge" or "feet of liquid absolute". In
case you have forgotten "absolute means that
you have added atmospheric pressure (head)
to the gauge reading.

7. Example2
We will begin with the total suction head calculation
 The suction head is negative because the liquid level in the suction tank is
below the centerline of the pump: hss = - 6 feet
 The suction tank is open, so the suction surface pressure equals atmospheric
pressure : hps = 0 feet gauge
 suction friction head is given to be : hfs = 4 feet at rated flow
 The total suction head is a gauge value because atmosphere was given as 0,
hs = hss + hps - hfs = -6 + 0 - 4 = -10 feet of liquid gauge at rated flow

8. The Total Discharge Head Calculation
Example 2
 The static discharge head is: hsd = 125 feet
 The discharge tank is also open to atmospheric
pressure, thus: hpd = 0 feet gauge
 discharge friction head is given as hfd = 25 feet at rated
flow
 The total discharge head is:
hd = hsd + hpd + hfd = 125 + 0 + 25 = 150 feet of liquid
gauge at rated flow
• The total system head calculation:
• H = hd - hs = 150 - (-10)= 160 feet of liquid at rated
flow

9. Example 3
Specifications:
1. Transferring 1000 gpm. weak acid from
the vacuum receiver to the storage tank
2. Specific Gravity - 0.98
3. Viscosity - equal to water
4. Piping - All 6" Schedule 40 steel pipe
5. Discharge piping rises 40 feet vertically
above the pump centerline and then
runs 400 feet horizontally. There is one
90° flanged elbow in this line
6. Suction piping has a square edge inlet,
four feet of pipe, one gate valve, and one
90° flanged elbow all of which are 6" in
diameter.
7. The minimum level in the vacuum
receiver is 5 feet above the pump
centerline.
8. The pressure on top of the liquid in the
vacuum receiver is 20 inches of mercury,
vacuum

10. To calculate suction surface pressure
use one of the following formulas
• inches of mercury x 1.133/ specific gravity =
feet of liquid
• pounds per square inch x 2.31/specific gravity
= feet of liquid
• Millimeters of mercury / (22.4 x specific
gravity)
= feet of liquid

11. Total suction head calculation
• 1. The suction side of the system shows a
minimum static head of 5 feet above suction
centerline. Therefore, the static suction head
is:
• hss = 5 feet2. Using the first conversion
formula, the suction surface pressure is:
• hps = -20 Hg x 1.133/ 0.98 = -23.12 feet gauge

12. The suction friction head, hfs
FITTING K FROM TABLE
6" Square edge inlet 0.50 32 (a)
6" 90 flanged elbow 0.29 32 (a)
6" Gate valve 0.11 32 (b)
equals the sum of all the friction losses in the suction line.
Friction loss in 6" pipe at 1000 gpm from table 15 of the
Hydraulic Institute Engineering Data Book, is 6.17 feet per 100 feet of pipe.
in 4 feet of pipe friction loss = 4/100 x 6.17 = 0.3 feet
Friction loss coefficients (K factors) for the inlet,
elbow and valve can be added together and multiplied by the velocity head
Total coefficient, K = 0.90
Total friction loss on the suction side is:
hfs = 0.3 + 1.7 = 2.0 feet at 1000 gpm.4. The total suction head then becomes:
hs = hss + hps - hfs = 5 + (-23.12) - 2.0 = -20.12 feet, gauge at 1000 gpm

13. Total discharge head calculation
1. Static discharge head = hsd = 40 feet
2. Discharge surface pressure = hpd = 0 feet gauge
3. Discharge friction head = hfd = sum of the following losses :
• Friction loss in 6" pipe at 1000 gpm. from table 15, is 6.17 feet per hundred feet of
pipe. In 440 feet of pipe the friction loss = 440/100 x 6.17 = 27.2 feet
• Friction loss in 6" elbow:
• from table 32 (a), K = 0,29
• from table 15, V2/2g = 1.92 at 1000 gpm.
• Friction loss = K V2/2g = 0.29 x 1.92 = 0.6 feet
• The friction loss in the sudden enlargement at the end of the discharge line is
called the exit loss. In systems of this type where the area of the discharge tank is
very large in comparison to the area of the discharge pipe, the loss equals V2/2g,
as shown in table 32 (b).
• Friction loss at exit = V2/2g = 1.9 feet
• The discharge friction head is the sum of the above losses, that is:
• hfd = 27.2 + 0.6 + 1.9 = 29.7 feet at 1000 gpm.

14. • 4. The total discharge head then becomes:
• hd = hsd + hpd + hfd = 40 + 0 + 29.7 = 69.7
feet, gauge at 1000 gpm.c. Total system head
calculation:
• H = hd - hs = 69.7 - (-20.2) = 89.9 feet at 1000
gpm.

15. Example 4
Nothing has changed on the suction side of
the pump so the total suction head will
remain the same:
hs = -20.12 feet, gauge at 100 gpm

16. Total discharge head calculation
• 1. The static discharge head "hsd" will change from 40 feet
to 30 feet, since the highest liquid surface in the discharge
is now only 30 feet above the pump centerline.(This value
is based on the assumption that the vertical leg in the
discharge tank is full of liquid and that as this liquid falls it
will tend to pull the liquid up and over the loop in the pipe
line. This arrangement is called a siphon leg).
• 2. The discharge surface pressure is unchanged:
• hpd = 0 feet
• 3. The friction loss in the discharge pipe will be increased
by the additional 10 feet of pipe and the additional elbow.

17. • 3. The friction loss in the discharge pipe will
be increased by the additional 10 feet of pipe
and the additional elbow.
• In 10 feet of pipe the friction loss = 10/100 x
6.17 = 0.6 feet
• The friction loss in the additional elbow = 0.6
feet
• The friction head will then increase as follows:
• hfd = 29.7 + 0.6 + 0.6 = 30.9 feet at 1000 gpm

18. The total discharge head becomes
• hd = hsd + hpd + hfd
• = 30 + 0 + 30.9
• = 60.9 feet, gauge at 1000 gpm.
• 5. Total system head calculation
• H = hd - hs = 60.9 - (-20.12) = 81 feet at 1000
gpm

19. Example 5
Specifications:
Capacity - 300 gpm.
Specific gravity - 1.3
Viscosity - Similar to water
Piping - 3 inch suction, 2 inch discharge
Atmospheric pressure - 14.7 psi

20. • Divide the heads into two sections again:
• The discharge gauge head corrected to the centerline of the
pump, in feet of liquid absolute is found by adding the
atmospheric pressure to the gauge reading to get absolute
pressure, and then converting to absolute head:
• hgd = (130 + 14.7) x 2.31 / (1.3 Specific Gravity) + 4 = 261.1
feet, absoluteNote the 4 foot head correction to the pump
centerline.
• The discharge velocity head at 300 gpm. is found in table 9
of the Hydraulic Institute Engineering Data Book
• hvd = 12.8 feet at 300 gpm.

21. • The suction gauge reading is in absolute terms so it
needs only to be converted to feet of liquid, absolute.
• hgs = 40 x 2.3 / 1.3 +2 = 73.08 feet absolute
• Note the 2 foot head correction to the pump
centerline.
• The suction velocity head at 300 gpm. is found in table
11 of the Pipe Friction Manual:
• hvs = 2.63 feet at 300 gpm.
• The total system head developed by the pump =:
• H = (hgd + hvd ) - ( hgs + hvs ) = (261.1 + 12.8) - (73.08 +
2.6)= 198.22 feet absolute at 300 gpm.

25. • How to Calculate Total Dynamic Head for an Industrial Pump
• Posted: 5/19/2016
• Back
•
Total Dynamic Head in an industrial pumping system is the total amount of pressure when water is flowing in a system. It is comprised of two parts: the vertical rise and friction loss.
• It is important to calculate this accurately in order to determine the correct sizing and scale of pumping equipment for your needs.
• To calculate Total Dynamic Head, also known as TDH, we need to calculate two things:
A) The Vertical Rise.
B) The Friction Losses of all the pipe and components the liquid encounters on the discharge of the pump.
C) After calculating both, add them together to calculate TDH.
• Let us show you how to calculate these together and then you will be able to complete this on your own! For the purpose of this walkthrough, we will determine the Total Dynamic Head
for 25GPM to go from the Pump to Tank B in the example below.
• How to Calculate Vertical Rise
• A) Vertical Rise. It must be determined what the vertical rise is from the liquid’s starting point to its ending point. As the liquid level in the tank decreases, the vertical rise will increase,
and consequently, the total dynamic head will increase. To simplify matters, assume the tank is empty for the worst case situation.
•
•
• In the above example, if Tank A is full and going to the top of Tank B, the vertical rise is 10 feet. If Tank A is half empty and there is only 5 feet of liquid in Tank A, then the vertical rise is
15 feet. If tank A is entirely emptied, then the vertical rise will be 21 feet. With the vertical rise being anywhere from 10-21 feet, it is easiest just to use 21 feet to be on the safe side
unless you are certain the liquid level will not go below a certain height.
• How to Calculate Friction Loss
• B) Friction Loss. To calculate the friction loss you first need to know what your desired flow is. Each flow rate will have a different friction loss. The more flow going thru a pipe, the
more friction loss there will be, so 5GPM going thru 1 inch pipe will have a higher friction loss than 1GPM going thru 1 inch pipe. After your flow rate, you need to know what type of pipe
you are using, the schedule of the pipe, and the length of the pipe, both vertically and horizontally. You also need to know how many elbows, valves, connections, and anything else that
comes into contact with the liquid.
• Using the above example, let’s calculate the friction loss for 25GPM. There is 1.5 inch PVC Schedule 40 pipe. The horizontal pipe distance from the pump to Tank B is 120 feet, and the
vertical pipe distance from the pump to the tank B is 21 feet. There are 2 90 degree long radius elbows and 2 gate valves.
• Once this information is calculated, take the following steps:
• Step 1) Add the horizontal and vertical discharge pipe together.
120 feet+21 feet= 141 feet
• Step 2) Go to this website: http://www.freecalc.com/fricfram.htm
Step 3) Enter pipe size, pipe schedule, piping material, piping length, valves, and fittings.
• For this example, the numbers are:
1.5 Inch, Schedule 40, PVC Material, 141 Piping Length in Feet, 2 90 LR Elbows, and 2 Gate Valves.
Step 4) Press “Calculate Pressure Drop.” After pressing “Calculate Pressure Drop,” the calculator states the head loss is 5.6 feet.
• Some of our preferred resources:
• Sta-Rite Pipe Friction Loss Charts
• University of Wisonsin Total Dynamic Head Calculator
•
• The Result: Total Dynamic Head Calculation
• C) Total Dynamic Head. The worst case scenario for the vertical rise is 21 feet. The friction loss for 25GPM is 5.6 feet. Adding these two numbers together, the Total Dynamic Head is
26.6 feet for 25GPM to go from the Pump to Tank B.
•
• Alternative Scenario