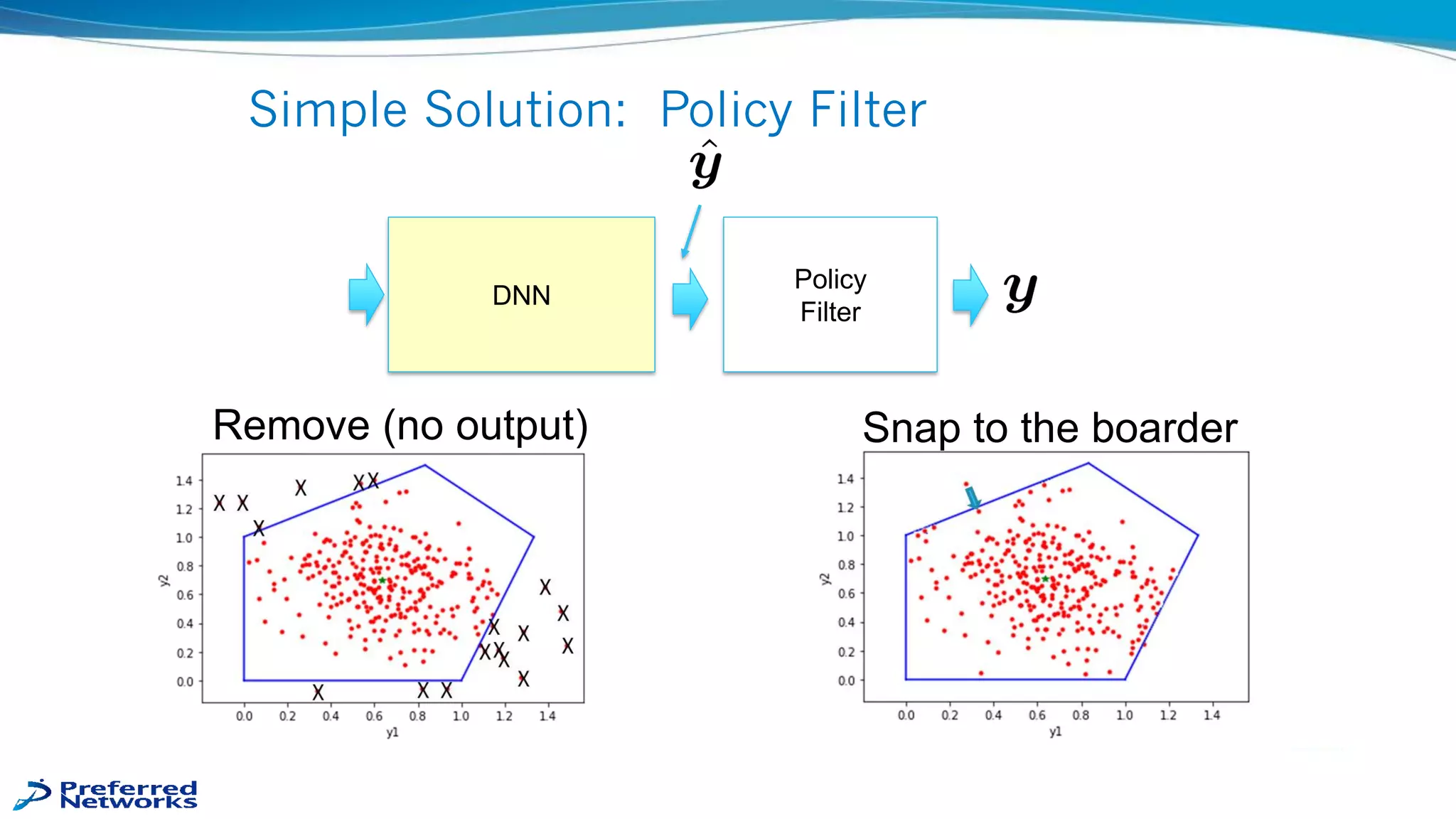
1) Deep neural networks can output any point in space but this is problematic when outputs must remain within a defined feasible region. 2) The presentation proposes transforming the output space to guarantee outputs fall within the feasible region. This is done by bounding the space to a hypercube around a pivot point, then shrinking/extending points toward the origin while keeping the pivot interior. 3) With this transformation, the output is guaranteed to remain feasible for any model parameters or inputs, allowing training to continue while enforcing constraints.

1. Guaranteeing Deep Neural Network
Outputs in a Feasible Region
Hiroshi Maruyama
PFN Fellow

2. 2
What is “invariance” in ML?

3. 3
Fundamental Limitation of Machine Learning :
It’s Statistics!
Original Distribution
i. i. d.
Training Data Set
Trained Model
Random
Sampling !!
No guarantee of “100% correctness”

4. 4
In deep learning, any point in the Rn is possible as output
Input
Output：A Point in Rn
For any point P in Rn, there is a combination of
the input, training data set, hyper-parameters,
and random-number seed that generates P
• Training Data Set
• Hyper parameters
• Random # seeds
• … and program itself

5. 5
Example: Controlling a Drone
DL ModuleSensor Input
Reference Point
How to Guarantee that the reference point is always in the region?

6. 6
Definition: Feasible Region and Non-Feasible Solutions
Feasible Region
Non-feasible
solutions
We assume the feasible region is convex

7. DNN
Policy
Filter
Simple Solution: Policy Filter
Remove (no output) Snap to the boarder

8. Proposed Solution: Transformation of Output Space
Rn → Rn Space
Transformation
Select an interior point (called pivot)

9. Step 1 (Bounding) : Transform Rn to n-dimensional
hypercube
9
Sigmoid Function
Apply Sigmoid on each dimension
Move the pivot to the origin of the hypercube

10. Step 2: Shrink / Extend every point towards the origin
10

11. 11
Step 3: Finally move the pivot to the original position
For any combination of the input, training data set, hyper parameters, and
random number seed, the output is guarantted to be feasible

12. Proposed transformation works for any “star-shaped” space
12
Make this x0 the pivot
Set S is Star-shaped iff there is x0 s.t. for any interior point x,
the line segment xx0 ∈ S

13. Teacher signals can be given in the transformed space
Original DNN
(parameters to be
trained)
Transformation to
Feasible Region
(fixed parameters)
Back propagation
Rn Space
Input
Feasible Region
Teacher
Signal
loss

14. 14
Thank You
Twitter: @maruyama