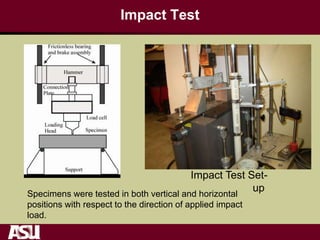
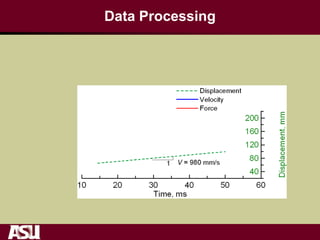
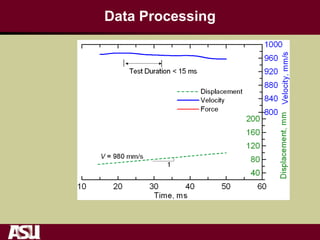
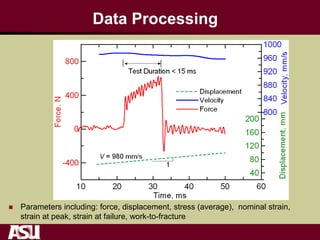
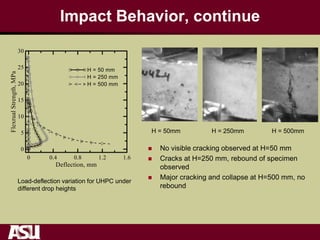
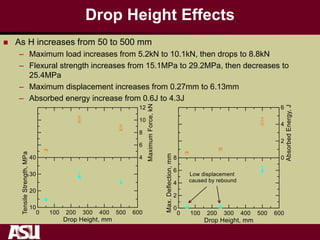
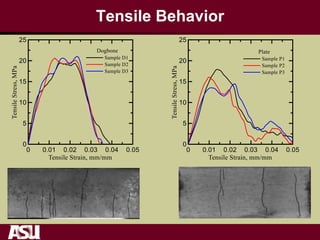
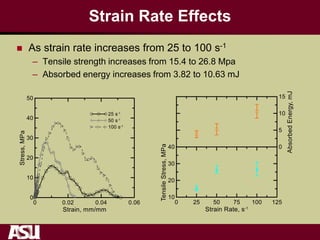
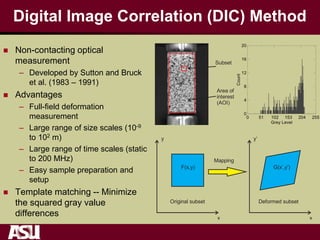
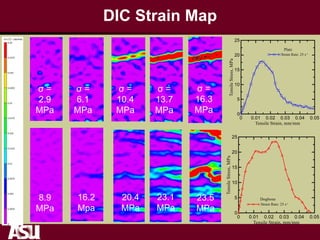
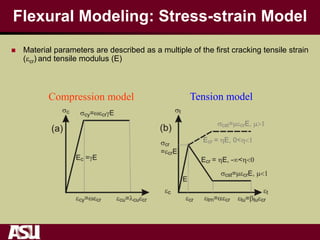
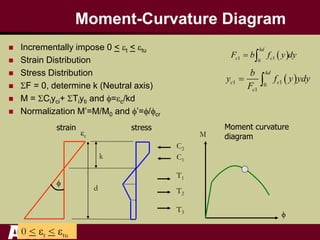
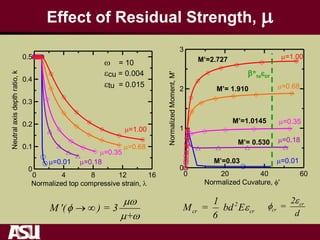
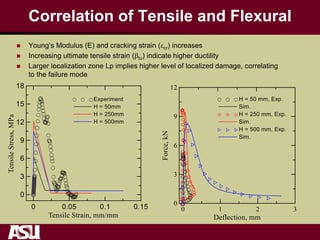
This document summarizes research on the tensile and flexural behavior of ultra-high performance concrete (UHPC) under high-speed and impact loads. High-speed testing systems were used to apply tensile and flexural impact loads to UHPC specimens. Digital image correlation was utilized to analyze crack propagation and strain fields. The research found that UHPC achieved tensile strengths over 20 MPa and flexural strengths exceeding 25 MPa. An analytical model was also developed that could predict UHPC's flexural impact response based on parameters like residual strength, localization zone size, and tensile and flexural properties.

1. Tensile and Flexural Behavior of UHPC under High-
Speed Tensile and Impact Loads
Barzin Mobasher, Yiming Yao, Flavio A. Silva, Vikram Dey
School of Sustainable Engineering and the Built Environment
Ira A. Fulton Schools of Engineering
Arizona State University
Tempe, AZ 85287-5306
ACI Fall Convention, October, 2014, Washington DC
UHPC Behavior under Blast and Impact Load Effects

2. Outline
 Introduction
 Testing Methodology and Data Processing
 Flexural Impact Behavior
 Tensile Behavior
 Digital Image Correlation (DIC) Method
 Analytical Modelling of Flexural Response
 Summary

3. Introduction
 Desire of energy-efficient, environment
friendly, sustainable, resilient
 Ultra-high performance concrete (UHPC)
– 150 Mpa (22 ksi)
– 6% steel fibers
– High strength
– Low permeability
 Strength, ductility, impact resistance,
durability, aggressive environmental and
chemical resistance
 Thin sections
 Complex structural forms
 Cast by pouring, injection, extrusion

4. Impact, Blast, Dynamic Events
 Cases for dynamic loading:
– blast explosions
– projectiles
– earthquakes
– fast moving traffic
– wind gusts, wind driven objects,
– machine vibrations.
 Inherent brittleness and low tensile
strength, dynamic loading can cause
severe damage.
 Mechanical properties at high strain
rates for analysis of structural
components.

5. Experimental Program
Materials Weight per
litter, g
Cement-I 832
Microsilica Elkem
971
135
Silica fume 207
Water 166
Sand 975
SAP 29.4
Steel fiber (2.5%) 192
Mix Design
Beam specimen for flexural impact
Dogbone
Specimen
for
tension
Plate
specimen
for
tension

6. High speed testing system at ASU
MTS servo-hydraulic system, rate
up to 14 m/s, load capacity: 90 kN
Dogbone sample Plate sample

7. Impact Test
Impact Test Set-
up
Specimens were tested in both vertical and horizontal
positions with respect to the direction of applied impact
load.

8. High Speed Image Acquisition

9. Data Processing

10. Data Processing

11. Data Processing
 Parameters including: force, displacement, stress (average), nominal strain,
strain at peak, strain at failure, work-to-fracture

12. Frequency Analysis and Low-pass filter
Design
100 1000 10000
Frequency (Hz)
0
0.005
0.01
0.015
0.02
0.025
FourierAmplitude(g-s)
Hammer
Raw Signal
Filtered Signal
Modal analysis tests were conducted to identify the predominant
frequencies of the hammer and the test specimens. The predominant
frequency of the hammer is about 5 kHz
0.05 0.052 0.054 0.056 0.058 0.06
Time, sec
-400
-200
0
200
400
600
Acceleration,g
Acceleration of Specimen
h = 50.8 mm
Vertical Direction
Raw Data
Filtered Data

13. Impact Behavior
0 0.02 0.04 0.06 0.08
Time, sec
-400
0
400
800
Acceleration,g
Acceleration of ARG6B
h = 50 mm
h = 200 mm
h = 250 mm
Acceleration and Impact force for UHPC specimens at different drop heights

14. Impact Behavior, continue
Load-deflection variation for UHPC under
different drop heights
H = 50mm H = 250mm H = 500mm
 No visible cracking observed at H=50 mm
 Cracks at H=250 mm, rebound of specimen
observed
 Major cracking and collapse at H=500 mm, no
rebound

15. Drop Height Effects
 As H increases from 50 to 500 mm
– Maximum load increases from 5.2kN to 10.1kN, then drops to 8.8kN
– Flexural strength increases from 15.1MPa to 29.2MPa, then decreases to
25.4MPa
– Maximum displacement increases from 0.27mm to 6.13mm
– Absorbed energy increase from 0.6J to 4.3J

16. Tensile Behavior

17. Strain Rate Effects
 As strain rate increases from 25 to 100 s-1
– Tensile strength increases from 15.4 to 26.8 Mpa
– Absorbed energy increases from 3.82 to 10.63 mJ

18. Digital Image Correlation (DIC) Method
 Non-contacting optical
measurement
– Developed by Sutton and Bruck
et al. (1983 – 1991)
 Advantages
– Full-field deformation
measurement
– Large range of size scales (10-9
to 102 m)
– Large range of time scales (static
to 200 MHz)
– Easy sample preparation and
setup
 Template matching -- Minimize
the squared gray value
differences
Subset
Area of
interest
(AOI)
Original subset Deformed subset
F(x,y) G(x’,y’)
x
y
x’
y’
Mapping

19. DIC Strain Map
σ =
2.9
MPa
σ =
6.1
MPa
σ =
10.4
MPa
σ =
13.7
MPa
σ =
16.3
MPa
8.9
MPa
16.2
Mpa
20.4
MPa
23.1
MPa
23.5
MPa

20. Crack Width Measurement
-0.14
-0.253
-0.37
-0.49
-0.60
-0.72
-0.83
-0.95
-1.07
V (mm)
5.0
4.4
3.8
3.1
2.5
1.9
1.3
0.6
0.0
yy (%)

21. Flexural Modeling: Stress-strain Model
Tension modelCompression model
 Material parameters are described as a multiple of the first cracking tensile strain
(cr) and tensile modulus (E)

22. Stress and Strain Distribution
0 < β < 1 and λ < ω 1 < β < α and λ < ω
α < β < βtu and λ < ω

23. Moment-Curvature Diagram
M
f
f
c
0 < t < tu
k
d
C2
T1
T2
T3
C1
stressstrain Moment curvature
diagram
 Incrementally impose 0 < t < tu
 Strain Distribution
 Stress Distribution
 SF = 0, determine k (Neutral axis)
 M = SCiyci+ STiyti and f=c/kd
 Normalization M’=M/M0 and f’=f/fcr
 1 10
kd
c cF b f y dy 
 1 10
1
kd
c c
c
b
y f y ydy
F
 

24. Localization Rules
Moment
Curvature
M0
Mmax
Mfail
fj,Mj)
fj-1,Mj-1)
Loading
Unloading
Non-Localized
Zone
Localized
Zone
S S/2
cS
P Localized
Zone
Non-Localized
Zone
Axis of
Symmetry
1
1
( )j j
j j
M M
EI
f f 



 
• Flexural specimen is loaded beyond the peak strength;
• Distinct zones develop as the deformation localizes in the
cracking region an average response over the crack spacing
region ;
• Results are used as a smeared crack in conjunction with the
moment–curvature diagram
• Measurement from DIC

25. Effect of Residual Strength, m
0 4 8 12 16
Normalized top compressive strain, 
0
0.1
0.2
0.3
0.4
0.5
Neutralaxisdepthratio,k
m=0.01
m=0.35
m=0.68
m=1.00
m=0.18
 = 10
cu = 0.004
tu = 0.015
0 20 40 60
Normalized Cuvature, f'
0
1
2
3
NormalizedMoment,M'
m=0.01
m=0.35
m=0.68
m=1.00
m=0.18
cr
cr
2
=
d

f2
cr cr
1
M = bd E
6
M '( ) = 3
+
m
f
m 
 
M’= 1.910
M’=1.0145
M’= 0.530
M’=2.727
M’=0.03
*tucr

26. Effect of Localization Zone Size, Lp
• Affects the general softening behavior in the post
peak zone
• The simulated residual load capacity is not
sensitive
• Model parameters:
• b=40mm, h=40mm, L=125mm
• E=45GPa, cr=280m, a90, h0.011, m0.021,
tu300, g0.95, 8.33, cu27
~5mm
Localization
Shear
lagUniform

27. Simulation of Experiment Results
• Other model
parameters:
• g0.95, 8.33,
cu27
Drop height
(mm)
E (Gpa) cr (m) m h a tu Lp (mm)
50 35 180 0.11 -0.010 90 280 5
250 45 270 0.02 -0.011 90 300 5
500 42 250 0.06 -0.010 95 500 20

28. Correlation of Tensile and Flexural
 Young’s Modulus (E) and cracking strain (cr) increases
 Increasing ultimate tensile strain (tu) indicate higher ductility
 Larger localization zone Lp implies higher level of localized damage, correlating
to the failure mode

29. Summary
 High speed tensile and flexural impact test procedures for UHPC were
developed
 Tensile strength over 20 MPa was obtained and the flexural strength
exceeded 25 MPa
 Crack and failure behaviours were characterized by means of high
speed images
 Digital image correlation (DIC) method was used to determine the
inhomogeneous displacement/strain fields
 An optical method of crack width measurement using DIC is proposed
 Bilinear parametric model was able to predict the flexural impact
responses

30. Thank You!