Recommended
PDF
2015年度秋学期 応用数学(解析) 第12回 複素関数・正則関数 (2015. 12. 10)
PDF
2015年度秋学期 応用数学(解析) 第15回 ルベーグ積分 (2016. 1. 21)
PDF
2015年度秋学期 応用数学(解析) 第14回 ルベーグ測度と完全加法性 (2016. 1. 14)
PDF
2015年度秋学期 応用数学(解析) 第4回 収束とは何か,ε-δ論法 (2015. 10. 22)
PDF
2014年度秋学期 応用数学(解析) 第5部・測度論ダイジェスト / 第15回 ルベーグ積分 (2015. 1. 22)
PDF
2015年度秋学期 応用数学(解析) 第1回 イントロダクション (2015. 9. 24)
PDF
2014年度秋学期 応用数学(解析) 第5部・測度論ダイジェスト / 第14回 ルベーグ測度と完全加法性 (2015. 1. 15)
PDF
2014年度秋学期 応用数学(解析) 第4部・複素関数論ダイジェスト / 第12回 複素関数・正則関数 (2014. 12. 18)
PDF
2016年度秋学期 応用数学(解析) 第15回 ルベーグ積分 (2017. 1. 19)
PDF
2014年度秋学期 応用数学(解析) 第4部・複素関数論ダイジェスト / 第13回 孤立特異点と留数 (2015. 1. 8)
PDF
2016年度秋学期 応用数学(解析) 第11回 振動と微分方程式 (2016. 12. 8)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第12回 複素関数論(1) 複素関数・正則関数 (2018. 12. 11)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第13回 複素関数論(2) 孤立特異点と留数 (2018. 12. 18)
PDF
2016年度秋学期 応用数学(解析) 第8回 2階線形微分方程式(2) (2016. 11. 24)
PDF
2016年度秋学期 応用数学(解析) 第12回 複素関数・正則関数 (2016. 12. 15)
PDF
2016年度秋学期 応用数学(解析) 第10回 生存時間分布と半減期 (2016. 12. 1)
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第8回 2階線形微分方程式(2) (2018. 11. 13)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第14回 測度論(1) ルベーグ測度と完全加法性 (2019. 1. 8)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第15回 測度論(2) ルベーグ積分 (2019. 1. 15)
PDF
2016年度秋学期 応用数学(解析) 第13回 孤立特異点と留数 (2016. 12. 22)
PDF
2013年度春学期 画像情報処理 第13回「CTスキャナ ― 投影からの画像の再構成/Radon変換と投影定理」
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第7回 2階線形微分方程式(1) (2018. 11. 6)
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第6回 変数分離形の変形 (2018. 10. 30)
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第5回 微分方程式とは・変数分離形 (2018. 10. 23)
PDF
2016年度秋学期 画像情報処理 第13回 Radon変換と投影定理 (2017. 1. 12))
PDF
2016年度秋学期 応用数学(解析) 第2回 無限にも大小がある (2016. 10. 6)
PDF
2016年度秋学期 応用数学(解析) 第7回 2階線形微分方程式(1) (2016. 11. 17)
PDF
2016年度秋学期 応用数学(解析) 第4回 収束とは何か,ε-δ論法 (2016. 10. 20)
PDF
2022年度秋学期 応用数学(解析) 第13回 複素関数論ダイジェスト(2) 孤立特異点と留数 (2022. 12. 22)
PDF
More Related Content
PDF
2015年度秋学期 応用数学(解析) 第12回 複素関数・正則関数 (2015. 12. 10)
PDF
2015年度秋学期 応用数学(解析) 第15回 ルベーグ積分 (2016. 1. 21)
PDF
2015年度秋学期 応用数学(解析) 第14回 ルベーグ測度と完全加法性 (2016. 1. 14)
PDF
2015年度秋学期 応用数学(解析) 第4回 収束とは何か,ε-δ論法 (2015. 10. 22)
PDF
2014年度秋学期 応用数学(解析) 第5部・測度論ダイジェスト / 第15回 ルベーグ積分 (2015. 1. 22)
PDF
2015年度秋学期 応用数学(解析) 第1回 イントロダクション (2015. 9. 24)
PDF
2014年度秋学期 応用数学(解析) 第5部・測度論ダイジェスト / 第14回 ルベーグ測度と完全加法性 (2015. 1. 15)
PDF
2014年度秋学期 応用数学(解析) 第4部・複素関数論ダイジェスト / 第12回 複素関数・正則関数 (2014. 12. 18)
What's hot
PDF
2016年度秋学期 応用数学(解析) 第15回 ルベーグ積分 (2017. 1. 19)
PDF
2014年度秋学期 応用数学(解析) 第4部・複素関数論ダイジェスト / 第13回 孤立特異点と留数 (2015. 1. 8)
PDF
2016年度秋学期 応用数学(解析) 第11回 振動と微分方程式 (2016. 12. 8)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第12回 複素関数論(1) 複素関数・正則関数 (2018. 12. 11)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第13回 複素関数論(2) 孤立特異点と留数 (2018. 12. 18)
PDF
2016年度秋学期 応用数学(解析) 第8回 2階線形微分方程式(2) (2016. 11. 24)
PDF
2016年度秋学期 応用数学(解析) 第12回 複素関数・正則関数 (2016. 12. 15)
PDF
2016年度秋学期 応用数学(解析) 第10回 生存時間分布と半減期 (2016. 12. 1)
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第8回 2階線形微分方程式(2) (2018. 11. 13)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第14回 測度論(1) ルベーグ測度と完全加法性 (2019. 1. 8)
PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第15回 測度論(2) ルベーグ積分 (2019. 1. 15)
PDF
2016年度秋学期 応用数学(解析) 第13回 孤立特異点と留数 (2016. 12. 22)
PDF
2013年度春学期 画像情報処理 第13回「CTスキャナ ― 投影からの画像の再構成/Radon変換と投影定理」
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第7回 2階線形微分方程式(1) (2018. 11. 6)
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第6回 変数分離形の変形 (2018. 10. 30)
PDF
2018年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 第5回 微分方程式とは・変数分離形 (2018. 10. 23)
PDF
2016年度秋学期 画像情報処理 第13回 Radon変換と投影定理 (2017. 1. 12))
PDF
2016年度秋学期 応用数学(解析) 第2回 無限にも大小がある (2016. 10. 6)
PDF
2016年度秋学期 応用数学(解析) 第7回 2階線形微分方程式(1) (2016. 11. 17)
PDF
2016年度秋学期 応用数学(解析) 第4回 収束とは何か,ε-δ論法 (2016. 10. 20)
Similar to 2015年度秋学期 応用数学(解析) 第13回 孤立特異点と留数 (2015. 12. 17)
PDF
2022年度秋学期 応用数学(解析) 第13回 複素関数論ダイジェスト(2) 孤立特異点と留数 (2022. 12. 22)
PDF
PDF
PDF
PDF
PDF
PDF
ブラック ショールズの方程式の解法 フーリエ級数と熱伝導方程式一 1st Edition すずきたろう
PDF
PDF
2016年度秋学期 画像情報処理 第3回 フーリエ変換とサンプリング定理 (2016. 10. 13)
PDF
PPTX
PDF
PDF
PPTX
PDF
フーリエ解析〜「フーリエ級数」から「高速フーリエ変換」まで〜
PDF
PDF
2014年度秋学期 応用数学(解析) 第1回 イントロダクション (2014. 9. 25)
PPTX
PDF
PDF
ある反転授業の試み:正規分布のTaylor展開をとおして
More from Akira Asano
PDF
2022年度秋学期 統計学 第15回 分布についての仮説を検証するー仮説検定(2) (2023. 1. 17)
PDF
2022年度秋学期 応用数学(解析) 第15回 測度論ダイジェスト(2) ルベーグ積分 (2023. 1. 19)
PDF
2022年度秋学期 応用数学(解析) 第14回 測度論ダイジェスト(1) ルベーグ測度と完全加法性 (2023. 1. 12)
PDF
2022年度秋学期 統計学 第14回 分布についての仮説を検証するー仮説検定(1) (2023. 1. 10)
PDF
2022年度秋学期 統計学 第13回 不確かな測定の不確かさを測る - 不偏分散とt分布 (2022. 12. 20)
PDF
2022年度秋学期 応用数学(解析) 第12回 複素関数論ダイジェスト(1) 複素関数・正則関数 (2022. 12. 15)
PDF
2022年度秋学期 統計学 第12回 分布の平均を推測する - 区間推定 (2022. 12. 13)
PDF
2022年度秋学期 画像情報処理 第11回 逆投影法による再構成 (2022. 12. 9)
PDF
2022年度秋学期 応用数学(解析) 第11回 振動と微分方程式 (2022. 12. 8)
PDF
2022年度秋学期 統計学 第11回 分布の「型」を考える - 確率分布モデルと正規分布 (2022. 12. 6)
PDF
2022年度秋学期 画像情報処理 第10回 Radon変換と投影切断面定理 (2022. 12. 2)
PDF
2022年度秋学期 応用数学(解析) 第10回 生存時間分布と半減期 (2022. 12. 1)
PDF
2022年度秋学期 統計学 第10回 分布の推測とはー標本調査,度数分布と確率分布 (2022. 11. 29)
PDF
2022年度秋学期 統計学 第8回 問題に対する答案の書き方 (2022. 11. 15)
PDF
2022年度秋学期 画像情報処理 第9回 離散フーリエ変換と離散コサイン変換 (2022. 11. 25)
PDF
2022年度秋学期 統計学 第9回 確からしさを記述するー確率 (2022. 11. 22)
PDF
2022年度秋学期 画像情報処理 第8回 行列の直交変換と基底画像 (2022. 11. 18)
PDF
2022年度秋学期 応用数学(解析) 第8回 2階線形微分方程式(2) (2022. 11. 17)
PDF
2022年度秋学期 画像情報処理 第7回 主成分分析とKarhunen-Loève変換 (2022. 11. 11)
PDF
2022年度秋学期 応用数学(解析) 第7回 2階線形微分方程式(1) (2022. 11. 10)
2015年度秋学期 応用数学(解析) 第13回 孤立特異点と留数 (2015. 12. 17) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 2015年度秋学期
A.Asano,KansaiUniv.
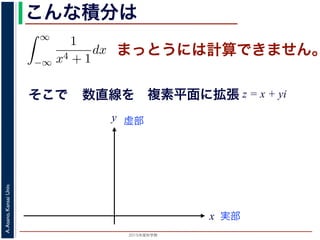
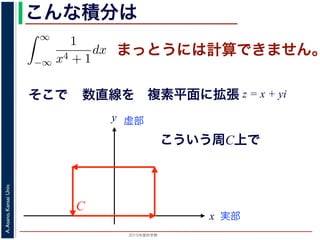
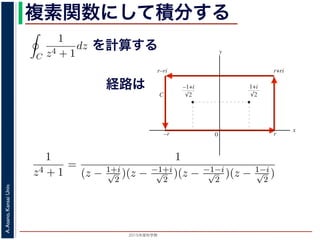
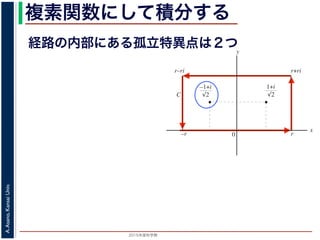
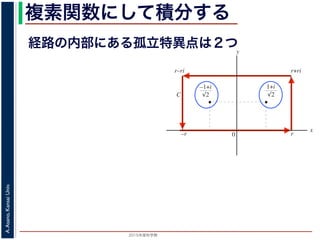
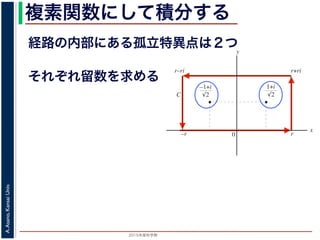
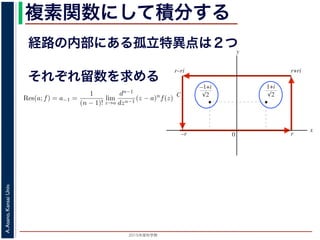
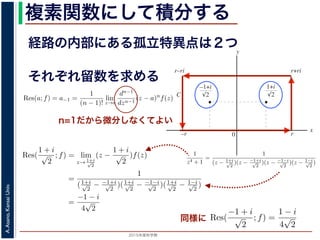
こんな積分は
まっとうには計算できません。
そこで
積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の
1
z4 + 1
の積分が,実軸上以外では r → 0 のとき 0 になる
上では |z| r であることを用います。
辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
r
0
1
r4 + 1
dy =
r
r4 + 1
∞
1 π
x
数直線を
実部
y 虚部
複素平面に拡張 z = x + yi
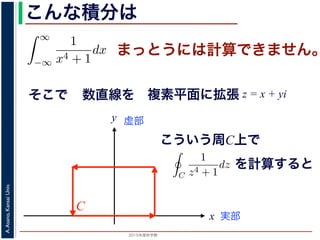
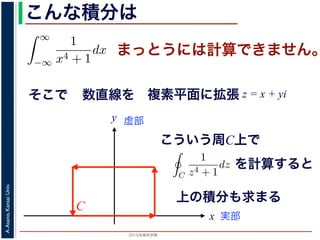
こういう周C上で
C
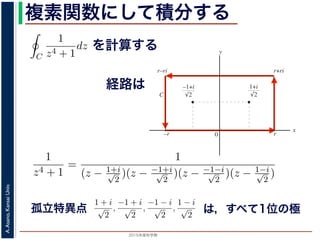
=
(1+i√
2
−
=
−1 −
4
√
2
となり,同様に Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となり
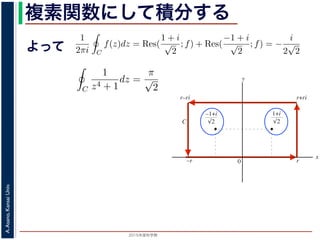
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1
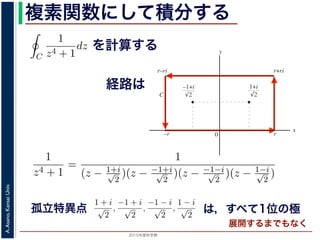
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます
浅野 晃/応用数学(解析)(2013 年度春学期) 第13回
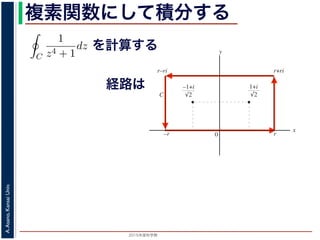
を計算すると
13. 2015年度秋学期
A.Asano,KansaiUniv.
こんな積分は
まっとうには計算できません。
そこで
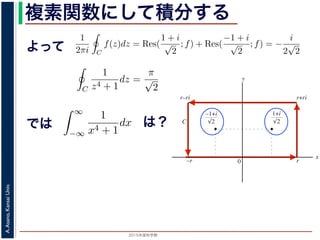
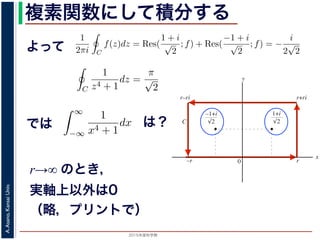
積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の
1
z4 + 1
の積分が,実軸上以外では r → 0 のとき 0 になる
上では |z| r であることを用います。
辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
r
0
1
r4 + 1
dy =
r
r4 + 1
∞
1 π
x
数直線を
実部
y 虚部
複素平面に拡張 z = x + yi
こういう周C上で
C
=
(1+i√
2
−
=
−1 −
4
√
2
となり,同様に Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となり
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます
浅野 晃/応用数学(解析)(2013 年度春学期) 第13回
を計算すると
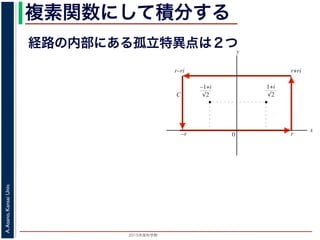
上の積分も求まる
14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = 0, 1, 2, … のとき
f(z) = z0, z1, z2, … は単位円周C の内部で正則
f(z) = zn の積分
今日の問題のような積分を考えるため
準備として,f(z) = zn を,単位円周(複
の向きにまわって積分した時の値を考え
C を単位円周とします。まず,n = 0,
分定理により
C
f(z)dz = 0 です。
一方,n = −1, −2, . . . のとき,あらた
f(z) は正則ではありません。この場合は
表されるので,
C
コーシーの積分定理により
32. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
33. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
考えるために,関数を級数で表して,各項に対する積分を考えます。その
単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
の値を考えます。
ず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
です。
とき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
= 1 のとき
1 2π
34. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
考えるために,関数を級数で表して,各項に対する積分を考えます。その
単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
の値を考えます。
ず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
です。
とき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
= 1 のとき
1 2π
実軸
虚軸
1
1
C
35. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
考えるために,関数を級数で表して,各項に対する積分を考えます。その
単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
の値を考えます。
ず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
です。
とき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
= 1 のとき
1 2π
経路 C 上で
実軸
虚軸
1
1
C
36. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
考えるために,関数を級数で表して,各項に対する積分を考えます。その
単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
の値を考えます。
ず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
です。
とき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
= 1 のとき
1 2π
経路 C 上で
るために,関数を級数で表して,各項に対する積分を考えま
周(複素平面における,原点を中心とする半径 1 の円周)に
を考えます。
= 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コー
。
あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき
場合は,単位円周 C を正の向きにまわる z が z = eiθ (0
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
e−inθ
ieiθ
dθ
ない点、いわば「穴」があいている場合はどうなるか,が今回の話題です。
分を考えるために,関数を級数で表して,各項に対する積分を考えます。その
,単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
た時の値を考えます。
。まず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
= 0 です。
のとき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
ん。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ (1)
実軸
虚軸
1
1
C
37. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
考えるために,関数を級数で表して,各項に対する積分を考えます。その
単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
の値を考えます。
ず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
です。
とき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
= 1 のとき
1 2π
経路 C 上で
るために,関数を級数で表して,各項に対する積分を考えま
周(複素平面における,原点を中心とする半径 1 の円周)に
を考えます。
= 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コー
。
あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき
場合は,単位円周 C を正の向きにまわる z が z = eiθ (0
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
e−inθ
ieiθ
dθ
ない点、いわば「穴」があいている場合はどうなるか,が今回の話題です。
分を考えるために,関数を級数で表して,各項に対する積分を考えます。その
,単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
た時の値を考えます。
。まず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
= 0 です。
のとき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
ん。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ (1)
実軸
虚軸
1
1
C
置換積分
38. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
n = –1, –2, –3, … のとき
ややこしいので,あらためて
えます。
, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシ
ためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ <
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
2π
とおいて n = 1, 2, 3, …とする
考えるために,関数を級数で表して,各項に対する積分を考えます。その
単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
の値を考えます。
ず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
です。
とき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
= 1 のとき
1 2π
経路 C 上で
るために,関数を級数で表して,各項に対する積分を考えま
周(複素平面における,原点を中心とする半径 1 の円周)に
を考えます。
= 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コー
。
あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき
場合は,単位円周 C を正の向きにまわる z が z = eiθ (0
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
e−inθ
ieiθ
dθ
ない点、いわば「穴」があいている場合はどうなるか,が今回の話題です。
分を考えるために,関数を級数で表して,各項に対する積分を考えます。その
,単位円周(複素平面における,原点を中心とする半径 1 の円周)にそって正
た時の値を考えます。
。まず,n = 0, 1, 2, . . . の場合は,円周内で zn は正則ですから,コーシーの積
= 0 です。
のとき,あらためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0 で
ん。この場合は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π) と
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ (1)
実軸
虚軸
1
1
C
置換積分
39. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
40. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
n = 1
41. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
n = 1
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
する半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
42. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
n = 1
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
する半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
n = 2, 3, … のとき
43. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
n = 1
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
する半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
n = 2, 3, … のとき
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(
分は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (
のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
(
2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
とする半径 1 の円周を C とするとき,
44. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
n = 1
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
する半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
n = 2, 3, … のとき
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(
分は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (
のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
(
2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
とする半径 1 の円周を C とするとき,
f(z) は正則ではありません。この場合は,単位円周 C を正の向きにまわる z が z
表されるので,
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
となります。この積分は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi
となり,n = 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
で,e2(1−n)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 ですより
45. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
について n = 1のときためて f(z) =
1
zn
(n = 1, 2, . . . ) とおきます。このとき,z = 0
は,単位円周 C を正の向きにまわる z が z = eiθ (0 θ < 2π)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
き
1 2π
=
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
る半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
きは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
n = 1
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(1)
は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (2)
ときは
C
1
zn
dz = i e2(n−1)πi
− 1 (3)
− 1)π) + i sin(2(n − 1)π) = 1 ですから上の積分は 0 です。
する半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
(4)
n = 2, 3, … のとき
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
(
分は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi (
のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
(
2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
とする半径 1 の円周を C とするとき,
f(z) は正則ではありません。この場合は,単位円周 C を正の向きにまわる z が z
表されるので,
C
f(z)dz =
2π
0
e−inθ dz
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
となります。この積分は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi
となり,n = 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
で,e2(1−n)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 ですより
一方,n = −1, −2, . . . のとき,あらためて f(z
f(z) は正則ではありません。この場合は,単位円
表されるので,
C
f(z)dz =
=
=
となります。この積分は,n = 1 のとき
C
1
z
dz =
となり,n = 2, 3, . . . のときは
C
1
zn
dz =
i(
C
f(z)dz =
0
e−inθ
dθ
dθ
=
2π
0
e−inθ
ieiθ
dθ
= i
2π
0
ei(1−n)θ
dθ
ます。この積分は,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi
,n = 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
1−n)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 で
46. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
つまり
C
1
z
dz = i
2π
0
dθ = 2πi
= 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の
a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3,
1 − n
)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分
,a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
す。
用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
= i
2π
0
ei(1−n)θ
dθ
のとき
C
1
z
dz = i
2π
0
dθ = 2πi
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
= i
0
ei(1−n)θ
dθ
= i
2π
0
dθ = 2πi
i
i(1 − n)
ei(1−n)θ
2π
0
1
1 − n
e2(1−n)πi
− 1
)π) = 1 ですから上の積分は 0 です。
47. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
つまり
C
1
z
dz = i
2π
0
dθ = 2πi
= 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の
a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3,
1 − n
)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分
,a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
す。
用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
= i
2π
0
ei(1−n)θ
dθ
のとき
C
1
z
dz = i
2π
0
dθ = 2πi
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
= i
0
ei(1−n)θ
dθ
= i
2π
0
dθ = 2πi
i
i(1 − n)
ei(1−n)θ
2π
0
1
1 − n
e2(1−n)πi
− 1
)π) = 1 ですから上の積分は 0 です。
また,a を中心とする半径1の円周を
C とすると
48. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
つまり
C
1
z
dz = i
2π
0
dθ = 2πi
= 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の
a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3,
1 − n
)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分
,a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
す。
用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
= i
2π
0
ei(1−n)θ
dθ
のとき
C
1
z
dz = i
2π
0
dθ = 2πi
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
= i
0
ei(1−n)θ
dθ
= i
2π
0
dθ = 2πi
i
i(1 − n)
ei(1−n)θ
2π
0
1
1 − n
e2(1−n)πi
− 1
)π) = 1 ですから上の積分は 0 です。
また,a を中心とする半径1の円周を
C とすると
実軸
虚軸
C
a
49. 2015年度秋学期
A.Asano,KansaiUniv.
zn の積分を考える
つまり
C
1
z
dz = i
2π
0
dθ = 2πi
= 2, 3, . . . のときは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の
a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3,
1 − n
)πi = cos(2(1 − n)π) + i sin(2(1 − n)π) = 1 ですから上の積分
,a を中心とする半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . .
す。
用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
= i
2π
0
ei(1−n)θ
dθ
のとき
C
1
z
dz = i
2π
0
dθ = 2πi
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
= i
0
ei(1−n)θ
dθ
= i
2π
0
dθ = 2πi
i
i(1 − n)
ei(1−n)θ
2π
0
1
1 − n
e2(1−n)πi
− 1
)π) = 1 ですから上の積分は 0 です。
また,a を中心とする半径1の円周を
C とすると
= i
0
e dθ
,n = 1 のとき
C
1
z
dz = i
2π
0
dθ = 2πi
きは
C
1
zn
dz =
i
i(1 − n)
ei(1−n)θ
2π
0
=
1
1 − n
e2(1−n)πi
− 1
n)π) + i sin(2(1 − n)π) = 1 ですから上の積分は 0 です。
半径 1 の円周を C とするとき,
C
1
(z − a)n
dz =
2πi n = 1
0 n = 2, 3, . . . 実軸
虚軸
C
a
50. 51. 52. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
正則関数の任意の点での値は,
その点を囲む閉曲線上の値だけできまる
領域 D で正則な関数fの点 z における値 f(z) は,
D 内で点 z を囲み,正の方向に1周する閉曲線 C 上の積分
図 1: コーシーの積分公式
,領域 D で正則な関数 f の点 z における値 f(z) が,D 内で点 z を囲み
に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
す。とくに z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線と
f(0) =
1
2πi C
f(ζ)
ζ
dζ
,正則関数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってし
関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたよ
での関数の値が周囲での値によって決まってしまう,というのは,それ
で表される
z = 0 のときは
原点を囲み,正の方向に1周する閉曲線 C 上の積分
P
図 1: コーシーの積分公式
,領域 D で正則な関数 f の点 z における値 f(z) が,D 内で点 z を囲み
沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
す。とくに z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線と
f(0) =
1
2πi C
f(ζ)
ζ
dζ
,正則関数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってし
で表される
53. 54. 55. 56. 57. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
58. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
59. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
60. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
61. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
62. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
63. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
64. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
65. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
66. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
67. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
68. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
69. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
70. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
原点では正則でないが
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
71. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
原点では正則でないが
グレーの部分では正則
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
72. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
f(z) =
2πi C ζ − z
dζ (5)
に z = 0 のとき,C を原点を囲み正の方向に一周する閉曲線として
f(0) =
1
2πi C
f(ζ)
ζ
dζ (6)
数 f の点 z での値は,z を囲む閉曲線上の値だけで決まってしまうこ
軟らかい板を,ぐにゃぐにゃとどこにも折り目がなく曲げたようなも
の値が周囲での値によって決まってしまう,というのは,それほど不
1 のような,原点を囲む閉曲線 C とその内側で原点を囲む半径 r の円
を考えます。関数
f(ζ)
ζ
は原点で正則ではありませんが,P から C を正
きに1周→ QP という経路を考えると,この経路は閉曲線で,その内
て,コーシーの積分定理により
Q
f(ζ) f(ζ) P
f(ζ)
を考える
O
C
Cr
P
Q
図 1: コーシーの積分公式
原点
こういう経路で
原点では正則でないが
グレーの部分では正則
を積分
シーの積分公式は,領域 D で正則な関数 f の点 z における値 f(z) が,
周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
れるというものです。とくに z = 0 のとき,C を原点を囲み正の方向に
f(0) =
1
2πi C
f(ζ)
ζ
dζ
ます。この公式は,正則関数 f の点 z での値は,z を囲む閉曲線上の値
しています。正則関数を「軟らかい板を,ぐにゃぐにゃとどこにも折り
考えれば,ある点での関数の値が周囲での値によって決まってしまう,
はありません。
式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C とその内側
れに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正則ではあり
に1周→ PQ → C を逆向きに1周→ QP という経路を考えると,この
関数
コーシーの積分定理により,
積分=0
73. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
74. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
75. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
76. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
77. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
同じ経路を逆方向だから
打ち消し合う
78. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
同じ経路を逆方向だから
打ち消し合う
79. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
同じ経路を逆方向だから
打ち消し合う
80. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
C とは逆回りだからマイナス
同じ経路を逆方向だから
打ち消し合う
81. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
C とは逆回りだからマイナス
同じ経路を逆方向だから
打ち消し合う
の向きに1周→ PQ → Cr を逆向きに1周→ QP という経路を考えると
部で関数
f(ζ)
ζ
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
−Cr
f(ζ)
ζ
dζ = −
Cr
f(ζ)
ζ
dζ
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) htt
82. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
グレーの部分では正則 コーシーの積分定理により,
両者を結ぶ線分 PQ を考えます。関数
ζ
は原点で正則ではありませんが,P か
周→ PQ → Cr を逆向きに1周→ QP という経路を考えると,この経路は閉曲線
ζ)
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f(ζ)
ζ
dζ = 0
の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は
に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
するのかは,参考文献を参照してください。
数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp
C とは逆回りだからマイナス
同じ経路を逆方向だから
打ち消し合う
の向きに1周→ PQ → Cr を逆向きに1周→ QP という経路を考えると
部で関数
f(ζ)
ζ
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
P
Q
f
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
−Cr
f(ζ)
ζ
dζ = −
Cr
f(ζ)
ζ
dζ
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) htt
つまり
の」と考えれば,ある点での関数の値が周囲での値によって決まっ
思議ではありません。
(6) 式の意味を考えるため,図 1 のような,原点を囲む閉曲線 C
Cr,それに両者を結ぶ線分 PQ を考えます。関数
f(ζ)
ζ
は原点で正
の向きに1周→ PQ → Cr を逆向きに1周→ QP という経路を考え
部で関数
f(ζ)
ζ
は正則です。よって,コーシーの積分定理により
C
f(ζ)
ζ
dζ +
Q
P
f(ζ)
ζ
dζ +
−Cr
f(ζ)
ζ
dζ +
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
f(0)
dζ に収束し 1,
83. 84. 85. 86. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
内側の円の半径→0とすると
積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は (−1) × C
ので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ (8
式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分を使うと
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0) (9
照してください。
学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 2/7 ページ
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://r
に収束する
(詳細略)
87. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
内側の円の半径→0とすると
積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は (−1) × C
ので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ (8
式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分を使うと
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0) (9
照してください。
学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 2/7 ページ
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://r
に収束する
(詳細略)
C ζ P ζ −Cr
ζ Q
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
88. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
内側の円の半径→0とすると
積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は (−1) × C
ので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ (8
式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分を使うと
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0) (9
照してください。
学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 2/7 ページ
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://r
に収束する
(詳細略)
C ζ P ζ −Cr
ζ Q
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
89. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
内側の円の半径→0とすると
積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は (−1) × C
ので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ (8
式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分を使うと
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0) (9
照してください。
学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 2/7 ページ
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://r
に収束する
(詳細略)
C ζ P ζ −Cr
ζ Q
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
90. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
内側の円の半径→0とすると
積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は (−1) × C
ので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ (8
式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分を使うと
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0) (9
照してください。
学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 2/7 ページ
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://r
に収束する
(詳細略)
C ζ P ζ −Cr
ζ Q
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
よって
91. 2015年度秋学期
A.Asano,KansaiUniv.
コーシーの積分公式
O
C
Cr
P
Q
内側の円の半径→0とすると
積分は打ち消し合い,−Cr(Cr の負の方向)に沿った積分は (−1) × C
ので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ (8
式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明した
1
z
の積分を使うと
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0) (9
照してください。
学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 2/7 ページ
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方向)に
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節で説明
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://r
に収束する
(詳細略)
C ζ P ζ −Cr
ζ Q
で,P → Q の積分と Q → P の積分は打ち消し合い,−Cr(Cr の負の方
の正の方向に沿った積分 となるので,
C
f(ζ)
ζ
dζ =
Cr
f(ζ)
ζ
dζ
となります。r → 0 のとき,上式の右辺は
Cr
f(0)
ζ
dζ に収束し 1,前節
Cr
f(0)
ζ
dζ = f(0)
Cr
1
ζ
dζ = 2πif(0)
1
なぜ収束するのかは,参考文献を参照してください。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) ht
よって
P
図 1: コーシーの積分公式
コーシーの積分公式
コーシーの積分公式は,領域 D で正則な関数 f の点 z における
向に1周する閉曲線 C に沿った積分を使って
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ
と表されるというものです。とくに z = 0 のとき,C を原点を囲
f(0) =
1
2πi C
f(ζ)
ζ
dζ
となります。この公式は,正則関数 f の点 z での値は,z を囲む
とを示しています。正則関数を「軟らかい板を,ぐにゃぐにゃと
92. 93. 94. 95. 96. 97. 98. 99. 100. 101. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
102. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
103. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
等比級数の形
f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
104. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
等比級数の形
f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
105. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
等比級数の形
f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
ζ は外側の経路上だから
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
106. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
等比級数の形
f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
ζ は外側の経路上だから
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
絶対値が1より小さく,収束する
107. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
等比級数の形
f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
。
(10) 式の第1項の積分の過程では,ζ が外側の経路 C を動き,z は C
− a| です。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
と,右辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
。同様に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き
ζ は外側の経路上だから
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
絶対値が1より小さく,収束する
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ (10
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にあるので
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
(11
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · · (12
,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き,z は C′ の外部に
108. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
す。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
(1
辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · · (1
に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き,z は C′ の外部
を参照してください。
)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 3/7 ペー
109. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
す。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
(1
辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · · (1
に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き,z は C′ の外部
を参照してください。
)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 3/7 ペー
110. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
こちらの ζ は内側の経路上
す。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
(1
辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · · (1
に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き,z は C′ の外部
を参照してください。
)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 3/7 ペー
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
111. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開f(z) は正則ですから,f(z) をコーシーの積分公式を用いて表すことができま
考慮すると
f(z) =
1
2πi C
f(ζ)
ζ − z
dζ −
1
2πi C′
f(ζ)
ζ − z
dζ
第1項の積分の過程では,ζ が外側の経路 C を動き,z は C の内部にある
。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · ·
こちらの ζ は内側の経路上
す。そこで,
1
ζ − z
=
1
(ζ − a) − (z − a)
=
1
ζ − a
·
1
1 −
z − a
ζ − a
(1
辺の 2 つめの分数は初項 1,公比
z − a
ζ − a
の等比級数の和で表され,
1
ζ − z
=
1
ζ − a
1 +
z − a
ζ − a
+
z − a
ζ − a
2
+ · · · (1
に,(10) 式の第2項の積分の過程では,ζ が内側の経路 C′ を動き,z は C′ の外部
を参照してください。
)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 3/7 ペー
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
あるので |ζ − a| < |z − a| で,
1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
と表されます。
(12) 式,(13) 式を (11) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z −
112. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
以上から
1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
ζ − z
=
ζ − a
1 +
z − a
+
z − a
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
113. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開
以上から
1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
ζ − z
=
ζ − a
1 +
z − a
+
z − a
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
孤立特異点 a のまわりのローラン級数
114. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開れます。
式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ます 3。
で,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
ことができます。
f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
いいます。
されます。
) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
すことができます。
数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
といいます。
数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の極といいます。これは,
115. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開れます。
式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ます 3。
で,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
ことができます。
f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
いいます。
されます。
) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
すことができます。
数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
といいます。
数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の極といいます。これは,
ところで
116. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開れます。
式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ます 3。
で,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
ことができます。
f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
いいます。
されます。
) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
すことができます。
数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
といいます。
数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の極といいます。これは,
ところで
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経路も含めて)平行移動すると,(5)
式が得られます 2。
117. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開れます。
式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ます 3。
で,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
ことができます。
f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
いいます。
されます。
) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
すことができます。
数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
といいます。
数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の極といいます。これは,
ところで
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経路も含めて)平行移動すると,(5)
式が得られます 2。
と表されます。
(12) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
ただし
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
となります 3。
ここで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
であり,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . )
と表すことができます。
関数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのロー
118. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開れます。
式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ます 3。
で,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
ことができます。
f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
いいます。
されます。
) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
すことができます。
数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
といいます。
数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の極といいます。これは,
ところで
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経路も含めて)平行移動すると,(5)
式が得られます 2。
グレーの部分で f(z) は正則なので,
コーシーの積分定理より
と表されます。
(12) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
ただし
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
となります 3。
ここで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
であり,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . )
と表すことができます。
関数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのロー
119. 2015年度秋学期
A.Asano,KansaiUniv.
ローラン級数展開れます。
式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ます 3。
で,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
ことができます。
f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
いいます。
されます。
) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
(14)
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . ) (15)
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . ) (16)
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0 (17)
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . ) (18)
すことができます。
数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのローラン (Laurent) 級数
といいます。
数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の極といいます。これは,
ところで
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経路も含めて)平行移動すると,(5)
式が得られます 2。
グレーの部分で f(z) は正則なので,
コーシーの積分定理より
と表されます。
(12) 式,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
ただし
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
となります 3。
ここで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
であり,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . )
と表すことができます。
関数 f(z) をこのような級数で表すことを,f(z) の孤立特異点 a のまわりのロー
よって
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ ·
し
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
ります 3。
こで,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi C
f(ζ)(ζ − a)n−1
dζ −
1
2πi C′
f(ζ)(ζ − a)n−1
dζ = 0
り,これを使うと,(15) 式と (16) 式を合わせて
an =
1
2πi C
f(ζ)(ζ − a)−n−1
dζ (n = 0, ±1, ±2, . . . )
120. 121. 122. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
123. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
124. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
125. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
つまり
126. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
127. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
f(z) の孤立特異点 a における
[留数 (residue)]という
128. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
f(z) の孤立特異点 a における
[留数 (residue)]という
,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表します。
n 位の極であるとき
z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · · (20)
129. 2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
f(z) の孤立特異点 a における
[留数 (residue)]という
,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表します。
n 位の極であるとき
z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · · (20)
留数を別の方法で求められれば,積分は簡単に計算できる
130. 131. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
132. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
両辺を (n – 1) 回微分すると
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
133. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
両辺を (n – 1) 回微分すると
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
134. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
両辺を (n – 1) 回微分すると
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
微分によって,a-1 の手前の項まで消える
135. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
136. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
137. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
138. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
よって
139. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
よって
− a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) +
数が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
n−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留
式が計算できれば求められることを表しています。
C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則
. . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路
でと同様の考えで,コーシーの積分定理により
140. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
よって
− a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) +
数が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
n−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留
式が計算できれば求められることを表しています。
C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則
. . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路
でと同様の考えで,コーシーの積分定理により
孤立特異点を囲んだ閉曲線上の積分は
留数で表される
141. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
よって
− a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) +
数が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
n−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留
式が計算できれば求められることを表しています。
C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則
. . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路
でと同様の考えで,コーシーの積分定理により
孤立特異点を囲んだ閉曲線上の積分は
留数で表される
関数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の
ローラン級数の負のべきの項が有限,すなわち級数が a−n (n 1) から始まるこ
略)。このとき,a を n 位の極といいます。なお,負のべきの項が無限に現れると
とよばれます。
留数
図 2 において,f(z) を円環部分の中にある円周 C′′ に沿って正の向きに1周し
ます。f(z) をローラン級数展開したものの各項を積分すると考えると,今回の最
分」により,
1
z − a
の項以外はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
3
本当は,ここで「無限級数の積分」を「積分の無限級数」に置き換えられるのは,当然ではあ
は略します。
142. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
よって
− a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) +
数が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
n−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留
式が計算できれば求められることを表しています。
C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則
. . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路
でと同様の考えで,コーシーの積分定理により
孤立特異点を囲んだ閉曲線上の積分は
留数で表される
関数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の
ローラン級数の負のべきの項が有限,すなわち級数が a−n (n 1) から始まるこ
略)。このとき,a を n 位の極といいます。なお,負のべきの項が無限に現れると
とよばれます。
留数
図 2 において,f(z) を円環部分の中にある円周 C′′ に沿って正の向きに1周し
ます。f(z) をローラン級数展開したものの各項を積分すると考えると,今回の最
分」により,
1
z − a
の項以外はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
3
本当は,ここで「無限級数の積分」を「積分の無限級数」に置き換えられるのは,当然ではあ
は略します。
n位の極については,留数は別途求まる
143. 2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
(z − a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) + · · ·
,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
れます。これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で
数は上の式が計算できれば求められることを表しています。
,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則である
き,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C
,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ら,
z→a のとき,これらの項は0
よって
− a) f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a) + a0(z − a) +
数が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
n−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
これらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留
式が計算できれば求められることを表しています。
C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則
. . . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路
でと同様の考えで,コーシーの積分定理により
孤立特異点を囲んだ閉曲線上の積分は
留数で表される
関数 f(z) と孤立特異点 a について,|f(z)| → ∞ (z → a) のとき,a を f(z) の
ローラン級数の負のべきの項が有限,すなわち級数が a−n (n 1) から始まるこ
略)。このとき,a を n 位の極といいます。なお,負のべきの項が無限に現れると
とよばれます。
留数
図 2 において,f(z) を円環部分の中にある円周 C′′ に沿って正の向きに1周し
ます。f(z) をローラン級数展開したものの各項を積分すると考えると,今回の最
分」により,
1
z − a
の項以外はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
3
本当は,ここで「無限級数の積分」を「積分の無限級数」に置き換えられるのは,当然ではあ
は略します。
n位の極については,留数は別途求まる
144. 145. 146. 2015年度秋学期
A.Asano,KansaiUniv.
孤立特異点がいくつあっても
b1
C
C1
b2
C2
b3
C3
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
このとき,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周
すると,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ですから,
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
がなりたちます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,
数がわかれば求められることを示しています。
留数と定積分
留数の考えを使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った
考えます。
1
z4 + 1
=
1
(z − 1+i√ )(z − −1+i√ )(z − −1−i√ )(z − 1−i√ )
1 2
すると,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ですから,
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
がなりたちます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,そ
数がわかれば求められることを示しています。
留数と定積分
留数の考えを使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った
考えます。
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
147. 148. 149. 150. 151. 152. 2015年度秋学期
A.Asano,KansaiUniv.
こんな積分は
まっとうには計算できません。
そこで
積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の
1
z4 + 1
の積分が,実軸上以外では r → 0 のとき 0 になる
上では |z| r であることを用います。
辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
r
0
1
r4 + 1
dy =
r
r4 + 1
∞
1 π
x
数直線を
実部
y 虚部
複素平面に拡張 z = x + yi
こういう周C上で
C
=
(1+i√
2
−
=
−1 −
4
√
2
となり,同様に Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となり
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます
浅野 晃/応用数学(解析)(2013 年度春学期) 第13回
を計算すると
153. 2015年度秋学期
A.Asano,KansaiUniv.
こんな積分は
まっとうには計算できません。
そこで
積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の
1
z4 + 1
の積分が,実軸上以外では r → 0 のとき 0 になる
上では |z| r であることを用います。
辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
r
0
1
r4 + 1
dy =
r
r4 + 1
∞
1 π
x
数直線を
実部
y 虚部
複素平面に拡張 z = x + yi
こういう周C上で
C
=
(1+i√
2
−
=
−1 −
4
√
2
となり,同様に Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となり
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます
浅野 晃/応用数学(解析)(2013 年度春学期) 第13回
を計算すると
上の積分も求まる
154. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
なわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
/応用数学(解析)(2013 年度春学期) 第13回 (2013. 7. 9) http://
を計算する
経路は
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式よ
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
155. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
なわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
/応用数学(解析)(2013 年度春学期) 第13回 (2013. 7. 9) http://
を計算する
経路は
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式よ
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれ
られることを示しています。
って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った f(z) =
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて1位の極
156. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
なわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
/応用数学(解析)(2013 年度春学期) 第13回 (2013. 7. 9) http://
を計算する
経路は
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式よ
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれ
られることを示しています。
って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った f(z) =
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて1位の極
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25
ます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
ば求められることを示しています。
分
を使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った f(z) =
1
z4 + 1
の積分を
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
(26
つある f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて1位の極です。孤立特異点 は,すべて1位の極
157. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
なわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
/応用数学(解析)(2013 年度春学期) 第13回 (2013. 7. 9) http://
を計算する
経路は
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式よ
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれ
られることを示しています。
って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った f(z) =
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて1位の極
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25
ます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
ば求められることを示しています。
分
を使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った f(z) =
1
z4 + 1
の積分を
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
(26
つある f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて1位の極です。孤立特異点 は,すべて1位の極
展開するまでもなく
158. 159. 160. 161. 162. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
163. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
164. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
n=1だから微分しなくてよい
165. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
n=1だから微分しなくてよい
0 r
x
√2 √2
–r
C
図 4: 留数と定積分
の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式より
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
=
1
(1+i√
2
− −1+i√
2
)(1+i√
2
− −1−i√
2
)(1+i√
2
− 1−i√
2
)
=
−1 − i
4
√
2
(27)
Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となります。
166. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
n=1だから微分しなくてよい
また,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除い
このとき,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周す
すると,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ですから,
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
がなりたちます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,
数がわかれば求められることを示しています。
留数と定積分
留数の考えを使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った
考えます。
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
ですから,4 つある f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて
4
こう言えるのは,ローラン級数が「一様収束」しているからです。詳細は略します。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://rac
0 r
x
√2 √2
–r
C
図 4: 留数と定積分
の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式より
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
=
1
(1+i√
2
− −1+i√
2
)(1+i√
2
− −1−i√
2
)(1+i√
2
− 1−i√
2
)
=
−1 − i
4
√
2
(27)
Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となります。
167. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
n=1だから微分しなくてよい
また,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除い
このとき,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周す
すると,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ですから,
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
がなりたちます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,
数がわかれば求められることを示しています。
留数と定積分
留数の考えを使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った
考えます。
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
ですから,4 つある f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて
4
こう言えるのは,ローラン級数が「一様収束」しているからです。詳細は略します。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://rac
0 r
x
√2 √2
–r
C
図 4: 留数と定積分
の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式より
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
=
1
(1+i√
2
− −1+i√
2
)(1+i√
2
− −1−i√
2
)(1+i√
2
− 1−i√
2
)
=
−1 − i
4
√
2
(27)
Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となります。
168. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
経路の内部にある孤立特異点は2つ
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(2
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
それぞれ留数を求める
,
a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · · (21)
が得られます。したがって,両辺を (n − 1) 回微分すると,
−1
−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · · (22)
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z) (23)
れらのことは,孤立特異点つまり「穴」を囲んだ閉曲線上の積分が,留数で表され,し
が計算できれば求められることを表しています。
の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除いて正則であるとします。
. . のそれぞれを囲み C の内部にある円周を正の向きに一周する経路を C1, C2, . . . と
と同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0 (24)
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · · (25)
このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,それぞれの「穴」での留
n=1だから微分しなくてよい
また,閉曲線 C の内部で,関数 f(z) が有限個の孤立特異点 b1, b2, . . . を除い
このとき,b1, b2, . . . のそれぞれを囲み C の内部にある円周を正の向きに一周す
すると,これまでと同様の考えで,コーシーの積分定理により
C
f(z)dz −
C1
f(z)dz −
C2
f(z)dz − · · · = 0
ですから,
1
2πi C
f(z)dz = Res(b1; f) + Res(b2; f) + · · ·
がなりたちます。このことは,いくつかの「穴」を囲んだ閉曲線上の積分は,
数がわかれば求められることを示しています。
留数と定積分
留数の考えを使って,図 4 に示す,幅 2r・高さ r の長方形の経路 C に沿った
考えます。
1
z4 + 1
=
1
(z − 1+i√
2
)(z − −1+i√
2
)(z − −1−i√
2
)(z − 1−i√
2
)
ですから,4 つある f(z) の孤立特異点
1 + i
√
2
,
−1 + i
√
2
,
−1 − i
√
2
,
1 − i
√
2
は,すべて
4
こう言えるのは,ローラン級数が「一様収束」しているからです。詳細は略します。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://rac
–r
図 4
図 4 の経路 C の内部に入っている極は,
1 +
√
Res(
1 + i
√
2
; f) = lim
z→1+i√
2
(
=
(1+i√
2
−
=
−1 −
4
√
2
となり,同様に Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となり同様に
0 r
x
√2 √2
–r
C
図 4: 留数と定積分
の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,(23) 式より
Res(
1 + i
√
2
; f) = lim
z→ 1+i√
2
(z −
1 + i
√
2
)f(z)
=
1
(1+i√
2
− −1+i√
2
)(1+i√
2
− −1−i√
2
)(1+i√
2
− 1−i√
2
)
=
−1 − i
4
√
2
(27)
Res(
−1 + i
√
2
; f) =
1 − i
4
√
2
となります。
169. 170. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
よって
b2
C2
b3
C3
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,
2 4 2
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
i
2
√
2
,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.miken
2 4 2
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f)
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) h
では実関数の積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の辺での
1
z4 + 1
の積分が,実軸上以外では r → ∞ のとき 0 になるこ
外の辺上では |z| r であることを用います。
側の立辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
は?
171. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
よって
b2
C2
b3
C3
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,
2 4 2
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
i
2
√
2
,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.miken
2 4 2
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f)
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) h
では実関数の積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の辺での
1
z4 + 1
の積分が,実軸上以外では r → ∞ のとき 0 になるこ
外の辺上では |z| r であることを用います。
側の立辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
は?
r→∞ のとき,
実軸上以外は0
(略,プリントで)
172. 2015年度秋学期
A.Asano,KansaiUniv.
複素関数にして積分する
よって
b2
C2
b3
C3
図 3: 有限個の孤立特異点を含む場合
y
0
–1+i
r
x
√2
1+i
√2
–r
r+rir–ri
C
図 4: 留数と定積分
図 4 の経路 C の内部に入っている極は,
1 + i
√
2
,
−1 + i
√
2
だけです。ここで,
2 4 2
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f) = −
i
2
√
2
,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) http://racco.miken
2 4 2
よって,(25) 式より,
1
2πi C
f(z)dz = Res(
1 + i
√
2
; f) + Res(
−1 + i
√
2
; f)
で,すなわち
C
1
z4 + 1
dz =
π
√
2
が得られます。
浅野 晃/応用数学(解析)(2014 年度春学期) 第14回 (2015. 1. 8) h
では実関数の積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。そのために,
の辺での
1
z4 + 1
の積分が,実軸上以外では r → ∞ のとき 0 になるこ
外の辺上では |z| r であることを用います。
側の立辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
は?
r→∞ のとき,
実軸上以外は0
(略,プリントで)
を使って,実関数の積分
∞
−∞
1
x4 + 1
dx を求めることを考えます。
,それぞれの辺での
1
z4 + 1
の積分が,実軸上以外では r → ∞ のと
は,実軸以外の辺上では |z| r であることを用います。
長方形の右側の立辺では
r+ri
r
1
z4 + 1
dz
r+ri
r
1
|z|4 + 1
d|z|
r
0
1
r4 + 1
dy =
r
r4 + 1
のとき 0 になります。他の辺でも同様で,
∞
−∞
1
x4 + 1
dx =
π
√
2
がよって
173.







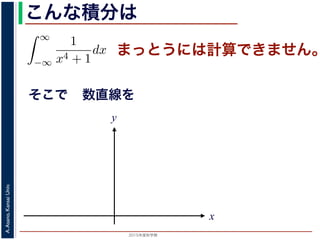
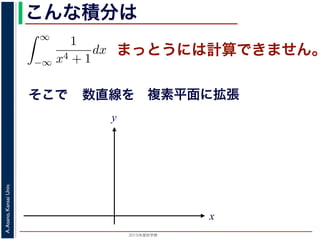
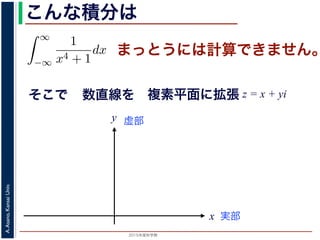
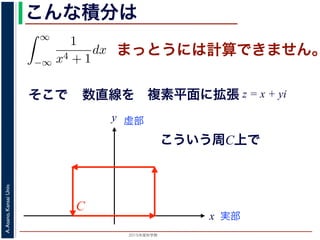
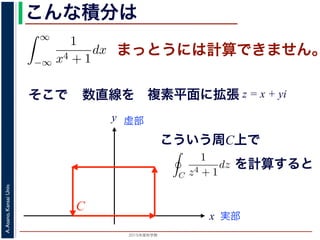



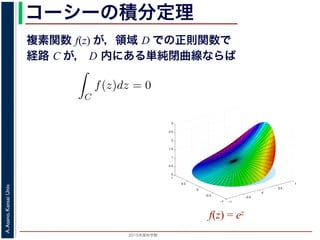
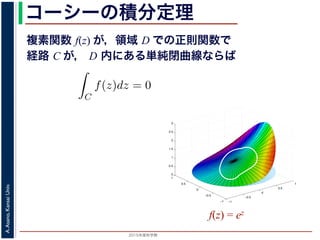


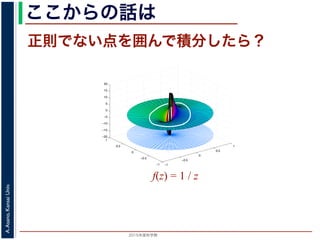
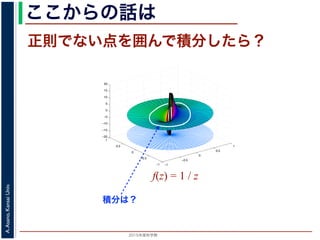






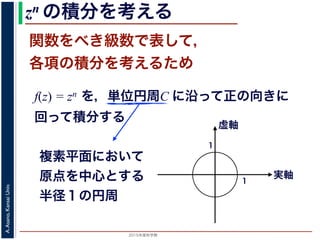
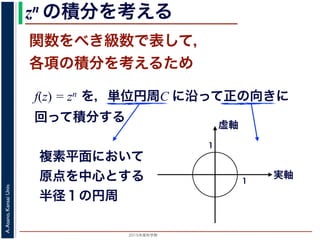
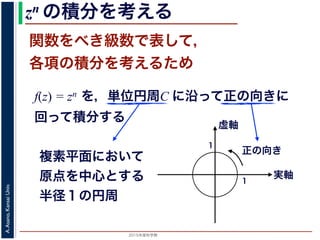







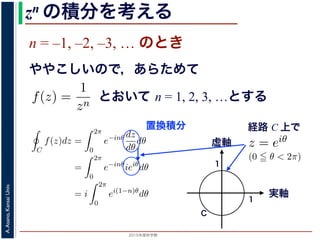














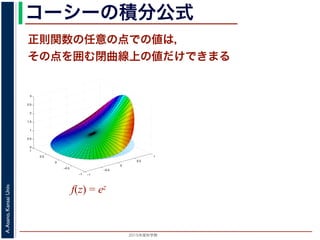

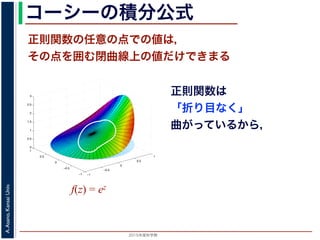
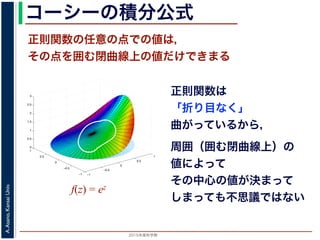
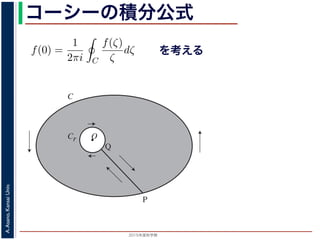
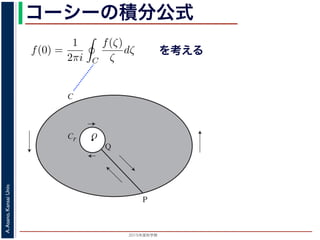
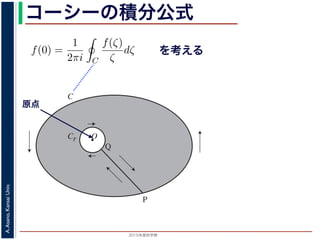
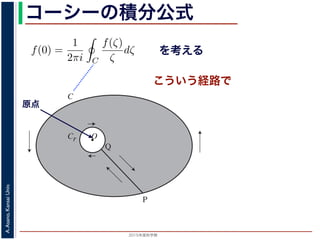

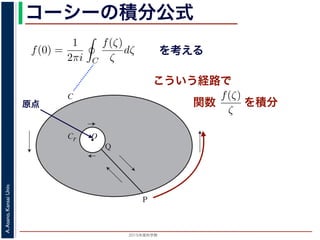
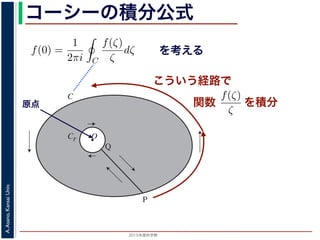
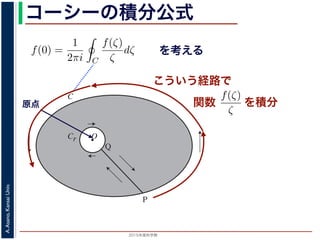
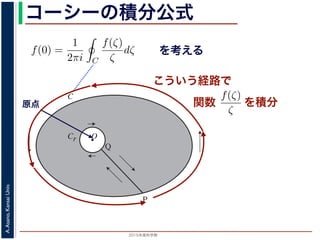
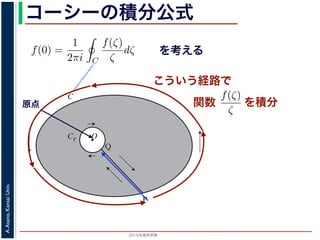
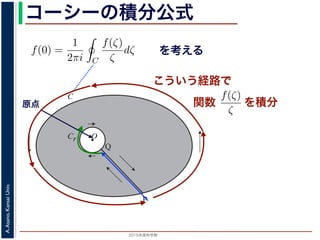

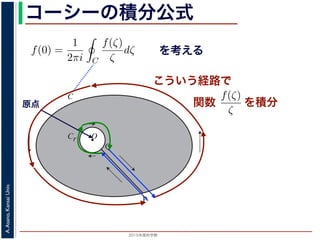
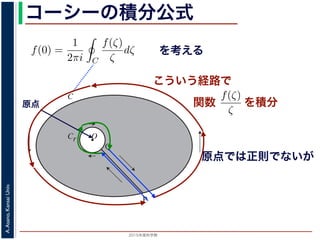

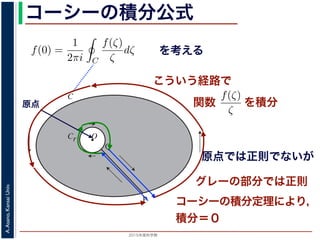

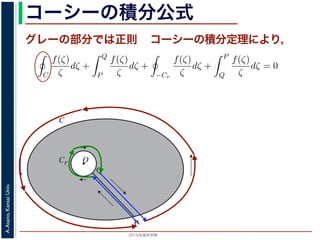
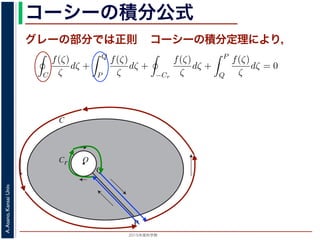
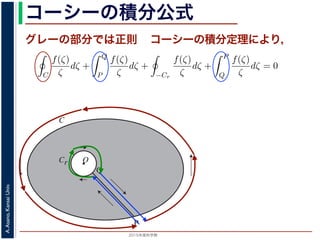

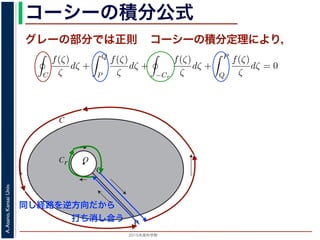
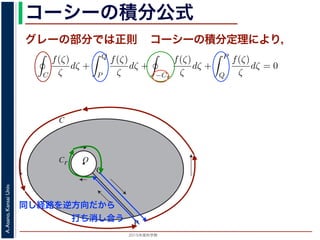

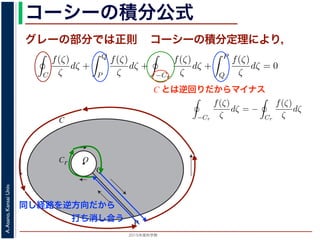
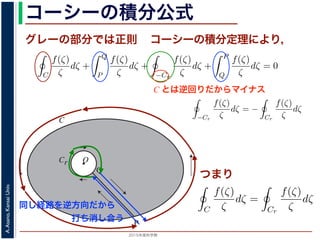

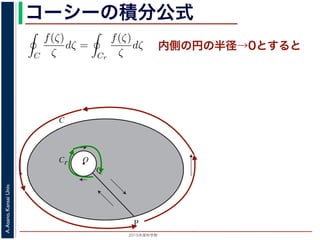
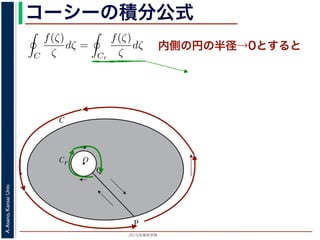
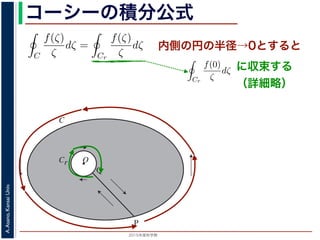


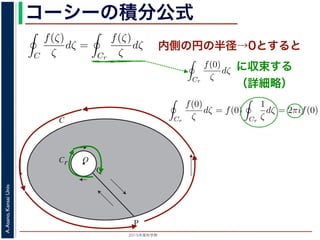
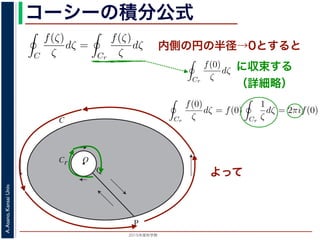
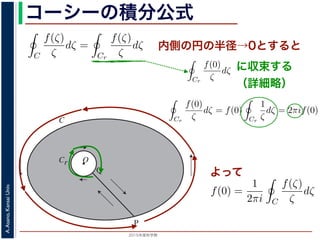


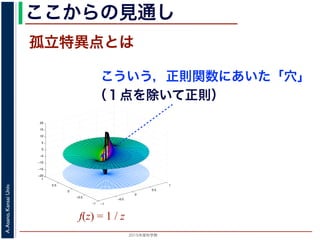

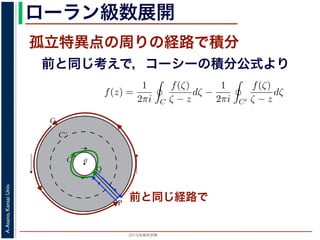
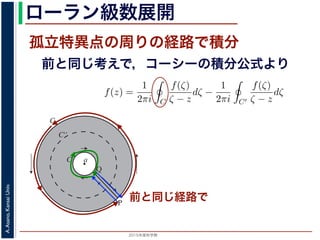
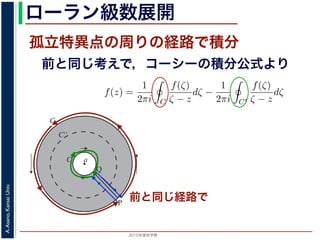




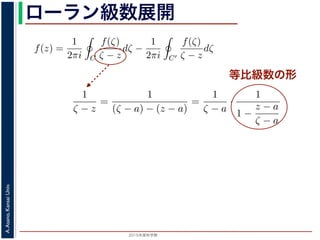
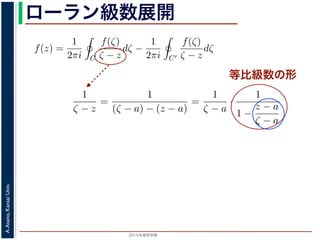
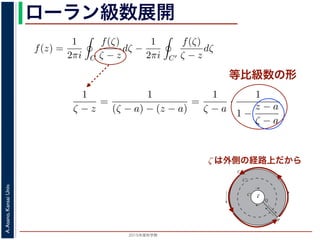


















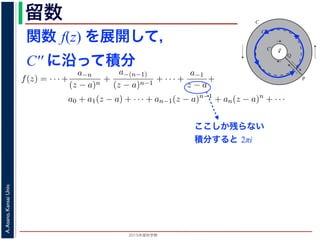


![2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
f(z) の孤立特異点 a における
[留数 (residue)]という](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-127-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
f(z) の孤立特異点 a における
[留数 (residue)]という
,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表します。
n 位の極であるとき
z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · · (20)](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-128-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
留数 1
ζ − z
=
−1
ζ − a
1 +
ζ − a
z − a
+
ζ − a
z − a
2
+ · · ·
ます。
,(13) 式を (10) 式に代入すると,
f(z) = · · · +
a−n
(z − a)n
+
a−(n−1)
(z − a)n−1
+ · · · +
a−1
z − a
+
a0 + a1(z − a) + · · · + an−1(z − a)n−1
+ an(z − a)n
+ · · ·
an =
1
2πi C
f(ζ)
(ζ − a)n+1
dζ (n = 0, 1, 2, . . . )
a−n =
1
2πi C′
f(ζ)(ζ − a)n−1
dζ (n = 1, 2, . . . )
す 3。
,図 2 の円環領域で f(z) は正則なので,コーシーの積分定理により
1
2πi
f(ζ)(ζ − a)n−1
dζ −
1
2πi ′
f(ζ)(ζ − a)n−1
dζ = 0
関数 f(z) を展開して,
C′′ に沿って積分
a
C
Cʹ
P
Q
Cʹʹ
図 2: 孤立特異点とローラン級数展開
となりますから,(6) 式が得られました。これをさらに z だけ(積分経
式が得られます 2。
孤立特異点とローラン級数展開
領域 D において,関数 f(z) が1点 a を除いて正則であるとき,a
つまり,今日の最初に述べた「穴」です。
このとき,a を中心とする円周 C と,その内部にありやはり a を中
ように,P から C を正の向きに1周→ PQ → C′ を逆向きに1周→ Q
すると,経路の内部で f(z) は正則ですから,f(z) をコーシーの積分公
図 1 と同様の関係を考慮すると
f(z) =
1
2πi
f(ζ)
ζ − z
dζ −
1
2πi ′
f(ζ
ζ −
ここしか残らない
積分すると 2πi
部分の中にある円周 C′′ に沿って正の向きに1周して積分することを考
開したものの各項を積分すると考えると,今回の最初に説明した「zn の
はすべて 0 となり,
a−1 =
1
2πi C′′
f(z)dz
分」を「積分の無限級数」に置き換えられるのは,当然ではありませんが,ここでは
度春学期) 第14回 (2015. 1. 8) http://racco.mikeneko.jp/ 4/7 ペ
つまり
f(z) の孤立特異点 a における
[留数 (residue)]という
,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表します。
n 位の極であるとき
z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · · (20)
留数を別の方法で求められれば,積分は簡単に計算できる](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-129-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-130-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-131-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
両辺を (n – 1) 回微分すると
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-132-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
両辺を (n – 1) 回微分すると
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-133-320.jpg)
![2015年度秋学期
A.Asano,KansaiUniv.
「n位の極」と留数
ローラン級数がa-nから始まるような
孤立特異点を,[n位の極]という
両辺を (n – 1) 回微分すると
の a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,
異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
,
)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z −
が得られます。したがって,両辺を (n − 1) 回微分すると,
1
1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z −
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
ります 4。この a−1 を,f(z) の孤立特異点 a における留数 (residue) といい,Res(a; f) で表
こで,孤立特異点 a が n 位の極であるとき
f(z) =
a−n
(z − a)n
+ · · · +
a−1
z − a
+ a0 + a1(z − a) + · · ·
されますから,
(z − a)n
f(z) = a−n + a−n+1(z − a) + · · · + a−1(z − a)n−1
+ a0(z − a)n
+ · · ·
う,べき級数が得られます。したがって,両辺を (n − 1) 回微分すると,
dn−1
dzn−1
(z − a)n
f(z) = (n − 1)!a−1 +
n!
1!
a0(z − a) +
(n + 1)!
2!
a1(z − a)2
+ · · ·
り,
Res(a; f) = a−1 =
1
(n − 1)!
lim
z→a
dn−1
dzn−1
(z − a)n
f(z)
微分によって,a-1 の手前の項まで消える](https://image.slidesharecdn.com/2015aama13slidess-151204092927-lva1-app6891/85/2015-2015-12-17-134-320.jpg)