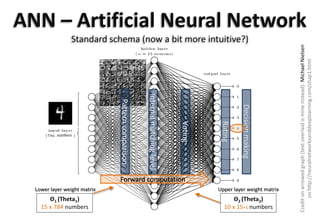
The document provides an overview of how artificial neural networks (ANNs) function, focusing on their ability to learn and recognize patterns, particularly in handwritten digit identification. It uses analogies from human reading and real-world examples like mail sorting to illustrate the underlying concepts and processes involved in ANNs. The content is structured around a presentation given at a Python meetup in Barcelona, emphasizing visual understanding without the use of complex mathematics or coding.

1. Inside the ANN (Artificial Neural Network) A visual and intuitive journey* to understand how it stores knowledge and how it takes decisions*no code, no math included[following BCN Python Group’s request after my presentation on Machine Learning last September 25th2014]
PresentedbyXavier Arrufat
BCN Python Meetup–November2014
Barcelona, November20th, 2014

2. Questions from last Meetup(Python BCN -september25th2014)
1.How does an ANN work? Examples?
2.You must be an engineer… a mathematicianwould never say ANNs are easy [to understand]!

3. Real case
Mail sorting by ZIP (postal) codeNY –1912U.S. Postal ServiceMt.Pleasantsortingoffice –1951TheBritishPostal Museum1960s? Photo Credit: Patrick S. McCabe, U.S. Postal ServiceRoyal Mail on Christmas–Glasgow –2010s? (TheTelegraph–picture: PA) 1990s? U.S. Postal Service

4. Real case
Mail sorting by ZIP (postal) codeRoyal Mail on Christmas –Glasgow –2010s? (TheTelegraph–picture: PA)

5. Agenda
10 minHow humanslearn to read
30 minHow ANNslearn to read (digits)
0 minIs there muchdifference?

6. How humans learn to read
This is letter ‘a’…
A a
4 years old

7. How humans learn to read
And these are letter ‘a’ too…

8. How humans learn to read
Reading test

9. How humans learn to read
Reading test completed: ‘Paranoia’
Easy? Are these really ‘a’s?

10. d b
qp
How humans learn to read
Challenging letters…

11. d b
qp
How humans learn to read
Remark: vertical axed symmetry leads to confusion much more often

12. Human writing at age 4
Notice: only vertical axed symmetry gets (spontaneously) generated

13. Vision circuitry
Observe symmetric ‘wiring’ (only in one plane, I infer)
http://webvision.med.utah.edu/book/part-ix- psychophysics-of-vision/the-primary-visual-cortex/
http://www1.appstate.edu/~kms/classes/ psy3203/EyePhysio/VisualPathways.jpg

14. Real case
Mail sorting by ZIP (postal) codeNY –1912U.S. Postal ServiceMt.Pleasantsortingoffice –1951TheBritishPostal Museum1960s? Photo Credit: Patrick S. McCabe, U.S. Postal ServiceRoyal Mail on Christmas–Glasgow –2010s? (TheTelegraph–picture: PA) 1990s? U.S. Postal Service

15. MNIST dataset
http://yann.lecun.com/exdb/mnist/
Training set of 60,000 examples (6,000 per digit)
Test set of 10,000 examples (1,000 per digit)
Each character is a 28x28 pixel box =>
784 numbers per character within range [0:white, background, 255:black, foreground]
(N.B.: when using ANNs, normalize values to range [0,1] or [-1,1] before continuing)

16. Machine Learning
Problem definition –handwritten digits identification
Input0123456789
Whoseclassdoesitbelong?
(classificationproblem)

17. Machine Learning
Expected solution: probabilistic
Input0123456789
Whoseclassdoesitbelong?
(classificationproblem)
Probability
0.01
0.10
0.07
0.06
0.31
0.04
0.03
0.15
0.02
0.21

18. Machine Learning
What’s the solving black box like?
Input
28 x 28 pixel box
784numbers0123456789Machine Learning-Black Box -
Probability
0.01
0.10
0.07
0.06
0.31
0.04
0.03
0.15
0.02
0.21

19. ANN –Artificial Neural Network
Standard schema (scaring, huh?) Forward computationLowerlayerweightmatrixUpperlayerweightmatrix
numbers
Θ1 (Theta1)
15 x 784 numbers
Θ2 (Theta2)
10 x 15+1numbers
Credit on directed graph (text overlaid is mine instead): Michael Nielsenon http://neuralnetworksanddeeplearning.com/chap1.html

20. Digression
Cellulose acetate

21. Cellulose acetate
Replaced by PET nowadays
(Polyethylene terephthalate a.k.a. ‘polyester’)
Image from Unimed(http://unimed.eu.com/products/radiology- supplies/x-ray-film-cassette-with-screen-4682.html)

22. Semitransparent patternsImage1Image2

23. Semitransparent patternsImage1Image2
0.00
0.50
0.00
0.50
1.00
0.50
0.00
0.50
0.00
0.00
0.00
0.00
0.50
1.00
0.50
0.50
0.50
0.50‘Transparency’ values(foodforthoughtto complete theanalogy: ifnegativevalues, thefilm emitslight insteadof absorbingit?)

24. Superposing patternsImage1Image2SuperposeResult

25. Superposing mathImage1Image2SuperposeResult
0.00
0.50
0.00
0.50
1.00
0.50
0.00
0.50
0.00
0.00
0.00
0.00
0.25
1.00
0.25
0.00
0.25
0.00
0.00
0.00
0.00
0.50
1.00
0.50
0.50
0.50
0.50multiplicationPixelbypixel

26. ‘Coincidence’ levelImage1Image2Result

27. Machine Learning
What’s the solving black box like?
Input
28 x 28 pixel box
784numbers0123456789Machine Learning-Black Box -
Probability
0.01
0.10
0.07
0.06
0.31
0.04
0.03
0.15
0.02
0.21

28. Internal ‘sensors’
(or filters, or bases, or internal features, or neurons … or lower layer)
Sensor commitee1: 20 membersImage fromSheng-huaZhong, Yan Liu, Yang Liu. Bilinear Deep Learning for Image Classification. To appear in ACM International Conference of Multimedia (SIG MM'11), 2011

29. Internal ‘sensors’
(or filters, or bases, or internal features, or neurons … or lower layer)
Sensor commitee1: 20 membersImages fromSheng-huaZhong, Yan Liu, Yang Liu. Bilinear Deep Learning for Image Classification. To appear in ACM International Conference of Multimedia (SIG MM'11), 2011

30. Internal ‘sensors’
(or filters, or bases, or internal features, or neurons …)
Sensor commitee2: 900 members
Sensor commitee3: 64 members
Image from Pikalike
http://www.picalike.com/
Image from Tom Lahore http://evolvingstuff.blogspot.com.es/2012/12/mnist-features.html

31. Internal sensors
(reduced selection for the sake of simplicity) ‘Neurons’ extracted from Pikalike’simage on previous page
http://www.picalike.com/

32. Internal sensors: matching input
Levelof response as per patternmatching
Input
high
low
mid
mid
low
mid
low
low

33. Internal sensors: voting0123456789
‘Sensor commitee’
(response as per patternmatching)
Individual ‘votes’
high
low
mid
mid
low
mid
low
low
0.70
0.80
0.12
0.11
0.85
0.03
0.32
0.65
0.15
0.08
Input
Note: all numbersin thisslidearemadeup. Theydo notcorrespondto actual results.

34. Internal sensors: voting0123456789
‘Votingcommitee’
(as per patternrecognition)
Cumulated‘votes’
high
low
mid
mid
low
mid
low
low
2.42
20.40
15.73
12.52
63.61
7.93
6.06
2.94
4.11
41.56
Input
Note: all numbersin thisslidearemadeup. Theydo notcorrespondto actual results.

35. Normalizing votes (probability) 0123456789
‘Votingcommitee’
(as per patternrecognition)
Cumulated‘votes’
high
low
mid
mid
low
mid
low
low
2.42
20.40
15.73
12.52
63.61
7.93
6.06
2.94
4.11
41.56
Input
0.01
0.10
0.07
0.06
0.31
0.04
0.03
0.15
0.02
0.21
Probability
(votes / total)
Note: all numbersin thisslidearemadeup. Theydo notcorrespondto actual results.

36. Decision making0123456789
‘Votingcommitee’
(as per patternrecognition)
Cumulated‘votes’
high
low
mid
mid
low
mid
low
low
2.42
20.40
15.73
12.52
63.61
7.93
6.06
2.94
4.11
41.56
Input
0.01
0.10
0.07
0.06
0.31
0.04
0.03
0.15
0.02
0.21
Probability
(votes / total)
Note: all numbersin thisslidearemadeup. Theydo notcorrespondto actual results.

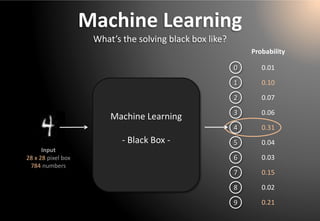
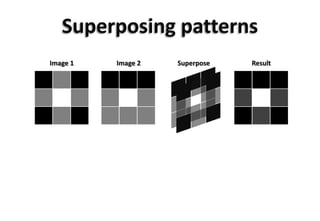
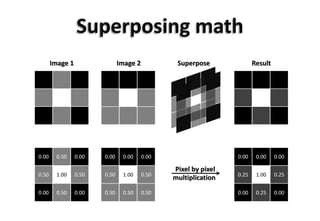
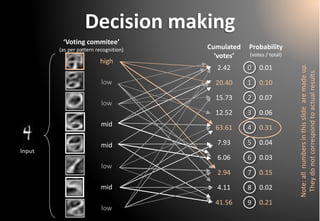
37. All steps in one page
0.0
0.9
*
=
0.00.90.9
*
=0.8
Σ
1) Multiplyinput * filter, pixelper pixel
2) Addup resultingvalues. Youget a simple real numberR
4) Cast weighted votes on your filter’s favorite classes
7.35
Input
Filter
3) (optional–non-lineal activationfunction) SquashR withintherange(0,1) [ or (-1,1) ]
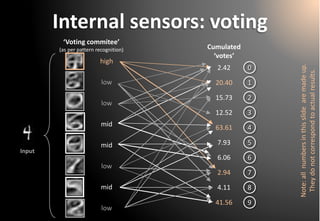
Note: all numbersin thisslidearemadeup. Theydo notcorrespondto actual results.
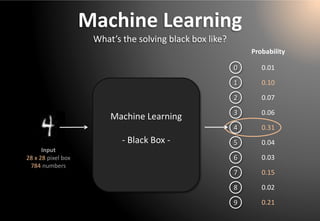
5) Normalize votes: compute class probabilities
6) Make a decisionbased on probabilites
0) Get a convenient set of filtersandvotingrules(a.k.a. ‘ANN training’)

38. ANN –Artificial Neural Network
Standard schema (now a bit more intuitive?)
Θ1 (Theta1)
15 x 784 numbers
Θ2 (Theta2)
10 x 15+1numbersLowerlayerweightmatrixUpperlayerweightmatrix RatingDecisionmaking Forward computation PatterncomparisonInternalmatchinglevelVoting
numbers
Credit on arrowed graph (text overlaid is mine instead): Michael Nielsenon http://neuralnetworksanddeeplearning.com/chap1.html

39. Q & A