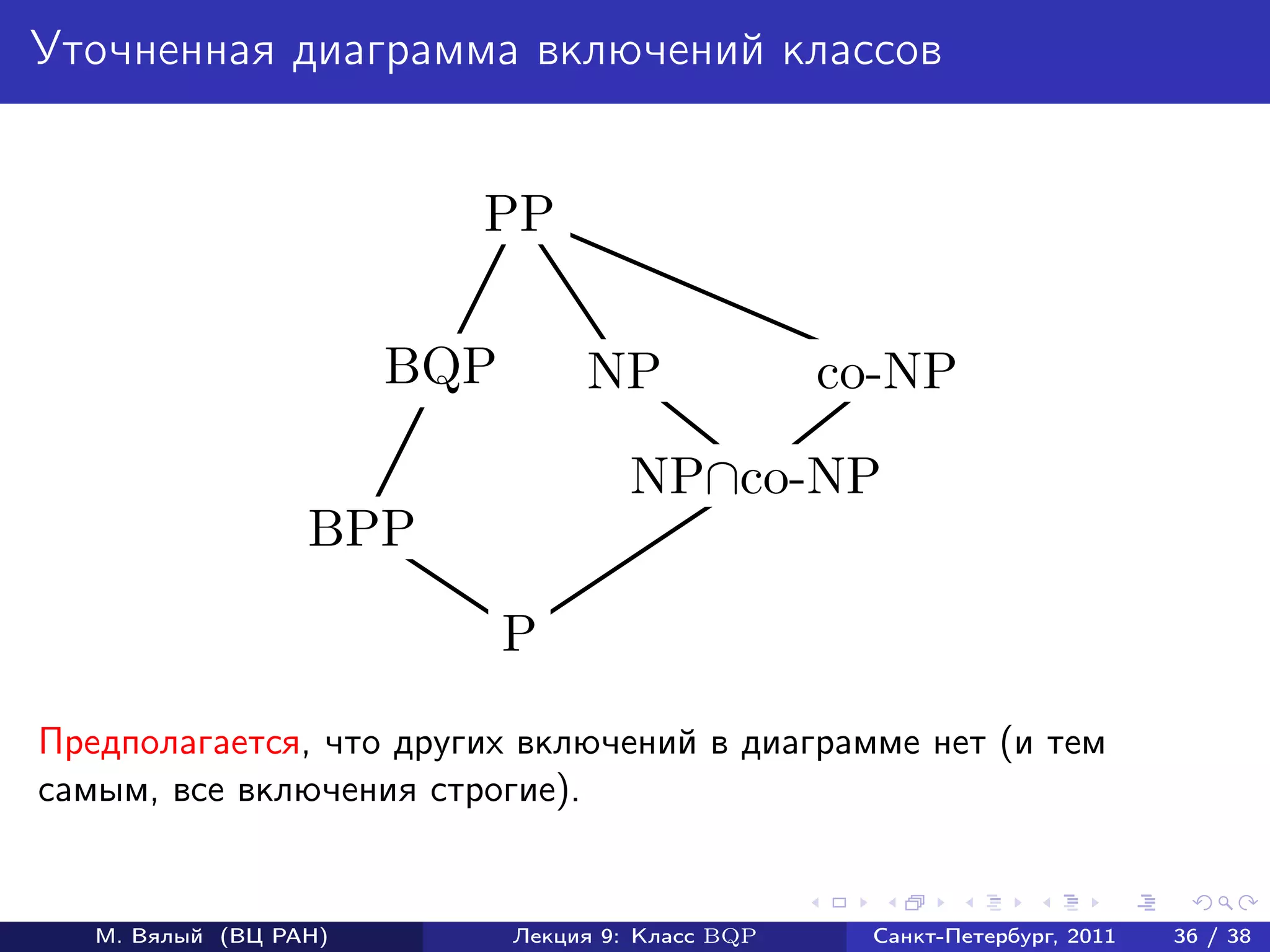
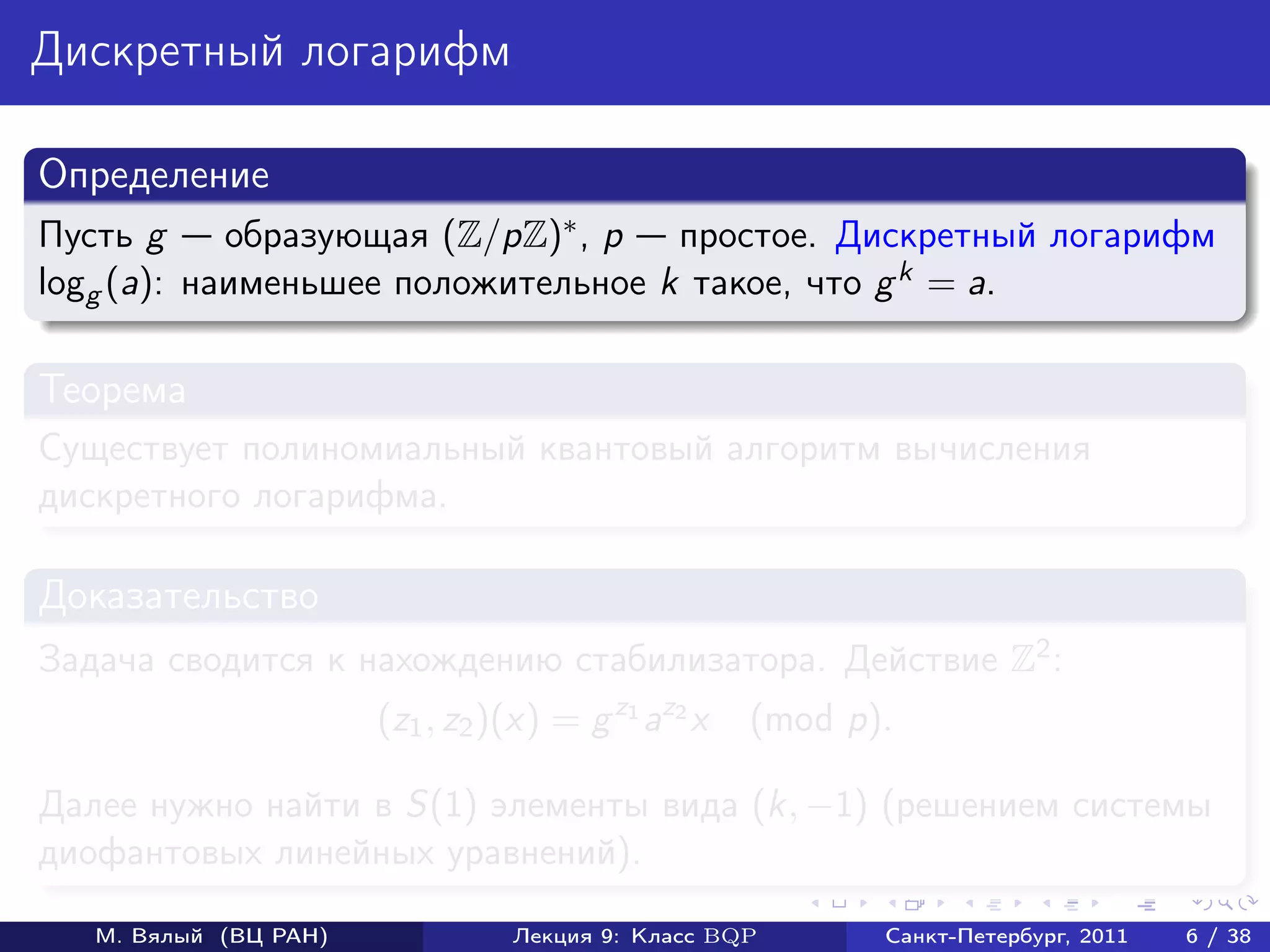
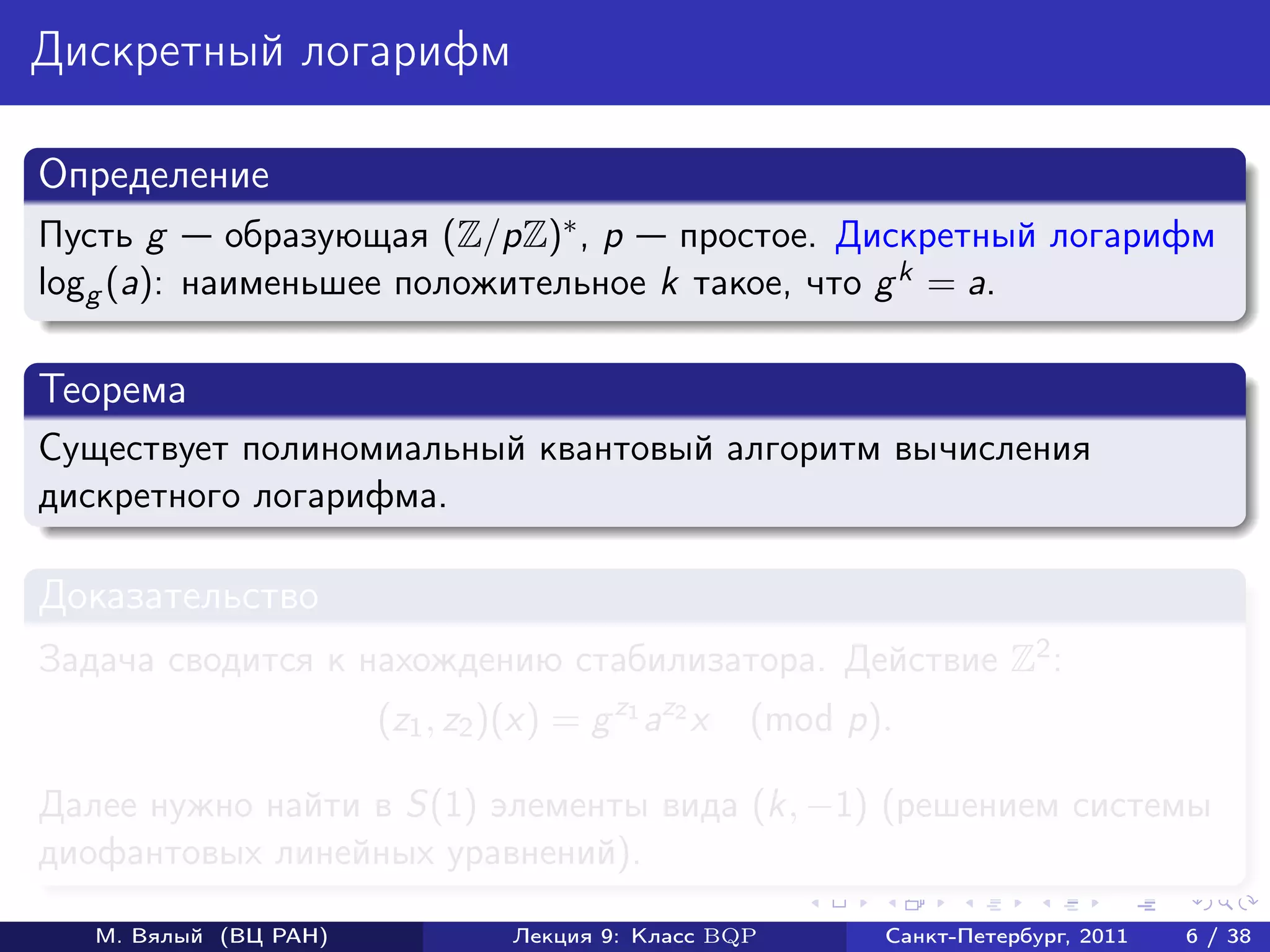
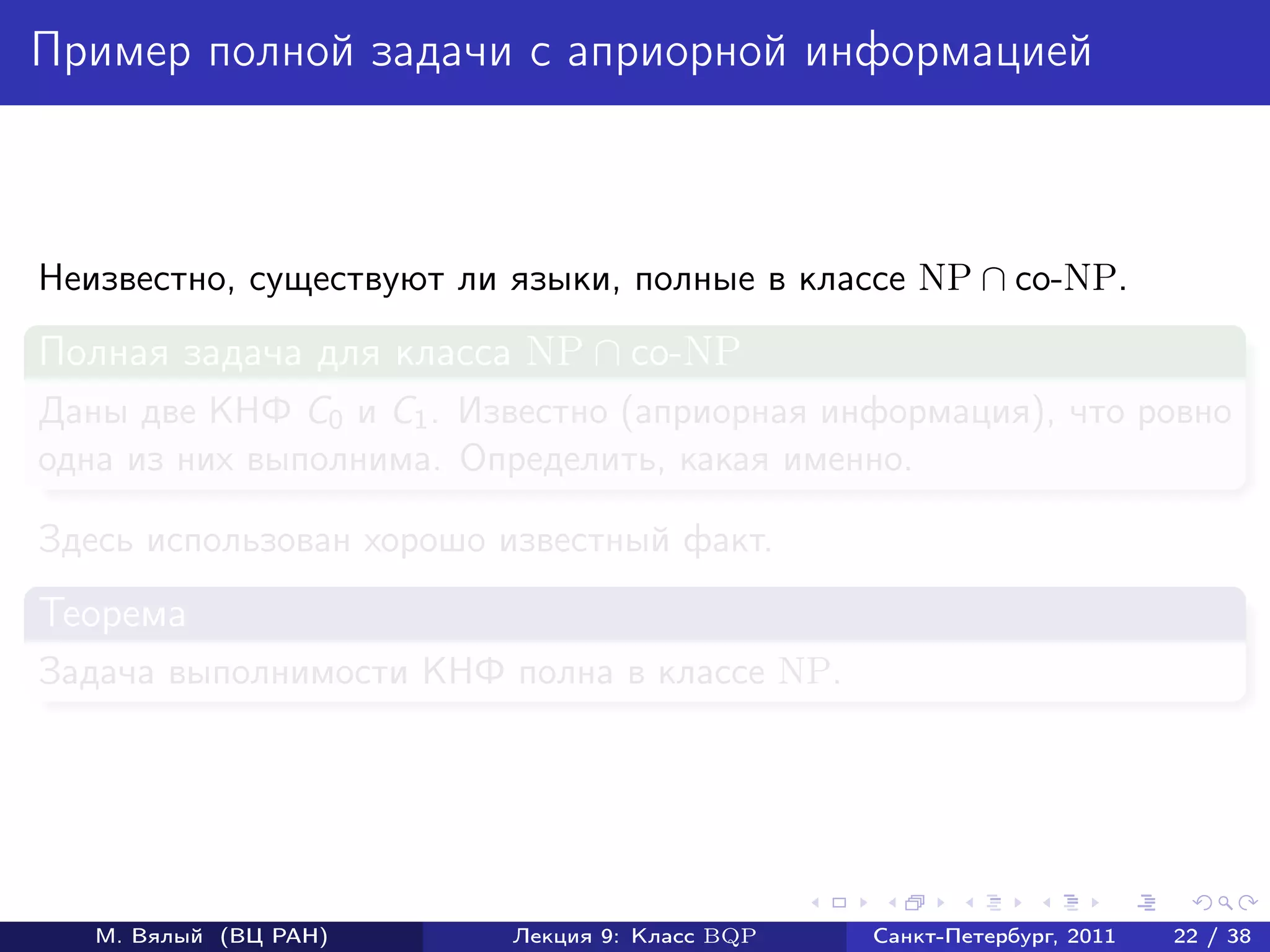
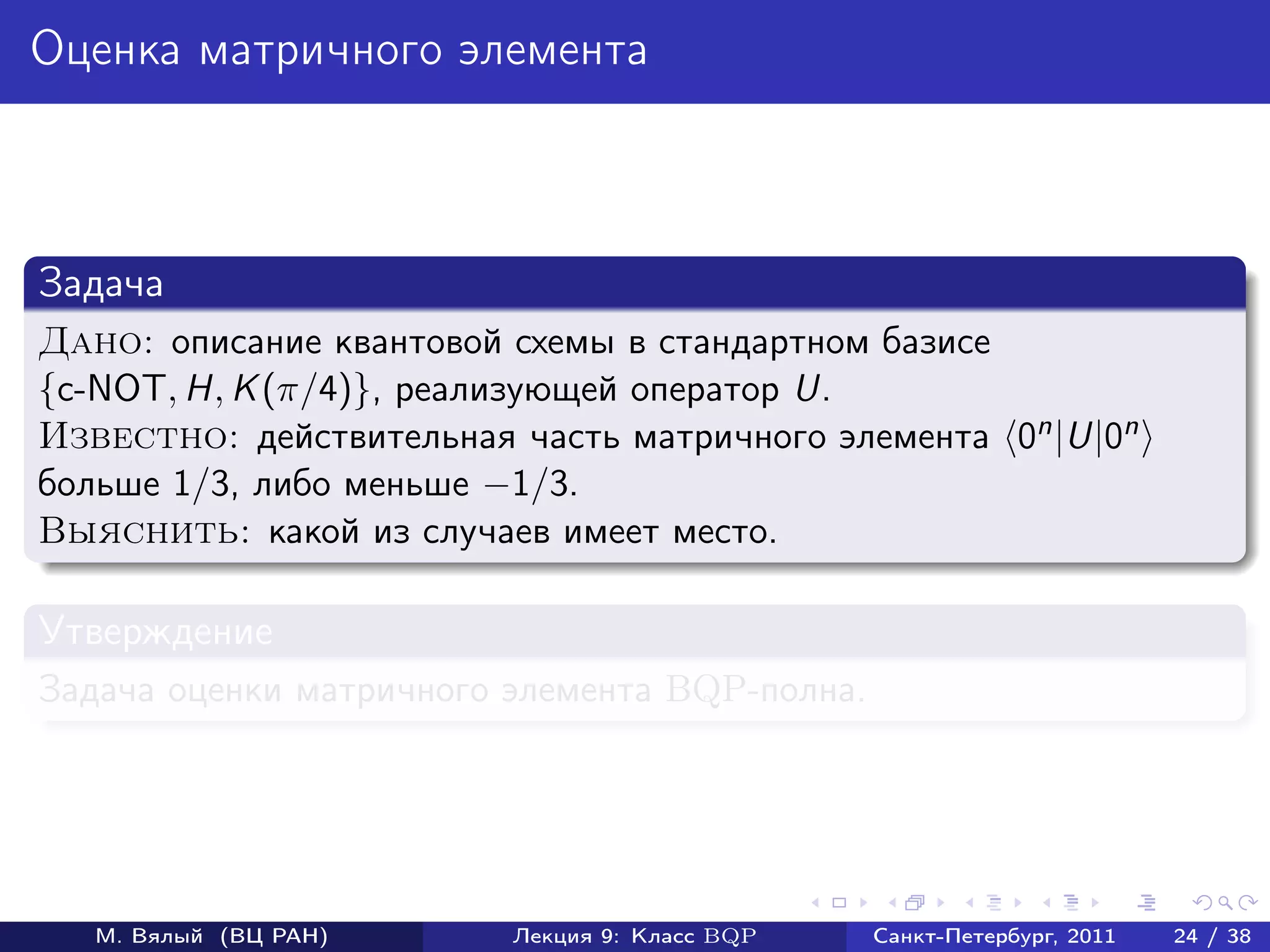
Документ охватывает классы квантовых алгоритмов, в частности BQP, и их взаимосвязь с классическими алгоритмами сложности. Он рассматривает примеры эффективных квантовых алгоритмов, включая алгоритмы для нахождения стабилизаторов и вычисления дискретного логарифма. Также обсуждаются открытые вопросы в области квантовых вычислений и трудности решений некоторых связанных задач.




















































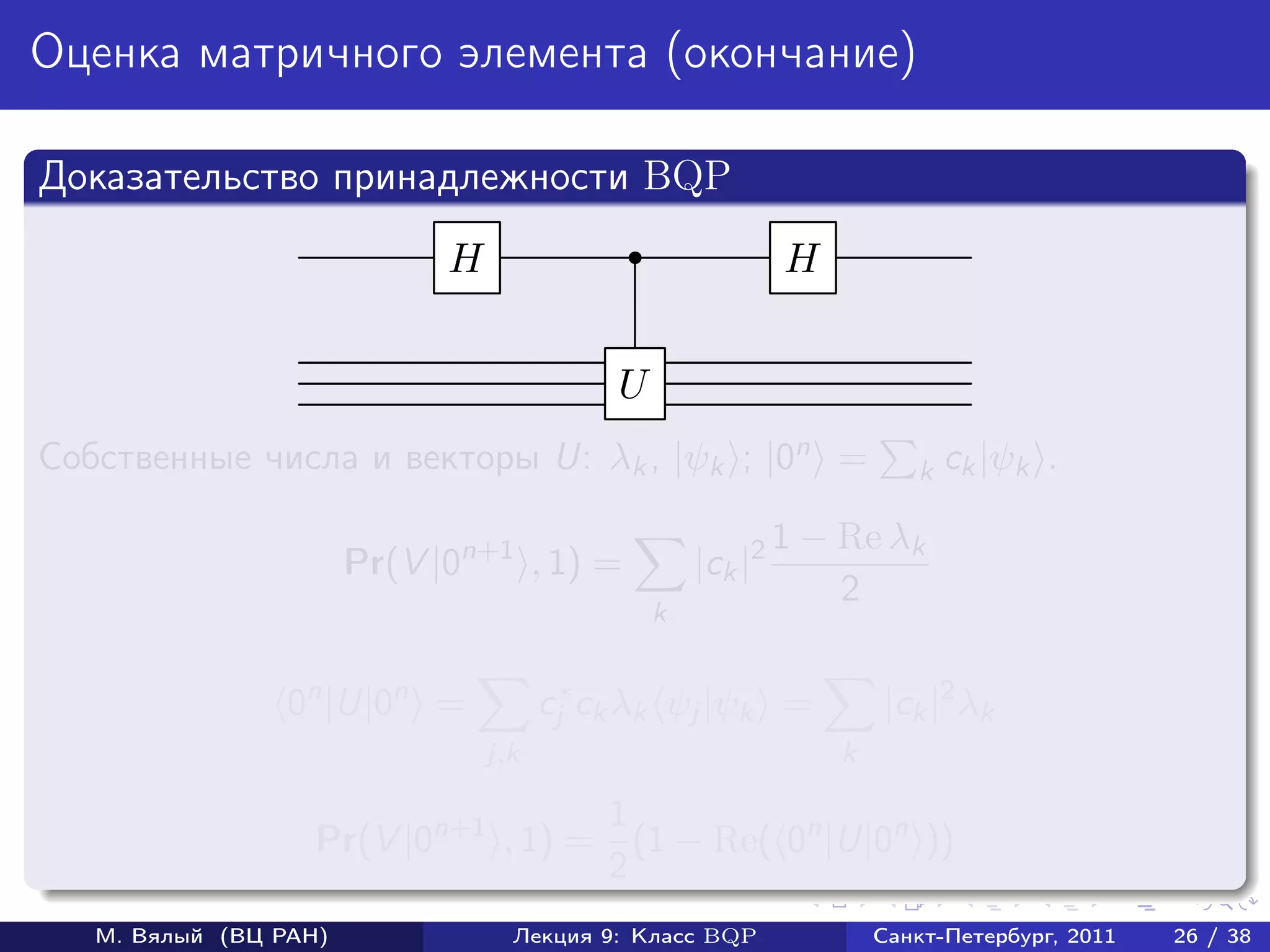
![Оценка матричного элемента (продолжение)
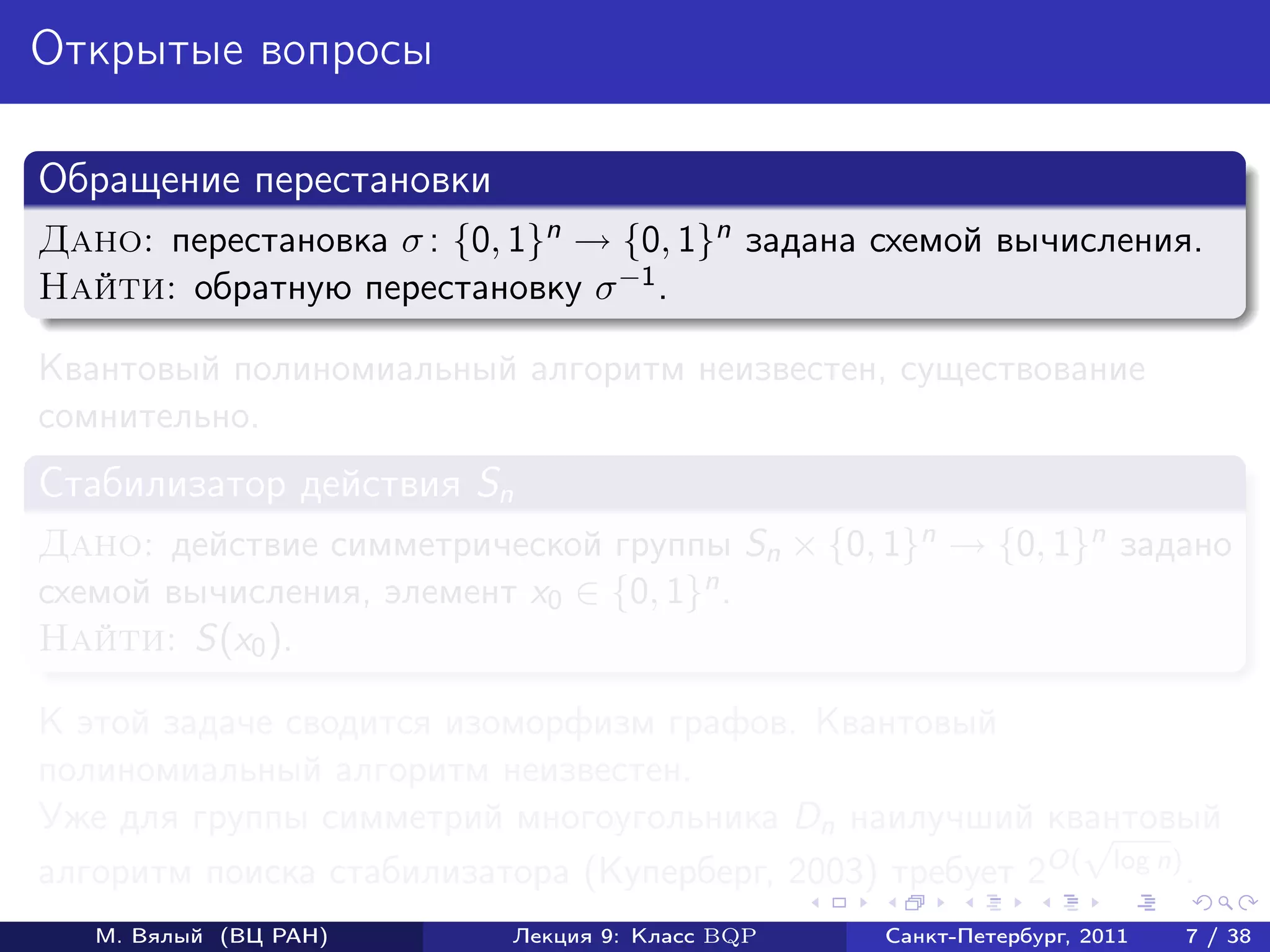
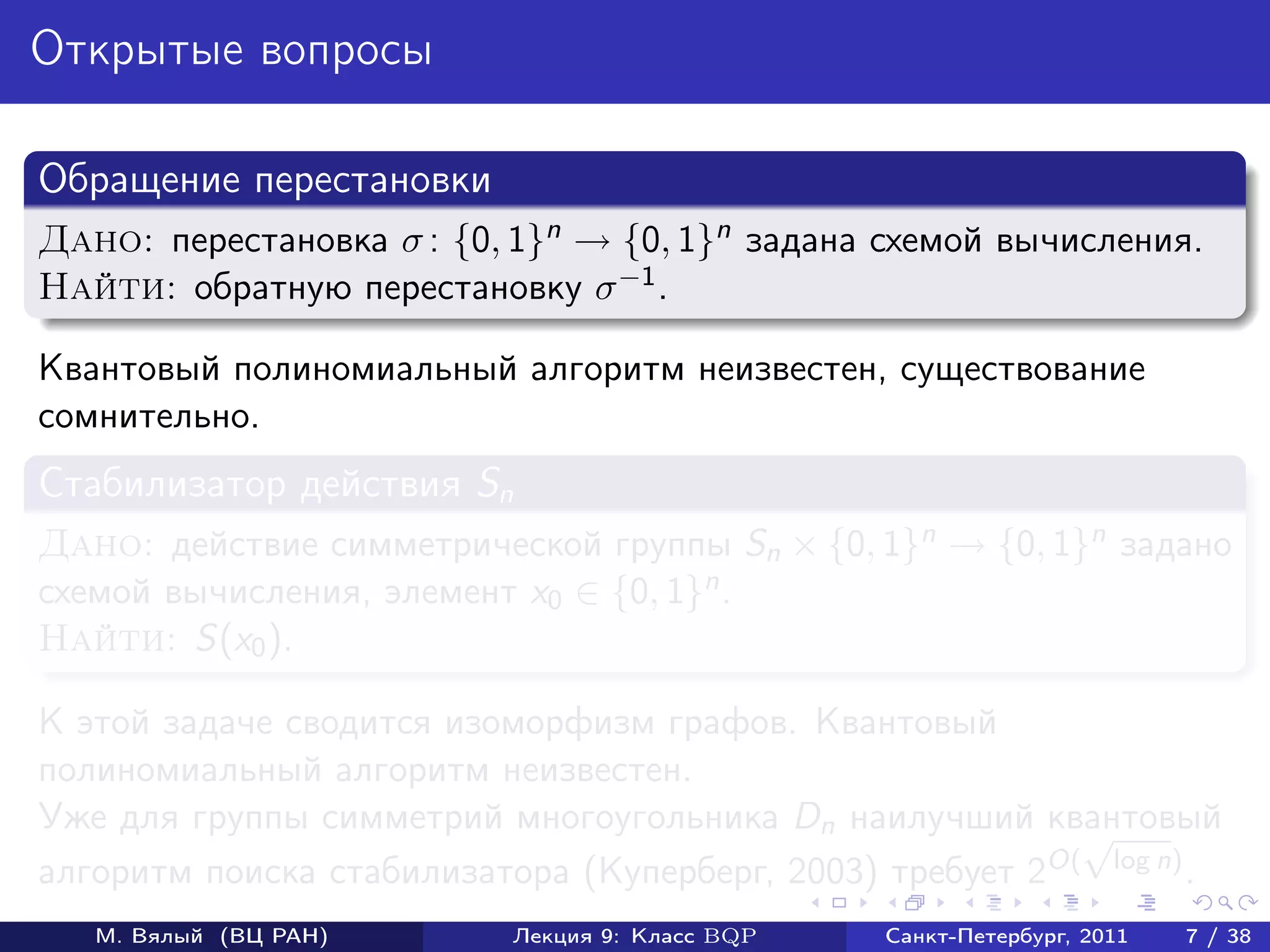
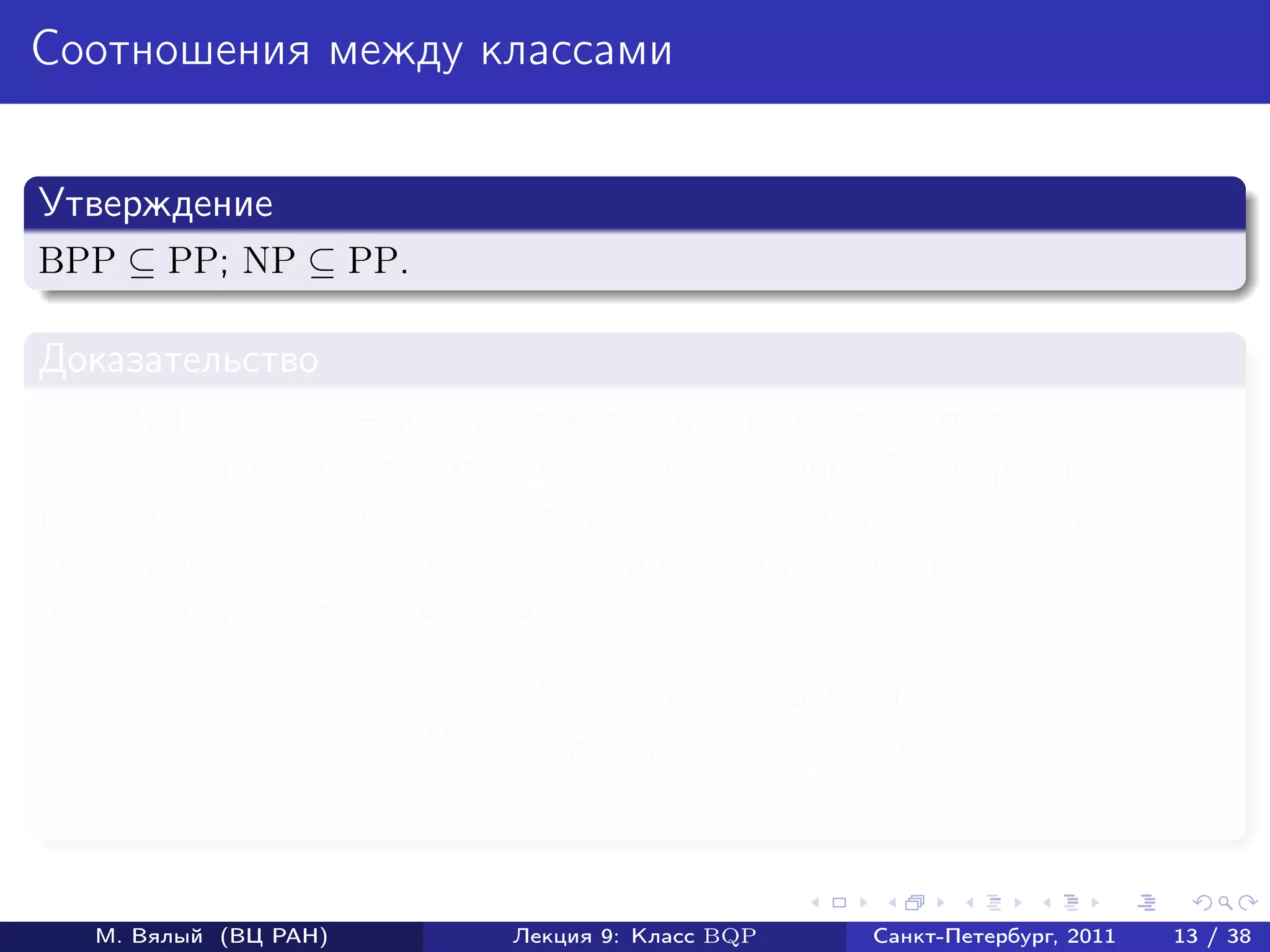
Доказательство BQP-трудности
Пусть U оператор, реализуемый схемой, для которой нужно оценить
вероятность p наблюдения 1 в первом кубите.
Докажем, что для V = U † σz [1]U выполняется равенство
0n |V |0n = 1 − 2p.
Пусть U|0n = |0 ⊗ |ψ0 + |1 ⊗ |ψ1 .
Тогда
0n |V |0n = 0n |U † σz [1]U|0n = ψ0 |ψ0 − ψ1 |ψ1 = 1 − 2p.
Осталось заметить, что p < 1/3 влечет 0n |V |0n > 1/3, а p > 2/3
влечет 0n |V |0n < −1/3.
М. Вялый (ВЦ РАН) Лекция 9: Класс BQP Санкт-Петербург, 2011 25 / 38](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture09-110415020600-phpapp01/75/20110409-quantum-algorithms_vyali_lecture09-65-2048.jpg)
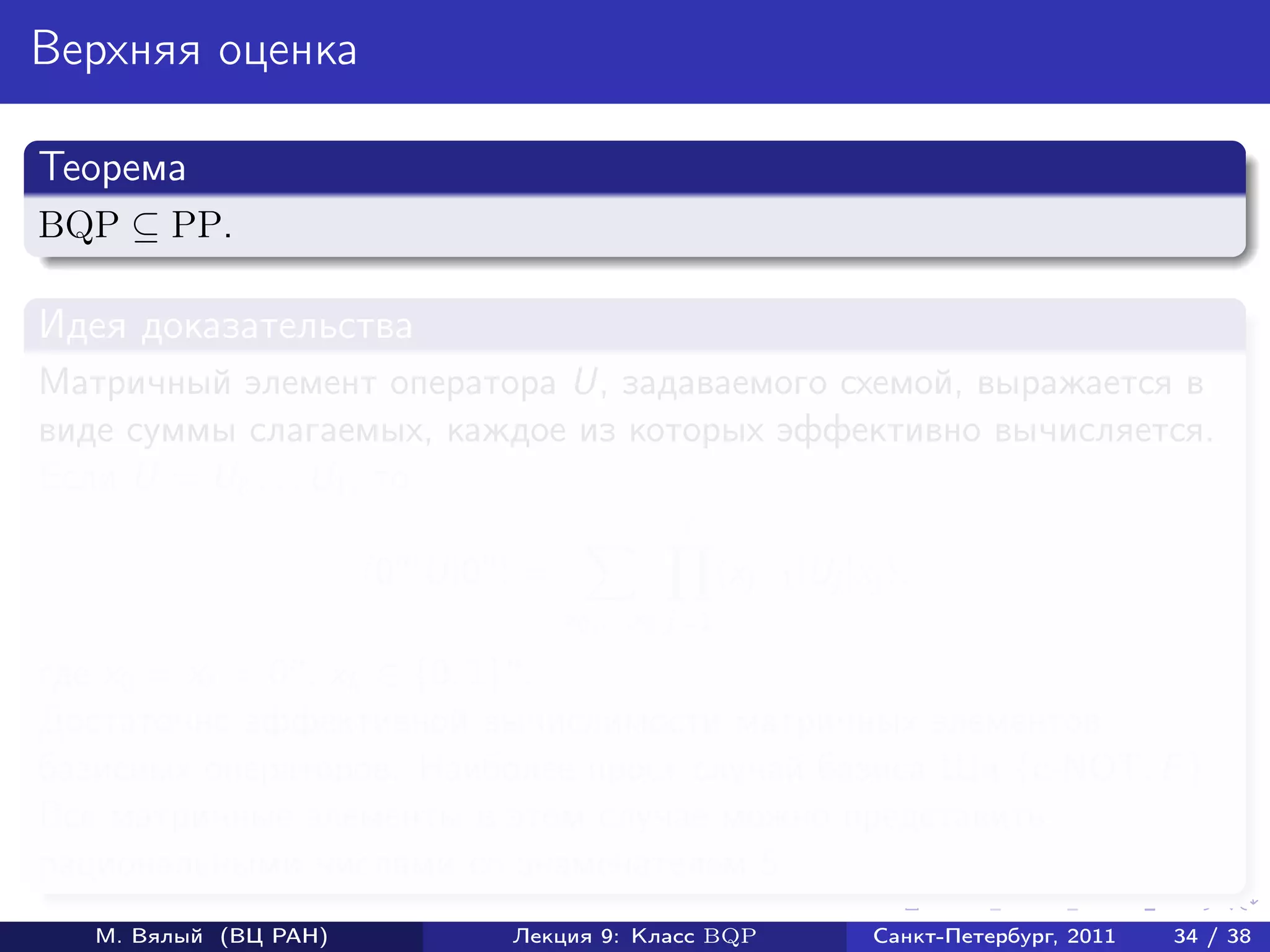
![Оценка матричного элемента (продолжение)
Доказательство BQP-трудности
Пусть U оператор, реализуемый схемой, для которой нужно оценить
вероятность p наблюдения 1 в первом кубите.
Докажем, что для V = U † σz [1]U выполняется равенство
0n |V |0n = 1 − 2p.
Пусть U|0n = |0 ⊗ |ψ0 + |1 ⊗ |ψ1 .
Тогда
0n |V |0n = 0n |U † σz [1]U|0n = ψ0 |ψ0 − ψ1 |ψ1 = 1 − 2p.
Осталось заметить, что p < 1/3 влечет 0n |V |0n > 1/3, а p > 2/3
влечет 0n |V |0n < −1/3.
М. Вялый (ВЦ РАН) Лекция 9: Класс BQP Санкт-Петербург, 2011 25 / 38](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture09-110415020600-phpapp01/75/20110409-quantum-algorithms_vyali_lecture09-66-2048.jpg)
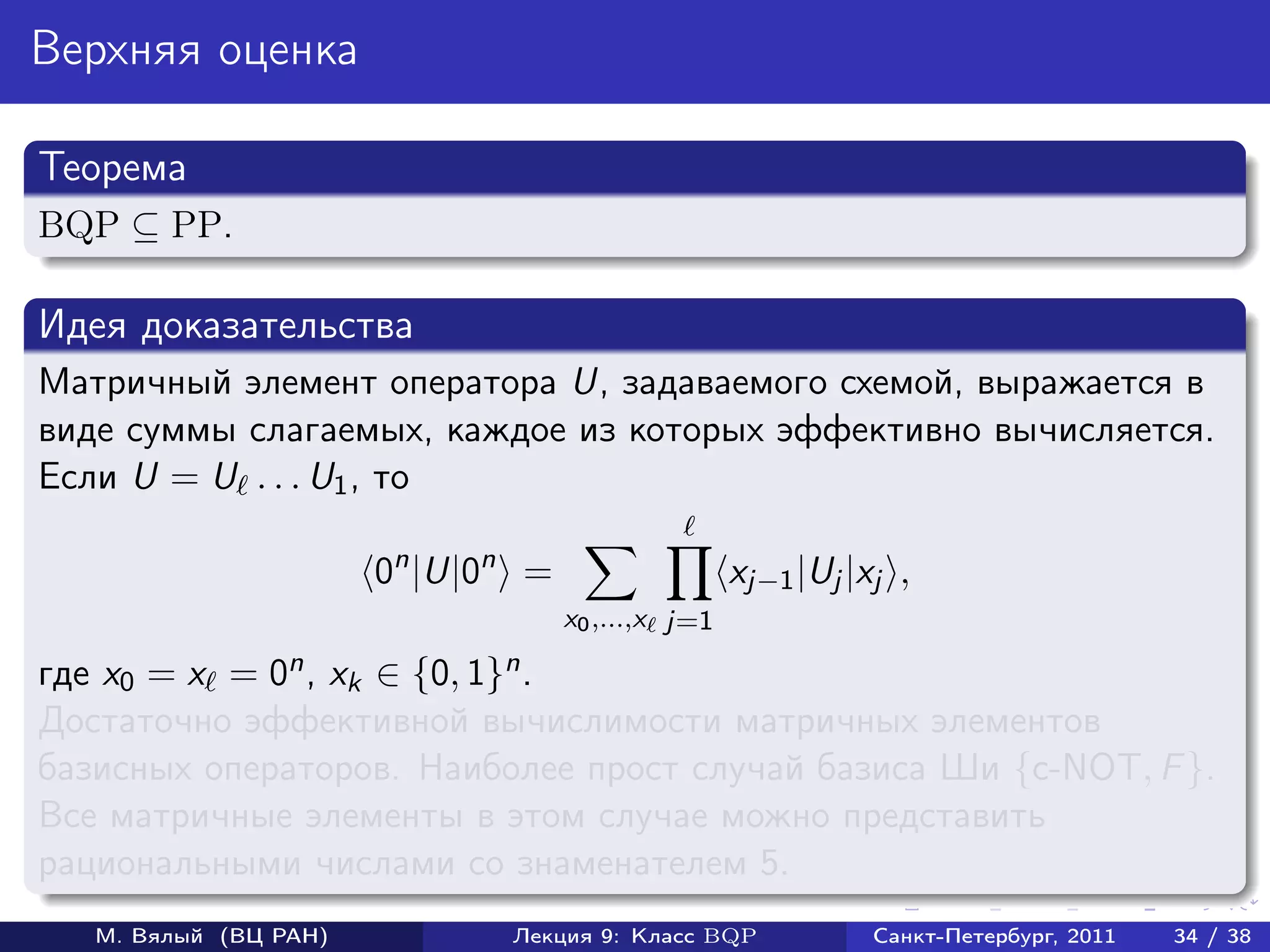
![Оценка матричного элемента (продолжение)
Доказательство BQP-трудности
Пусть U оператор, реализуемый схемой, для которой нужно оценить
вероятность p наблюдения 1 в первом кубите.
Докажем, что для V = U † σz [1]U выполняется равенство
0n |V |0n = 1 − 2p.
Пусть U|0n = |0 ⊗ |ψ0 + |1 ⊗ |ψ1 .
Тогда
0n |V |0n = 0n |U † σz [1]U|0n = ψ0 |ψ0 − ψ1 |ψ1 = 1 − 2p.
Осталось заметить, что p < 1/3 влечет 0n |V |0n > 1/3, а p > 2/3
влечет 0n |V |0n < −1/3.
М. Вялый (ВЦ РАН) Лекция 9: Класс BQP Санкт-Петербург, 2011 25 / 38](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture09-110415020600-phpapp01/75/20110409-quantum-algorithms_vyali_lecture09-67-2048.jpg)
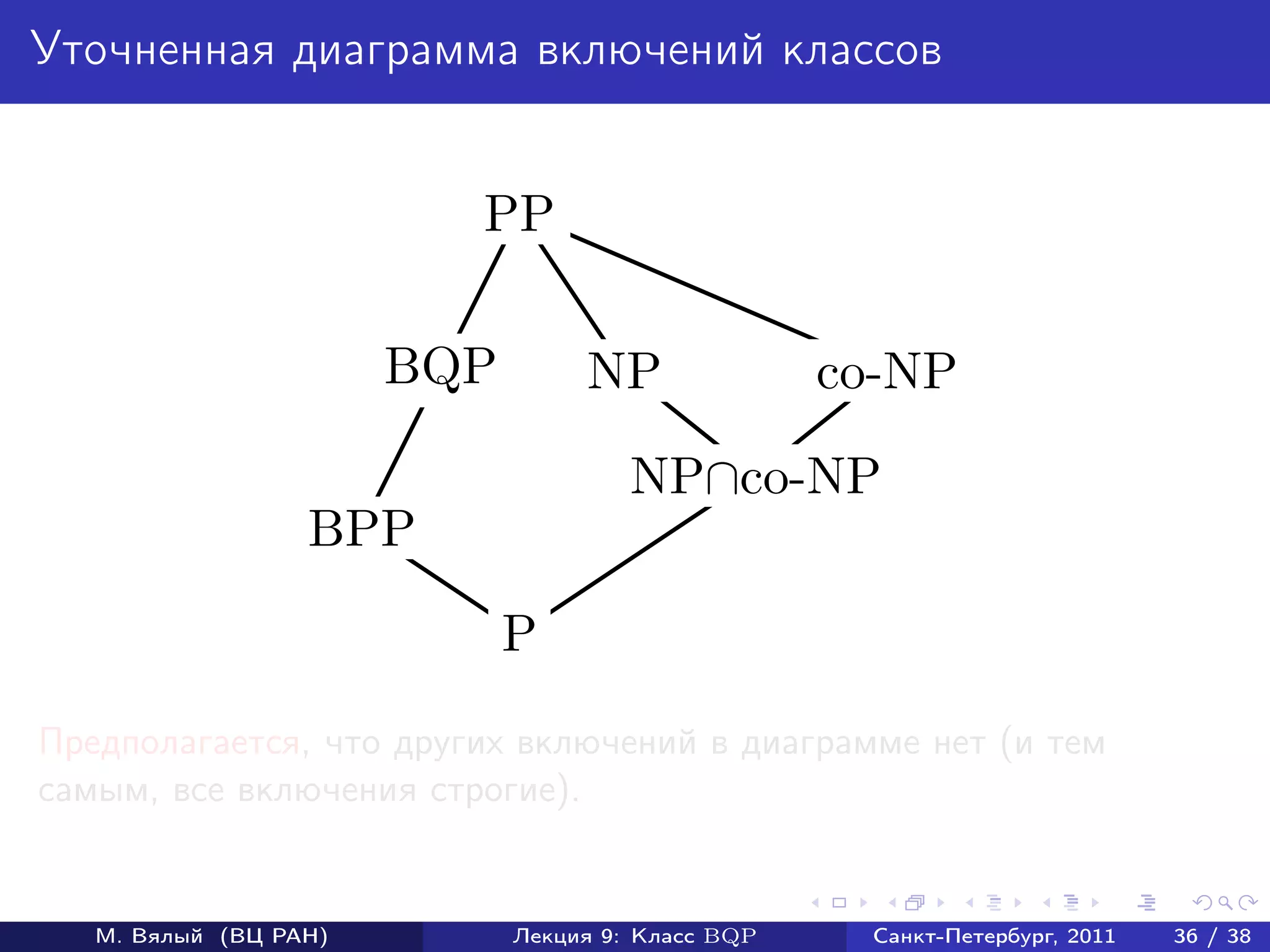
![Оценка матричного элемента (продолжение)
Доказательство BQP-трудности
Пусть U оператор, реализуемый схемой, для которой нужно оценить
вероятность p наблюдения 1 в первом кубите.
Докажем, что для V = U † σz [1]U выполняется равенство
0n |V |0n = 1 − 2p.
Пусть U|0n = |0 ⊗ |ψ0 + |1 ⊗ |ψ1 .
Тогда
0n |V |0n = 0n |U † σz [1]U|0n = ψ0 |ψ0 − ψ1 |ψ1 = 1 − 2p.
Осталось заметить, что p < 1/3 влечет 0n |V |0n > 1/3, а p > 2/3
влечет 0n |V |0n < −1/3.
М. Вялый (ВЦ РАН) Лекция 9: Класс BQP Санкт-Петербург, 2011 25 / 38](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture09-110415020600-phpapp01/75/20110409-quantum-algorithms_vyali_lecture09-68-2048.jpg)