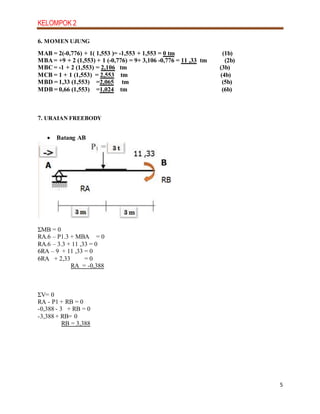
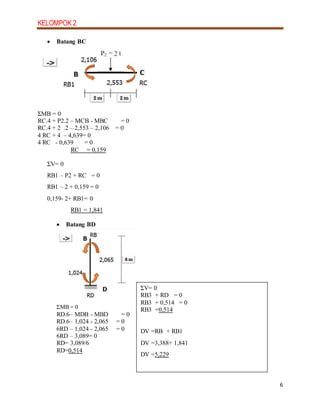
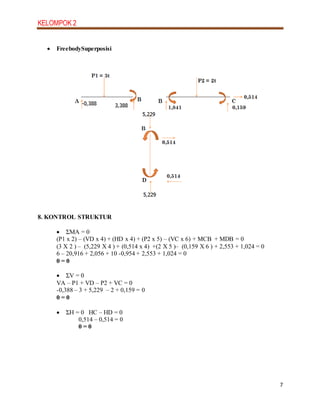
1. The document analyzes the structure of a plane frame using the slope deflection method. It presents the problem of a portal frame under loading and goes through the steps of the slope deflection method. 2. The steps include determining degrees of freedom, member forces, member stiffness, developing the slope deflection equations, solving for unknown slopes, calculating member moments, drawing free body diagrams, and constructing shear and moment diagrams. 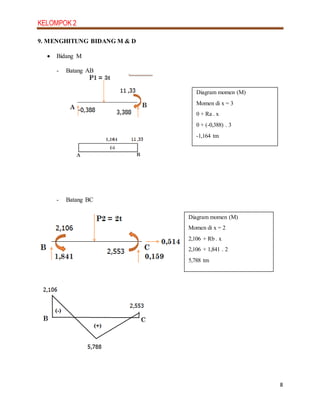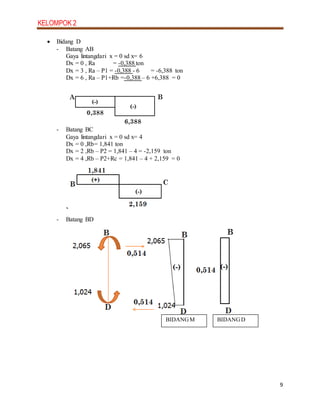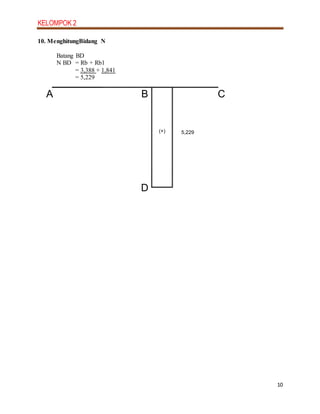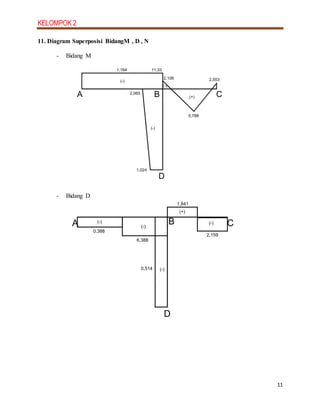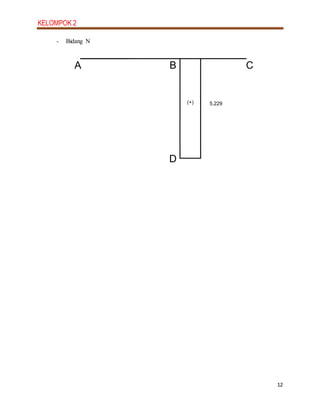3. Diagrams are presented for the shear, moment and axial force (N) diagrams, showing the distribution of these effects along each member of the frame.

1. KELOMPOK 2
1
ANALISA STRUKTUR
SLOPE DEFLECTION
KELOMPOK 2
MUCHAMAD LUQMAN RAHMAWAN (1561122003)
WAHYU PURNOMO ADI (1561122004)
MADE BAGUS GITA DARMA (1561122005)
UNIVERSITAS WARMADEWA
FAKULTAS TEKNIK
JURUSAN TEKNIK SIPIL

2. KELOMPOK 2
2
METODE SLOPE DEFLECTION
ContohSoal Portal BidangTidakBergoyang (Non-Sway Plane Frame)
Diketahuistruktur portal denganpembebanansepertigambarberikut :
Penyelesaian :
1. Derajat kebebasan dalam pergoyangan struktur statis tak tentu :
n = 2j – (m + 2f + 2h + r)
dengan :
n = jumlah derajat kebebasan (degree of fredom)
j = jumlah titik simpul, termasuk perletakan (joint)
m = jumlah batang yang dibatasi oleh dua joint (member)
f = jumlah perletakan jepit(fixed)
h = jumlah perletakan sendi (hinged)
r = jumlah perletakan rol (roll)
Cek: n = 2x4 – (3 + 2x2 + 2x0 + 1)
= 8 – 8 = 0 ≤0 →tidak ada pergoyangan

3. KELOMPOK 2
3
2. MENENTUKAN JUMLAH VARIABEL YANG ADA :
- A = rol, θA bukan variabel
- B = titik simpul, ada variable θB
- C = jepit, θC= 0
- D = jepit, θD=0
- Jadi variabelnya hanya satu, θB
3. PERHITUNGAN MOMEN PRIMER DAN KEKAKUAN BATANG
Momen primer
MF
BA = + 3/16 PL = + 3/16 (3) 6 = + 9 tm
MF
BC = - 1/8 PL = - 1/8 (2) 4 = - 1 tm
MF
CB = + 1/8 PL = + 1/8 (2) 4 = + 2 tm
Kekakuan batang
KBA = 3EI/L = 3(2EI)/6 = 1 EI
KBC = KCB = 4EI/L = 4(EI)/4 = 1 EI
KBD = KDB = 4EI/L = 4(EI)/6 = 0,66 EI
4. PERSAMAAN SLOPE DEFLECTION
MAB = M°AB + 1 EI (2θA + θB) = 0 + 2 EIθA + 1 EIθB (1)
MBA = M°BA + 1 EI (2θB + θA) = +9 + 2 EIθB + 1 EIθA (2)
MBC = M°BC + 1 EI (2θB + θC) = -1 + 2 EIθB + 1 EIθC (3)
MCB = M°CB + 1 EI (2θC + θB) = 1 + 2 EIθC + 1 EIθB (4)
MBD = M°BD + 0,66 EI (2θB + θD) = 0 + 1,33 EIθB + 0,66 EIθD (5)
MDB = M°DB + 0,66 EI (2θD + θB) = + 0 + 1,33 EIθD + 0,66 EIθB (6)
Syaratbatas (boundary condition) :
- C = jepit, θC=0
- D = jepit, θD=0
- A = rol, MAB =0

4. KELOMPOK 2
4
PERSMAAN SLOPE DEFLECTION MENJADI
0 =2 EIθA + 1 EIθB (1a)
MBA =9 + 2 EIθB + 1 EIθA (2a)
MBC = -1 + 2 EIθB (3a)
MCB = 1 + 1 EIθB (4a)
MBD = 1,33 EIθB (5a)
MDB = 0,66 EIθB (6a)
5. MENCARI NILAI θ B
Σ Mb = 0
(2a) + (3a) + (5a) = 0
(9 + 2 EIθB + 1 EIθA) +(-1 + 2 EIθB ) + (1,33 EIθB ) = 0
(+8+ 5,33 EI θB + 1EI θA) = 0
1EI θA + 5,33 EI θB = -8 (7)
Eliminasi – substitusi persamaan 1a dengan persamaan 7
1EI θA + 5,33 EI θB = -8 x 2 2EI θA + 10,66EI θB = 16
2EIθA + 1 EIθB = 0 x 1 2 EIθA + 1 EIθB = 0 -
9,66 EIθB = 16
EIθB =1,553
Substitusi EIθB ke persamaan 1a
2 EIθA + 1 EIθB = 0
2 EIθA + 1( 1,553 )= 0
2 EIθA + 1,553 = 0
EIθA = -0,776

5. KELOMPOK 2
5
6. MOMEN UJUNG
MAB = 2(-0,776) + 1( 1,553 )= -1,553 + 1,553 = 0 tm (1b)
MBA = +9 + 2 (1,553) + 1 (-0,776) = 9+ 3,106 -0,776 = 11 ,33 tm (2b)
MBC = -1 + 2 (1,553) = 2,106 tm (3b)
MCB = 1 + 1 (1,553) = 2,553 tm (4b)
MBD = 1,33 (1,553) =2,065 tm (5b)
MDB = 0,66 (1,553) =1,024 tm (6b)
7. URAIAN FREEBODY
 Batang AB
ΣMB = 0
RA.6 – P1.3 + MBA = 0
RA.6 – 3.3 + 11 ,33 = 0
6RA – 9 + 11 ,33 = 0
6RA + 2,33 = 0
RA = -0,388
ΣV= 0
RA - P1 + RB = 0
-0,388 - 3 + RB = 0
-3,388 + RB= 0
RB = 3,388

6. KELOMPOK 2
6
 Batang BC
ΣMB = 0
RC.4 + P2.2 – MCB - MBC = 0
RC.4 + 2 .2 – 2,553 – 2,106 = 0
4 RC + 4 – 4,639= 0
4 RC - 0,639 = 0
RC = 0,159
ΣV= 0
RB1 – P2 + RC = 0
RB1 – 2 + 0,159 = 0
0,159- 2+ RB1= 0
RB1 = 1,841
 Batang BD
ΣMB = 0
RD.6– MDB - MBD = 0
RD.6– 1,024 - 2,065 = 0
6RD – 1,024 - 2,065 = 0
6RD – 3,089= 0
RD= 3,089/6
RD=0,514
ΣV= 0
RB3 + RD = 0
RB3 + 0,514 = 0
RB3 =0,514
DV =RB + RB1
DV =3,388+ 1,841
DV =5,229

7. KELOMPOK 2
7
 FreebodySuperposisi
8. KONTROL STRUKTUR
 ΣMA = 0
(P1 x 2) – (VD x 4) + (HD x 4) + (P2 x 5) – (VC x 6) + MCB + MDB = 0
(3 X 2 ) – (5,229 X 4 ) + (0,514 x 4) +(2 X 5 )– (0,159 X 6 ) + 2,553 + 1,024 = 0
6 – 20,916 + 2,056 + 10 -0,954 + 2,553 + 1,024 = 0
0 = 0
 ΣV = 0
VA – P1 + VD – P2 + VC = 0
-0,388 – 3 + 5,229 – 2 + 0,159 = 0
0 = 0
 ΣH = 0 HC – HD = 0
0,514 – 0,514 = 0
0 = 0

8. KELOMPOK 2
8
9. MENGHITUNG BIDANG M & D
 Bidang M
- Batang AB
- Batang BC
Diagram momen (M)
Momen di x = 3
0 + Ra . x
0 + (-0,388) . 3
-1,164 tm
Diagram momen (M)
Momen di x = 2
2,106 + Rb . x
2,106 + 1,841 . 2
5,788 tm

9. KELOMPOK 2
9
 Bidang D
- Batang AB
Gaya lintangdari x = 0 sd x= 6
Dx = 0 , Ra = -0,388 ton
Dx = 3 , Ra – P1 = -0,388 - 6 = -6,388 ton
Dx = 6 , Ra – P1+Rb =-0,388 – 6 +6,388 = 0
- Batang BC
Gaya lintangdari x = 0 sd x= 4
Dx = 0 ,Rb= 1,841 ton
Dx = 2 ,Rb – P2 = 1,841 – 4 = -2,159 ton
Dx = 4 ,Rb – P2+Rc = 1,841 – 4 + 2,159 = 0
- Batang BD
BIDANGM BIDANGD

10. KELOMPOK 2
10
10. MenghitungBidang N
Batang BD
N BD = Rb + Rb1
= 3,388 + 1,841
= 5,229
A B C
D
5,229(+)

11. KELOMPOK 2
11
11. Diagram Superposisi BidangM , D , N
- Bidang M
- Bidang D
A B C
D
(-)
1,164 11,33
2,106
(-)
5,788
(+)
2,553
1,024
2,065
(-)
A B C
D
(-)
(-)
0,388
6,388
(+)
1,841
(-)
2,159
(-)0,514

12. KELOMPOK 2
12
- Bidang N
A B C
D
5,229(+)