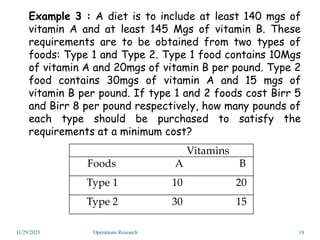
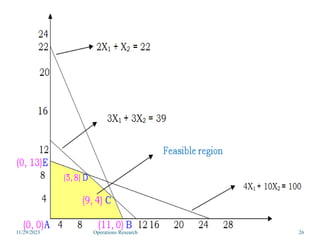
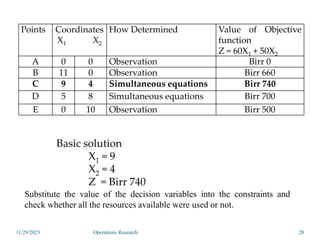
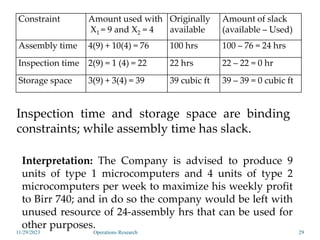
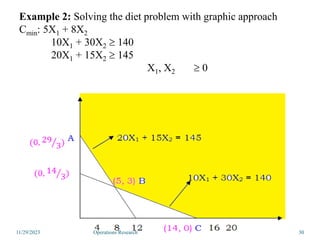
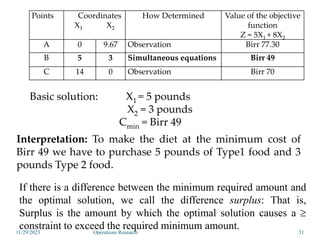
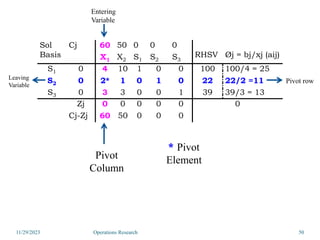
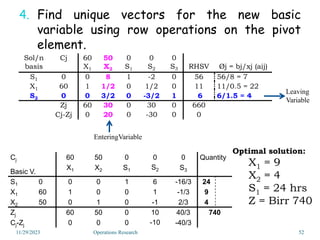
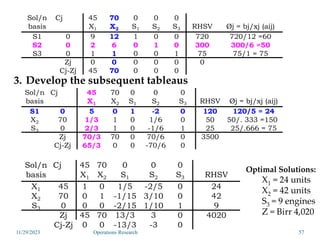
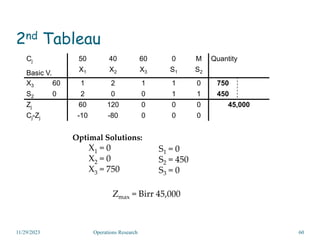
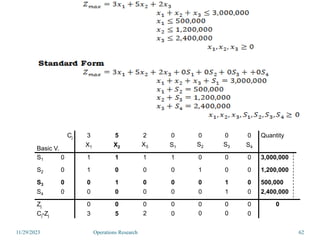
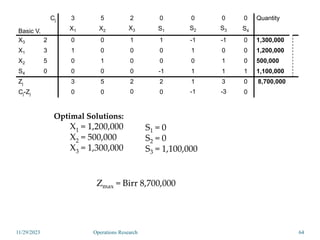
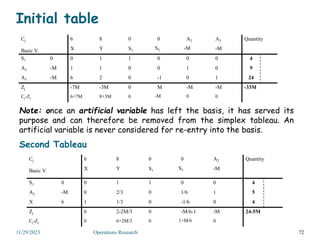
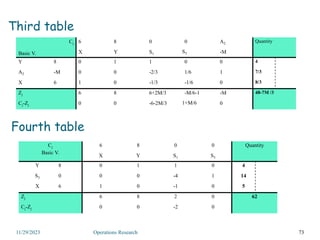
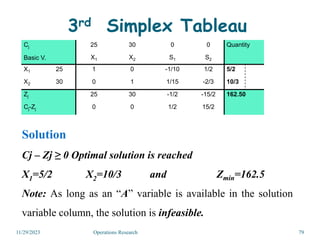
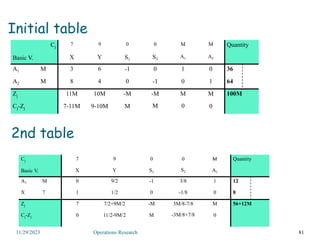
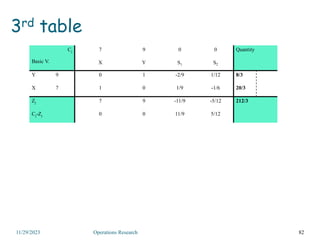
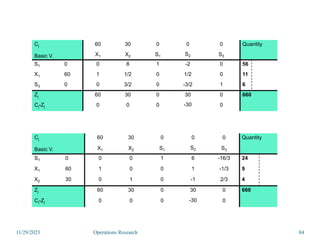
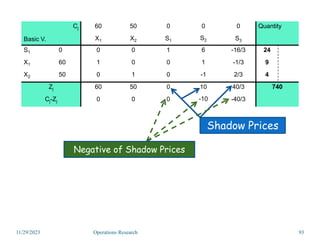
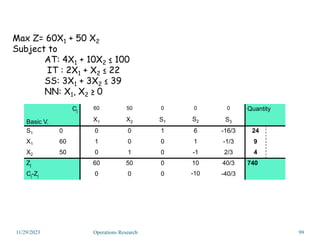
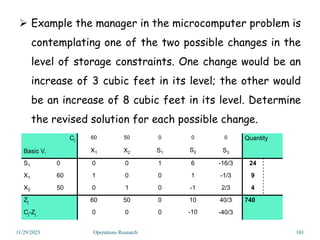
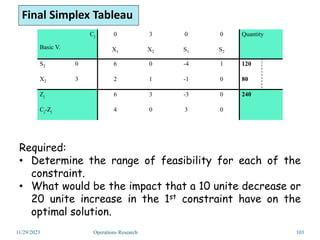
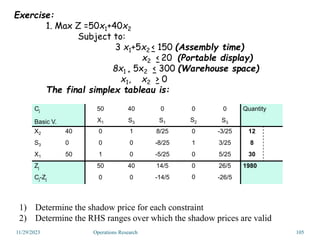
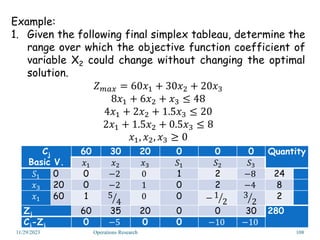
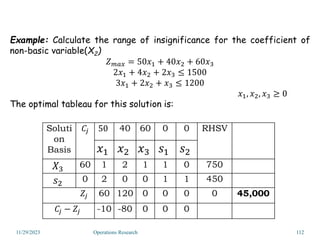
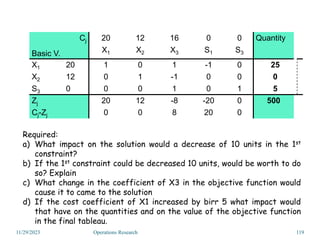
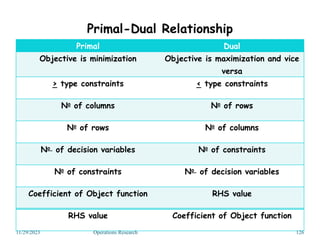
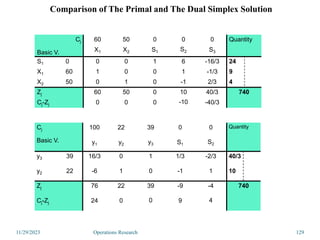
Linear programming is an optimization method that allocates scarce resources in the best way subject to constraints. It can be used to maximize profit, revenue, or minimize costs. A linear programming model specifies an objective function and constraints that are linear relationships. The objective is to find the optimal solution that satisfies all constraints. Graphical and algebraic solution methods can be used to solve linear programming problems. The graphical method plots the constraints and finds the optimal solution at an intersection point.