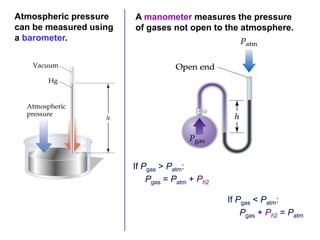
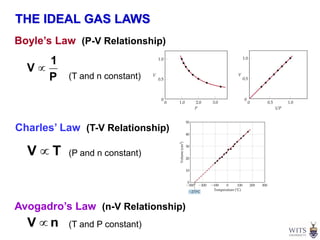
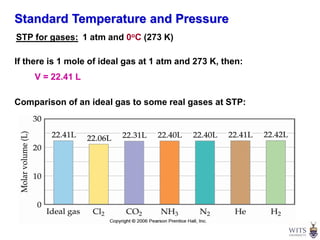
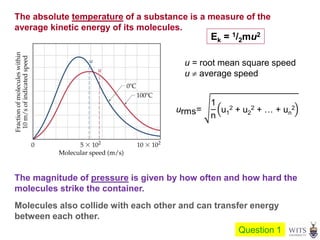
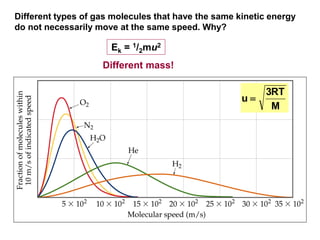
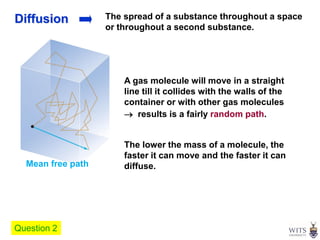
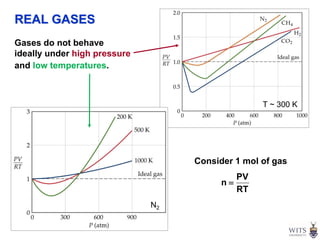
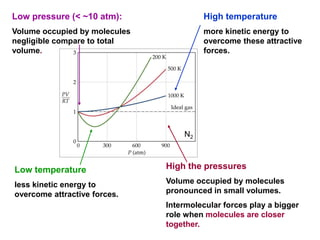
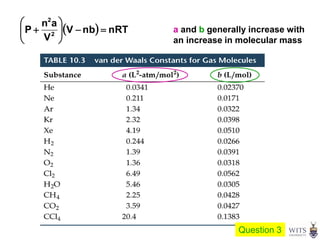
This document discusses gases and gas laws. It begins by defining pressure and discussing atmospheric pressure and how it can be measured. It then covers the three main gas laws (Charles' Law, Boyle's Law, Avogadro's Law) and combines them into the ideal gas equation. The document also discusses gas mixtures and partial pressures, kinetic molecular theory, effusion and diffusion of gases, deviations from ideal behavior at high pressures/low temperatures, and uses the van der Waals equation to account for real gas behavior.

1. GASES
Chapter 10

2. Pressure is the force that acts on a given area.
A
F
P  SI Units: N.m-2 = Pa (Pascal)
Other units:
1 atm = 760 torr = 760 mm Hg = 101.325 kPa
1 bar = 100 kPa
PRESSURE
QUICK RECAP
Atmospheric pressure:
the atmosphere exerts a downward force (due to gravity) and hence
a pressure on the earth’s surface.

3. Atmospheric pressure
can be measured using
a barometer.
A manometer measures the pressure
of gases not open to the atmosphere.
If Pgas > Patm:
Pgas = Patm + Ph2
If Pgas < Patm:
Pgas + Ph2 = Patm

4. Charles’ Law (T-V Relationship)
Boyle’s Law (P-V Relationship)
Avogadro’s Law (n-V Relationship)
(T and n constant)
P
1
V 
(P and n constant)
T
V 
(T and P constant)
n
V 
THE IDEAL GAS LAWS

5. R is the gas constant.
R = 0.08206 L.atm.mol-1.K-1
R = 8.315 m3.Pa.mol-1.K-1
R = 8.315 J.mol-1.K-1
nRT
PV 
If we have a gas under two sets of conditions, then:
nT
PV
R 

2
2
2
2
1
1
1
1
T
n
V
P
T
n
V
P

IDEAL GAS EQUATION

6. Comparison of an ideal gas to some real gases at STP:
STP for gases: 1 atm and 0oC (273 K)
If there is 1 mole of ideal gas at 1 atm and 273 K, then:
V = 22.41 L
Standard Temperature and Pressure

7. Dalton’s Law of Partial Pressures:
In a gas mixture the total pressure is given by the sum of partial
pressures of each component.
Since gas molecules are so far apart, we can assume they behave
independently.




 3
2
1
total P
P
P
P
Each gas in the
mixture obeys the
ideal gas equation:







V
RT
n
P i
i
  









V
RT
n
n
n
P 3
2
1
total 
Gas Mixtures and Partial Pressures
Consider one gas in a mixture of gases:
P1 = n1RT/V
Pt = ntRT/V t
1
t
1
n
n
P
P

 t
t
1
1 P
n
n
P 








  P1 = x1Pt
mole fraction 7

8. To find the amount of gas produced by a reaction
 collect the gas by displacing a volume of water.
water
gas
total P
P
P 

Note: there is water vapour
mixed in with the gas.
To calculate the amount of gas produced, we need to correct for the
partial pressure of the water vapour:
nRT
PV 
E.g. 2KClO3(s)  2KCl(s) + 3O2(g)
Raise or lower container until the water
levels inside and outside are the same.
Ptotal = Patm
Pwater = 0.031atm at 25oC
END OF RECAP

9. Why do gases behave as they do? Look at molecular level.
Assumptions:
• Gases consist of a large number of molecules
in constant random motion.
• The volume of individual molecules is
negligible compared to volume of the
container.
• Intermolecular forces (forces between gas
molecules) are negligible.
• Energy can be transferred between molecules,
but total kinetic energy is constant at constant
temperature.
• Average kinetic energy of molecules is
proportional to temperature.
KINETIC MOLECULAR THEORY

10. The magnitude of pressure is given by how often and how hard the
molecules strike the container.
The absolute temperature of a substance is a measure of the
average kinetic energy of its molecules.
Molecules also collide with each other and can transfer energy
between each other.
Ek = 1/2mu2
u = root mean square speed
u  average speed
u1
2 + u2
2 + … + un
2
Question 1

11. Ek = 1/2mu2
Different types of gas molecules that have the same kinetic energy
do not necessarily move at the same speed. Why?
Different mass!
M
RT
3
u 

12. The escape of gas molecules through a tiny
hole into an evacuated space
The faster molecules move, the greater
the probability that they will effuse.
Effusion
Graham’s Law of Effusion:
Consider two gases under identical PV-conditions with effusion
rates r1 and r2, then:
1
2
2
1
2
1
2
1
M
M
M
RT
3
M
RT
3
u
u
r
r



i.e. rate of effusion is inversely proportional
to the square root of its molar mass.

13. The spread of a substance throughout a space
or throughout a second substance.
A gas molecule will move in a straight
line till it collides with the walls of the
container or with other gas molecules
 results is a fairly random path.
Mean free path
The lower the mass of a molecule, the
faster it can move and the faster it can
diffuse.
Diffusion
Question 2

14. REAL GASES
Gases do not behave
ideally under high pressure
RT
PV
n 
Consider 1 mol of gas
and low temperatures.
T ~ 300 K
N2

15. Why do we see these deviations?
Ideal gas molecules are assumed to occupy no space and have
no intermolecular forces between them.
Real molecules do occupy space.
At high the pressures this becomes more
critical since the amount of open space is
significantly less.
Intermolecular forces play a bigger role when
molecules are closer together (high pressure).
Also at lower temperature, less kinetic energy
to overcome these attractive forces.
If there are stronger the forces of attraction
between the molecules, they will strike the
walls of the container with less force, thus
reducing the pressure.

16. N2
Low temperature
less kinetic energy to
overcome attractive forces.
High the pressures
Volume occupied by molecules
pronounced in small volumes.
Intermolecular forces play a bigger
role when molecules are closer
together.
High temperature
more kinetic energy to
overcome these attractive
forces.
Low pressure (< ~10 atm):
Volume occupied by molecules
negligible compare to total
volume.

17. Corrections for Non-ideal Behaviour
Van der Waals equation for real gases:
Ideal gas:
V
nRT
P 
2
2
V
a
n
nb
V
nRT
P 


Correction for volume
of molecules
Van der Waals constant
b is a measure of the
volume occupied by a
mole of gas molecules.
Unit for b: L mol-1
Correction for molecular attraction
The pressure is reduced by the factor
n2a/V2.
Attractive forces between pairs of
molecules increases as the square of
the number of molecules per unit
volume i.e. (n/V)2.
Van der Waals constant a reflects how
strongly gas molecules attract each
other.
Unit for a: L2 atm mol-2

18.   nRT
nb
V
V
a
n
P 2
2










 a and b generally increase with
an increase in molecular mass
Question 3