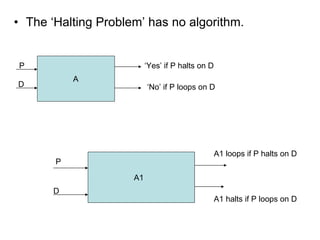
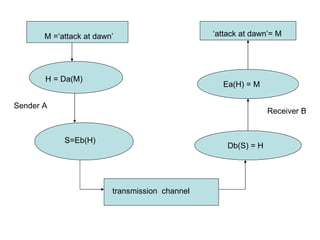
The document discusses key concepts related to algorithms including: 1) An algorithm is a precise method for solving a problem that is applicable to every instance of the problem and terminates in finite time. 2) Some problems like the halting problem have no algorithmic solution and are considered incomputable. 3) Public key cryptography relies on the fact that some problems like integer factorization are considered infeasible, even though their inverse problems are feasible.

1. COMPUTERS & ALGORITHMS C.S.MOGHE

2. Concept of an ‘algorithm’. Algorithms studied in and by themselves. Two characteristics required of an algorithm. Inherent limitations to what is computable. Many problems can never have solutions. ‘ Halting Problem’ a classic that has no solution. Some problems only theoretically solvable. Applications of such intractable problems. PREVIOUS EXPOSURE TO COMPUTERS NOT NEEDED

3. ‘ Algorithm’ a precise specification of the method or procedure to be followed for solving a problem. algorithm recipe input ingredients prog. language natural language computer cook / chef Algorithm, an abstract entity: machine and language independent. For a procedure to be an algorithm, two reqr.: Applicable to every instance of the problem. Terminate/halt and yield an answer in finite time.

4. Prime: An integer that is divisible only by 1 and by itself. Algorithm for checking if number (N >3) is prime: Set k =2. 2. Divide N by k. If remainder = 0 then step 7. 4. Increment k. 5. If k<>N then step 2. 6. Answer ‘Yes’ and stop. 7. Answer ‘No’ and stop. Important : Applicable for every N > 3.

5. Goldbach Conjecture : Every even integer greater than 2 can be expressed as the sum of two primes. Given an integer 2N, number of attempts to find the primes is limited to the value of N. Hence termination of procedure guaranteed . Variation : Every even integer can be expressed as the difference of 2 primes. Since number of primes is infinite, no guarantee of termination! Moral : Not all procedures are algorithms.

6. The ‘Halting Problem’ has no algorithm. A P D ‘ Yes’ if P halts on D ‘ No’ if P loops on D A1 P D A1 loops if P halts on D A1 halts if P loops on D

7. B A1 C loops on P if P halts on D C halts on P if P loops on D C P P P Compare with: ‘This statement is false’. The ‘Halting Problem’ is not decidable. The ‘Equivalence Problem’ is not decidable.

8. While many problems have no algorithms and are therefore unsolvable, many others are only ‘theoretically’ solvable. 22 43 35

9. N cities and ‘cost’ associated with travel between two cities. Problem : Touch every city exactly once so that the total cost is minimum possible. Time required to solve the problem increases dramatically as N increases. For N = 80, for example, the time required is of the order of 500 billion years ! Need therefore for study of ‘time complexity’ of algorithms.

10. 10 5 22 7 8 15 32 2 : n-1 comparisons 2 5 22 7 8 15 32 10 : n-2 comparisons 2 5 22 7 8 15 32 10 : n-3 comparisons . . Hence total number of comparisons is n(n-1)/2 or of the order of n 2 or O(n 2 ). Important : Time complexity estimated without regard to language in which algorithm written, or machine on which executed!

11. Sorting algorithm of O(n 2 ) establishes upper bound on the sorting problem. Inherent complexity of sorting no worse than O(n 2 ). Finding lower bound for an algorithmic problem is not trivial. Lower bound  no better than Inherent complexity of sorting problem no better than O(n log n). Concept of ‘algorithmic gap’.

12. Massive algorithmic gaps may exist for many problems. Polynomial time complexity problems are FEASIBLE / TRACTABLE . Traveling Salesman Algorithm has time complexity of O(N!), but has important applications in Telephone networks IC design and layout Programming of a robot arm Construction scheduling etc ‘ Time Table Problem’ subject to given constraints also infeasible.

13. Limitations due to infeasibility can be turned into a virtue! Cryptography is one such important instance. Conventional private cryptosystems: H = E(M) : D(H) = M Disadvantages of this system: Key transmission on a secure channel. Authentication difficult. Lock and key analogy. Public key cryptography to the rescue!

14. Public key cryptography relies on the crucial fact that ‘Some problems are infeasible (today)’. Padlock analogy: encryption function E is public, decryption function D is private. Functions E and D are mutual inverses: D(E(M)) = M and E(D(M)) = M Moreover and more importantly, (E, D) a trap-door function pair : given E, finding out D is infeasible! However, applying both D and E feasible! Crucially dependent on the fact that: Testing for prime number is feasible. Factorization (a closely related problem) is not!

15. M =‘attack at dawn’ ‘ attack at dawn’= M H = Da(M) S=Eb(H) Db(S) = H Ea(H) = M transmission channel Sender A Receiver B

16. Advantages of Public Key Cryptography: No prior arrangement or passing of keys. Signed message transmission. Later denial by sender not possible. Faking of message not possible. Message modification by receiver not possible. And all of this because: SOME PROBLEMS ARE INFEASIBLE.

17. Concept of ‘algorithm’ and its two characteristics. Study of time complexity of algorithms. Infeasible problems and an application that depends on problem infeasibility! Incomputability or unsolvability. Undecidability of the ‘Halting Problem’. No matter how ‘powerful’ the computer, many problems inherently unsolvable. :Thank You:

18. This talk is based largely on the material available in 'Algorithmics: The Spirit of Computing' by David Harel; Add. Wesley Press.