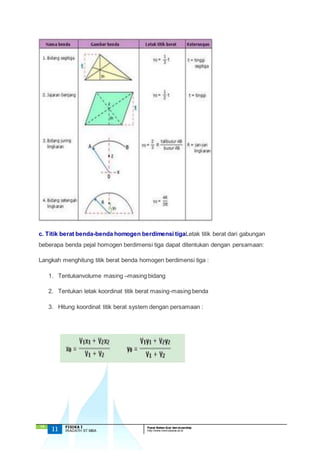
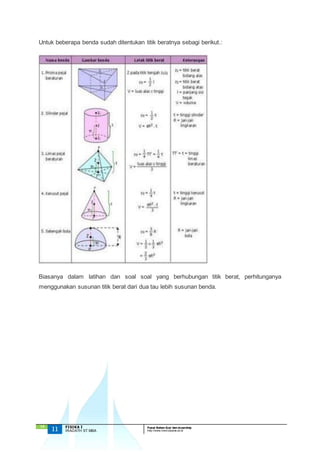
Pusat massa dan titik berat suatu benda merupakan titik tempat berpusatnya massa atau berat benda tersebut. Pusat massa tidak dipengaruhi gravitasi sedangkan titik berat dipengaruhi. Modul ini menjelaskan cara menentukan pusat massa dan titik berat benda homogen satu, dua, dan tiga dimensi dengan rumus dan contohnya.

1. MODUL PERKULIAHAN
Fisika I
Pusat Massa Benda Homogen
Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh
TEKNIK TEKNIK ELEKTRO
11
MK14001 IRADATH ST.MBA
Abstract Kompetensi
Mahasiswa dapat memahami
Dan mengetahui tentang pusat
Massa sebuah benda yang
homogen
1.Mahasiswa dapat memahami tentang
Pusat massa sebuah benda
2.Mahasiswa dapat mengerti tentang
Pusat massa dan titi berat sebuah
benda

2. MODUL XI : MK FISIKA 1 :
DOSEN : IRADATH ST. MBA
Pusat Massa
banyak titik, selain terdapat gaya eksternal (Fe) juga terdapat gaya internal (Fij) antar titik-titik
dalam benda. Untuk itu diperkenalkan pusat massa, di mana gaya aksi yang diberikan ke
setiap titik materi dipandang sama dengan gaya aksi yang diberikan pada pusat massa
suatu sistem materi tunggal. Contoh sederhananya saat kita melempar bola ke atas,
sebenarnya semua titik pada materi mendapatkan gaya aksi yang besarnya kita sebut Fi.
Namun akan lebih sederhana jika kita menganggap bola itu sebagai satu titik materi saja,
yakni pada pusat massanya.
dengan nol. Untuk benda simetris yang homogen, letak pusat massa tentulah berada tepat
di tengah-tengah benda. Lalu, bagaimana untuk benda yang tidak simetris?
Jika kita mengambil suatu titik di mana gaya internalnya nol, diperoleh
Titik itu haruslah mewakili keseluruhan sistem secara makroskopis, sehingga notasi sumasi
di ruas kiri menjadi lenyap. Titik itulah yang kita sebut sebagai pusat massa, yang berjarak R
dari sembarang pemilihan koordinat awal.
`13
Interaksi antar materi seringkali merupakan interaksi banyak titik materi. Pada sistem
Pusat massa suatu benda ialah titik di mana gaya internal pada sistem massa sama
Ambillah persamaan gaya yang bekerja pada sistem banyak titik
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

3. Akhirnya diperoleh
Pendekatannya dapat dilakukan dengan dua cara yaitu diskret dan kontinu. Misal untuk
gambar di bawah ini.
letak pusat massa benda itu? Kita akan menghitungnya bagian-demi bagian dan parameter
demi parameter (x, y, z).
Kubus pertama (kiri)
r1(x,y,z) = (2,2,2)
Kubus ke-dua (tengah)
r2(x,y,z) = (2,6,2)
Kubus ke-tiga (depan)
r3(x,y,z) = (6,6,2)
Kubus ke-empat (atas)
r4(x,y,z) = (2,6,6)
Karena semua kubus kecil memiliki massa yang sama, m, maka pusat massanya, R ialah:
`13
Pada postingan ini akan dibahas cara menentukan pusat massa benda homogen.
Jika kubus-kubus kecil penyusunnya memiliki rusuk 4 cm dan massa m, di manakah
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

4. Akhirnya diperoleh .
Bagaimana dengan pelat berbentuk segitiga siku-siku?
lalu dijumlahkan (jumlahan Riemann). Berbicara tentang penjumlahan Riemann artinya kita
akan bersinggungan dengan integral. Dalam bentuk integral, persamaan pusat massa dapat
dituliskan
Di mana dm ialah elemen massa, atau massa dari tiap-tiap segmen. Di sini kita
mendefinisikan massa jenis σ (massa per satuan luas), yakni σ = M/A. Karena luas segitiga
di atas ialah ½ a.b, maka:
Mengingat segitiga siku-siku dapat kita nyatakan dalam persamaan garis y(x) = mx = bx/a,
`13
Contoh tadi adalah untuk benda yang bisa didekati dengan metode diskret.
Untuk benda semacam ini kita dapat memecahnya menjadi segmen-segmen kecil
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

5. diperoleh luas tiap segmen yang berbentuk segi empat (dA) tidak lain adalah dx × y(x)
sehingga elemen massa
Sekarang kita sudah bisa memulai menghitung pusat massa segitiga.
Substitusi kembali M = σab/2, akhirnya diperoleh
mencari sendiri nilai Ry. Caranya serupa, hanya saja Anda harus mengubah fungsinya
menjadi x(y) = ay/b dan integrasikan terhadap y, nanti akan diperoleh bentuk
Pada akhirnya pusat massanya ialah
`13
Akhirnya ketemu juga, tapi itu baru absisnya, belum ordinatnya. Silakan Anda
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

6. STATIKA adalah ilmu kesetimbangan yang menyelidiki syarat-syarat gaya yang bekerja
pada sebuah benda/titik materi agar benda/titik materi tersebut setimbang.
PUSAT MASSA DAN TITIK BERAT
Pusat massa dan titik berat suatu benda memiliki pengertian yang sama, yaitu suatu titik
tempat berpusatnya massa/berat dari benda tersebut. Perbedaannya adalah letak pusat
massa suatu benda tidak dipengaruhi oleh medan gravitasi, sehingga letaknya tidak selalu
berhimpit dengan letak titik beratnya.
1. PUSAT MASSA
Koordinat pusat massa dari benda-benda diskrit, dengan massa masing-masing M1,
M2,....... , Mi ; yang terletak pada koordinat (x1,y1), (x2,y2),........, (xi,yi) adalah:
X = (å Mi . Xi)/(Mi)
Y = (å Mi . Yi)/(Mi)
2. TITIK BERAT (X,Y)
Koordinat titik berat suatu sistem benda dengan berat masing-masing W1, W2, ........., Wi ;
yang terletak pada koordinat (x1,y1), (x2,y2), ............, (xi,yi) adalah:
X = (å Wi . Xi)/(Wi)
Y = (å Wi . Yi)/(Wi)
LETAK/POSISI TITIK BERAT
1. Terletak pada perpotongan diagonal ruang untuk benda homogen berbentuk teratur.
2. Terletak pada perpotongan kedua garis vertikal untuk benda sembarang.
3. Bisa terletak di dalam atau diluar bendanya tergantung pada homogenitas dan bentuknya.
TITIK BERAT BEBERAPA BENDA
Garis lurus
yo = 1/2 AB
z = di tengah-tengah AB
`13
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

7. Busur lingkaran
yo = AB/AB .
AB = tali busur
AB = busur AB
R = jari-jari lingkaran
Busur setengah lingkaran
yo = 2.R/p
R = jari-jari lingkaran
Juring lingkaran
yo = AB/AB.2/3.R
AB = tali busur
AB = busur AB
R = jari-jari lingkaran
Setengah lingkaran
yo = 4.R/3 p
R = jari-jari lingkaran
Selimut setengah bola
yo = 1/2 R
R = jari-jari lingkaran
Selimut limas
yo = 1/3 t
t = tinggi limas
Selimut kerucut
yo = 1/3 t
t = tinggi kerucut
Setengah bola
yo = 3/8 R
R = jari-jari bola
Limas
yo = 1/4 t
t = tinggi limas
Kerucut
yo = 1/4 t
t = tinggi kerucut
Cat. : Dalam menyelesaikan persoalan titik berat benda, terlebih dahulu bendanya dibagi-bagi
kemudian baru diselesaikan dengan rumusan yang ada.
`13
sesuai dengan bentuk benda khusus yang sudah diketahui letak titik beratnya
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

8. PUSAT MASSA DAN TITIK BERAT
Pusat massa dan titik berat suatu benda memiliki pengertian yang sama, yaitu suatu titik
tempat berpusatnya massa/berat dari benda tersebut. Perbedaannya adalah letak pusat
massa suatu benda tidak dipengaruhi olehmedan gravitasi, sehingga letaknya tidak selalu
berhimpit dengan letak titik beratnya.
a. Titik berat benda homogen satu dimensi (garis)
Untuk benda-benda berbentuk memanjang seperti kawat , massa benda dianggap diwakili
oleh panjangnya (satu dimensi) dan titik beratnya dapat dinyatakan dengan persamaan
berikut:
Langkah penentuan titik berat benda homogen 1 dimensi :
b. Titik berat benda-benda homogen berbentuk luasan (dua dimensi)
Jika tebal diabaikan maka benda dapat dianggap berbentuk luasan (dua dimensi), dan titik
berat gabungan benda homogen berbentuk luasan dapat ditentukan dengan persamaan
berikut:
Langkah menghitung Titik Berat Homogen Berbentuk Luasan (dua Dimensi ) :
1. Tentukan Luas masing-masing bidang
2. Tentukan letak titik berat masing-masing benda
3. Tentukan Koordinat titik berat bidang dengan menggunakan persamaan :L
Titik berat benda homogen berbentuk luasan yang bentuknya teratur terletak pada sumbu
simetrinya. Untuk bidang segi empat, titik berat diperpotongan diagonalnya, dan untuk
lingkaran terletak dipusat lingkaran. Titik berat bidang homegen di perlihatkan pada tabel
berikut:
`13
1. Tentukan panjang masing-masing benda
2. Tentukan letak titik berat masing-masing benda
3. Hitung koordinat titik berat berat benda dengan persamaan
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

9. c. Titik berat benda-benda homogen berdimensi tigaLetak titik berat dari gabungan
beberapa benda pejal homogen berdimensi tiga dapat ditentukan dengan persamaan:
Langkah menghitung titik berat benda homogen berdimensi tiga :
`13
1. Tentukanvolume masing –masing bidang
2. Tentukan letak koordinat titik berat masing-masing benda
3. Hitung koordinat titik berat system dengan persamaan :
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id

10. Untuk beberapa benda sudah ditentukan titik beratnya sebagi berikut.:
Biasanya dalam latihan dan soal soal yang berhubungan titik berat, perhitunganya
menggunakan susunan titik berat dari dua tau lebih susunan benda.
`13
11 FISIKA I Pusat Bahan Ajar dan eLearning
IRADATH ST.MBA http://www.mercubuana.ac.id