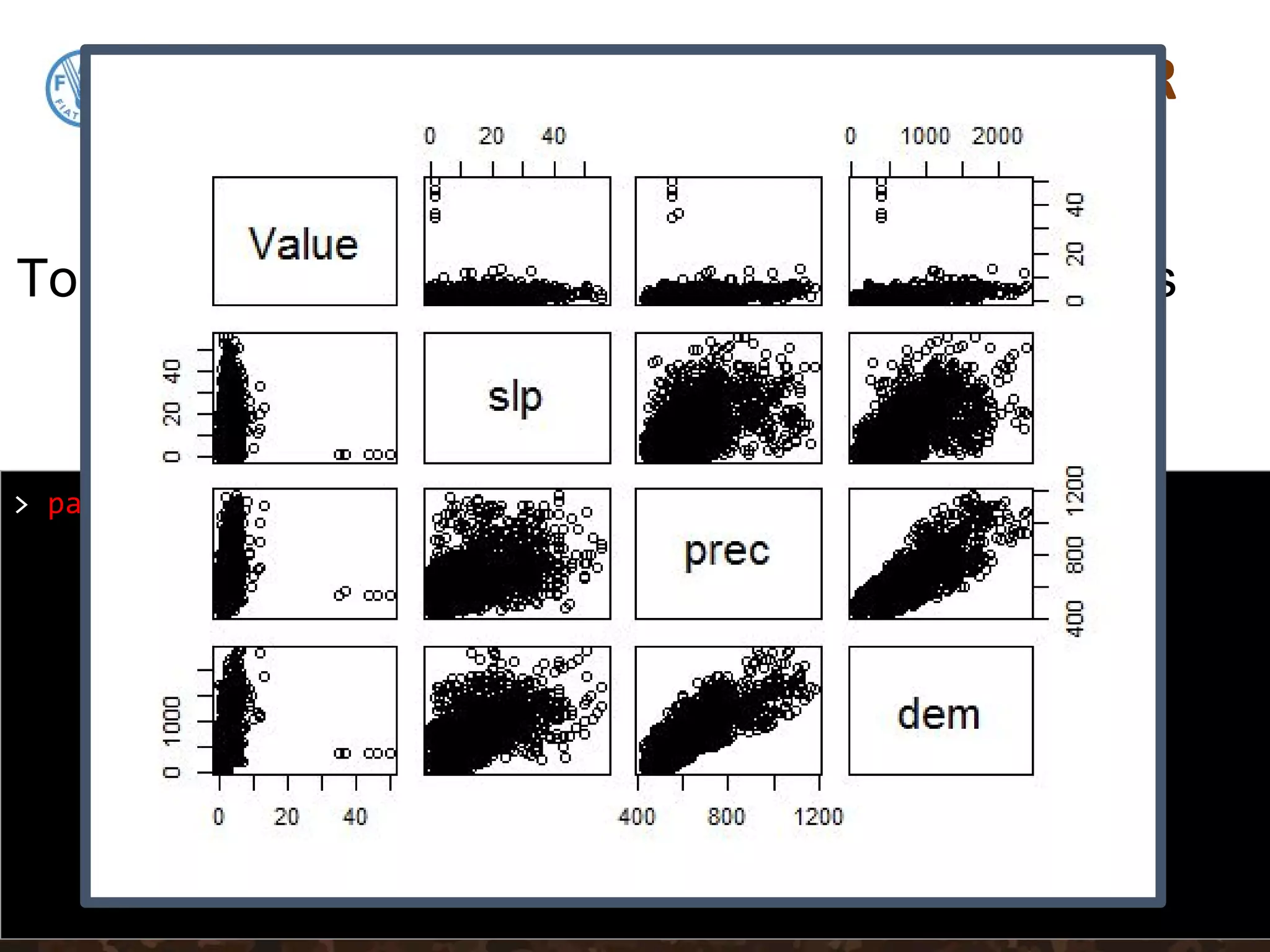
Simple linear regression uses a single independent variable to predict the value of a dependent variable. Multiple linear regression extends this to use multiple independent variables to predict the dependent variable. The document demonstrates multiple linear regression in R by regressing soil organic carbon (SOC) on elevation, precipitation, and slope using the lm() function. This produces a model object that contains coefficients, residuals, fitted values and other details about the regression model.

4. Simple linear regression uses a independent variable
to predict the outcome of a dependent variable. This
is the most basic form of regression, numerous
complex modeling techniques can be learned by
understanding this basic complex.

5. In R several classical statistical models can be
implemented using the function: lm (linear model).
The lm function can be used for simple and multiple
linear regression
> ?lm

6. In R several classical statistical models can be
implemented using the function: lm (linear model).
The lm function can be used for simple and multiple
linear regression
> ?lm
Usage
lm(formula, data, subset, weights, na.action,
method = "qr", model = TRUE, x = FALSE, y = FALSE,
qr = TRUE, singular.ok = TRUE, contrasts = NULL,
offset, ...)

7. The first argument in the lm function (formula) is
where you specify the structure of the statistical
model.
Common structure of a statistical model is:
y ~x Simple linear regression of y on x
y ~ x + z Multiple regression of y on x and z
>
https://drive.google.com/file/d/0B4-nNA2Ua3DoUmJMQ3JJTFpzTDg/view?usp=sharing

8. To demonstrate simple linear regression in R, we will
again use the Macedonian Soil Dataset. Here we will
regress Soil Organic Carbon on DEM.
DSM_table <- read.csv("DSM_table2.csv")

9. To demonstrate simple linear regression in R, we will
again use the Macedonian Soil Dataset. Here we will
regress Soil Organic Carbon on DEM.
> head(DSM_table2)
ID ProfID X Y UpperDepth LowerDepth Value Lambda
1 4 P0004 7485085 4653725 0 30 11.878804 0.1
2 7 P0007 7486492 4653203 0 30 3.490205 0.1
3 8 P0008 7485564 4656242 0 30 2.317673 0.1
4 9 P0009 7495075 4652933 0 30 1.936148 0.1
5 10 P0010 7494798 4651945 0 30 1.339719 0.1
6 11 P0011 7492500 4651760 0 30 2.285384 0.1
tsme slp prec dem
1 0.160096433 13 998.034 2327
2 0.002569598 35 1014.300 1986
3 0.002601836 6 779.994 1243
4 0.002841078 25 839.183 1120
5 0.002677120 30 843.919 1098

10. The summary statistics,
> summary(cbind(SOC = DSM_table$Value, Slope =DSM_table2$slp,
Precipitation=DSM_table2$prec, DEM=DSM_table$dem))
SOC Slope Precipitation DEM
Min. : 0.000 Min. : 0.000 Min. : 424.5 Min. : 45.0
1st Qu.: 1.005 1st Qu.: 0.000 1st Qu.: 532.3 1st Qu.: 404.2
Median : 1.493 Median : 3.000 Median : 564.3 Median : 592.0
Mean : 1.912 Mean : 7.414 Mean : 597.5 Mean : 642.3
3rd Qu.: 2.244 3rd Qu.:11.000 3rd Qu.: 641.8 3rd Qu.: 768.0
Max. :50.332 Max. :56.000 Max. :1180.3 Max. :2375.0
NA's :1

11. Our hypothesis here is that elevation is a good
predictor of SOC!?.To start, let’s have a look at what
the data looks like
plot(DSM_table$Value, DSM_table$dem)

12. Our hypothesis here is that elevation is a good
predictor of SOC!?.To start, let’s have a look at what
the data looks like
plot(DSM_table$Value, DSM_table$dem)

13. There appears there is not meaningful. To fit a linear
model, we can use the lm function:
model1 <- lm(Value ~ dem, data=DSM_table, y=TRUE, x = TRUE)
> model1
Call:
lm(formula = Value ~ dem, data = DSM_table, x = TRUE, y = TRUE)
Coefficients:
(Intercept) dem1
0.715117 0.001856

14. > summary(model1)
Call:
lm(formula = Value ~ dem1, data = DSM_table, x = TRUE, y = TRUE)
Residuals:
Min 1Q Median 3Q Max
-3.917 -0.769 -0.224 0.389 48.895
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.151e-01 6.929e-02 10.32 <2e-16 ***
dem1 1.856e-03 9.367e-05 19.82 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.954 on 3300 degrees of freedom
Multiple R-squared: 0.1063, Adjusted R-squared: 0.1061
F-statistic: 392.6 on 1 and 3300 DF, p-value: < 2.2e-16

15. > class(model1)
[1] "lm"
the output from the lm function is an object of class
lm. An object of class "lm" is a list containing at least
the following components:

16. > class(model1)
[1] "lm"
the output from the lm function is an object of class
lm. An object of class "lm" is a list containing at least
the following components:
coefficients - a named vector of coefficients
residuals - the residuals, that is response minus fitted values.
fitted.values - the fitted mean values.
rank - the numeric rank of the fitted linear model.
weights - (only for weighted fits) the specified weights.
df.residual -the residual degrees of freedom.
call - the matched call.
terms - the terms object used.
contrasts - (only where relevant) the contrasts used.
xlevels -(only where relevant) a record of the levels of the factors
used in fitting.
offset- the offset used (missing if none were used).
y - if requested, the response used.
x- if requested, the model matrix used.
model - if requested (the default), the model frame used.
na.action - (where relevant) information returned by model.frame on
the special handling of NAs.

17. class(model1)
[1] "lm"
model1$coefficients
(Intercept) dem1
0.715116901 0.001856089
> formula(model1)
Value ~ dem1
the output from the lm function is an object of class
lm. An object of class "lm" is a list containing at least
the following components:

18. head(residuals(model1))
1 2 3 4 5 6
6.8445691 -1.2674728 -0.7045624 -0.5960802 -1.1628119 -1.1990168
names(summary(model1))
[1] "call" "terms" "residuals" "coefficients"
[5] "aliased" "sigma" "df" "r.squared"
[9] "adj.r.squared" "fstatistic" "cov.unscaled"
Here is a list of what is available from the summary
function for this model:

19. summary(model1)[[4]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.715116901 6.928677e-02 10.32112 1.333183e-24
dem1 0.001856089 9.367314e-05 19.81452 1.188533e-82
summary(model1)[[7]]
[1] 2 3300 2
To extract some of the information from the
summary which is of a list structure, we can use:

20. > summary(model1)[["r.squared"]]
[1] 0.1063245
> summary(model1)[[8]]
[1] 0.1063245
What is the RSquared of model1?

21. > summary(model1)[["r.squared"]]
[1] 0.1063245
> summary(model1)[[8]]
[1] 0.1063245
What is the RSquared of model1?

22. head(predict(model1))
1 2 3 4 5 6
5.034235 4.757678 3.022235 2.532228 2.502530 3.484401
head(DSM_table$Value)
[1] 11.878804 3.490205 2.317673 1.936148 1.339719 2.285384
head(residuals(model1))
1 2 3 4 5 6
6.8445691 -1.2674728 -0.7045624 -0.5960802 -1.1628119 -1.1990168
head(model2$residuals)
1 2 3 4 5 6
7.3395541 -1.1690560 -0.5363049 -1.2854938 -1.9692882 -1.5173124
> head(model2$fitted.values)
1 2 3 4 5 6
4.539250 4.659261 2.853978 3.221641 3.309007 3.802697

23. plot(model1$y, model1$fitted.values)
Lets plot() the observed vs. predicted from
the model

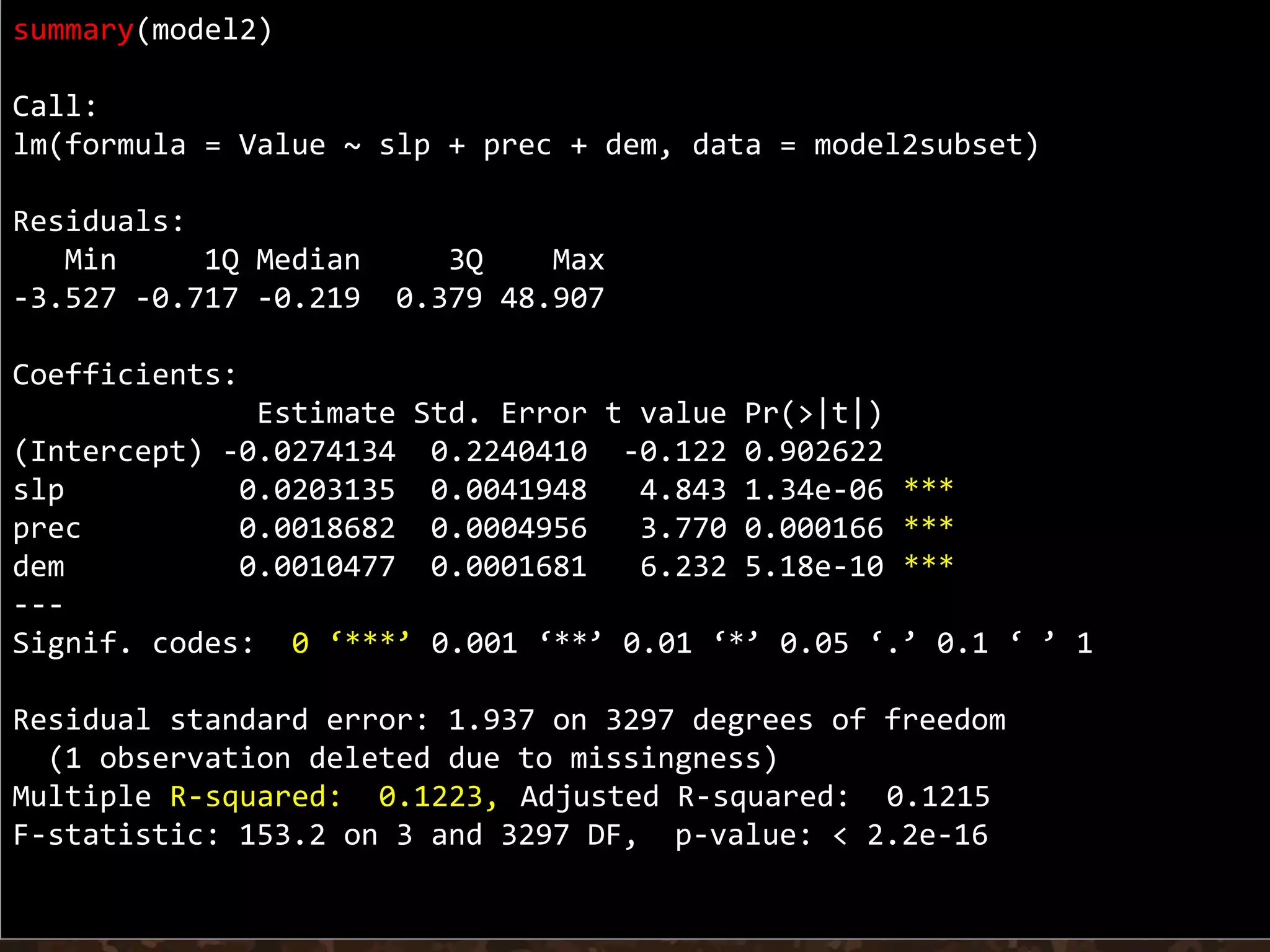
24. model2subset <-DSM_table2[, c("Value", "slp", "prec", "dem")]
summary(model2subset)
Value slp prec dem
Min. : 0.000 Min. : 0.000 Min. : 424.5 Min. : 45.0
1st Qu.: 1.005 1st Qu.: 0.000 1st Qu.: 532.3 1st Qu.: 404.2
Median : 1.493 Median : 3.000 Median : 564.3 Median : 592.0
Mean : 1.912 Mean : 7.414 Mean : 597.5 Mean : 642.3
3rd Qu.: 2.244 3rd Qu.:11.000 3rd Qu.: 641.8 3rd Qu.: 768.0
Max. :50.332 Max. :56.000 Max. :1180.3 Max. :2375.0
NA's :1
We will regress SOC on Precipitation,
Slope and Elevation. First lets subset these
data out, then get their summary statistics

25. cor(na.omit(model2subset))
Value slp prec dem
Value 1.0000000 0.2730310 0.3155474 0.3317814
slp 0.2730310 1.0000000 0.5765489 0.6011170
prec 0.3155474 0.5765489 1.0000000 0.8158338
dem 0.3317814 0.6011170 0.8158338 1.0000000
A quick way to look for relationships between
variables in a data frame is with the cor function.
Note the use of the na.omit function.

26. > pairs(na.omit(model2subset))
To visualize these relationships, we can use pairs

27. > pairs(na.omit(model2subset))
To visualize these relationships, we can use pairs

28. model2 <- lm(Value ~ slp + prec + dem, data = model2subset)
model2
Call:
lm(formula = Value ~ slp + prec + dem, data = model2subset)
Coefficients:
(Intercept) slp prec dem
-0.027413 0.020314 0.001868 0.001048
fitting the multiple linear regression,

29. summary(model2)
Call:
lm(formula = Value ~ slp + prec + dem, data = model2subset)
Residuals:
Min 1Q Median 3Q Max
-3.527 -0.717 -0.219 0.379 48.907
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0274134 0.2240410 -0.122 0.902622
slp 0.0203135 0.0041948 4.843 1.34e-06 ***
prec 0.0018682 0.0004956 3.770 0.000166 ***
dem 0.0010477 0.0001681 6.232 5.18e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.937 on 3297 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.1223, Adjusted R-squared: 0.1215
F-statistic: 153.2 on 3 and 3297 DF, p-value: < 2.2e-16

30. TASK1:
Regress SOC (Value) on; Slope (slp), Elevation (dem), TWI
(twi), Annual Nightly Mean Temperature (tmpn), Annual Daily
Mean Temperature (tmpd)
TASK2: Share you results here,
https://goo.gl/zlNcb5
Sample Data Sheet
https://goo.gl/g5NQCv

31. TASK1:
Regress SOC (Value) on; Slope (slp), Elevation (dem), TWI
(twi), Annual Nightly Mean Temperature (tmpn), Annual Daily
Mean Temperature (tmpd)
TASK2: Share your results here,
https://goo.gl/zlNcb5
Sample Data
https://goo.gl/g5NQCv