Download to read offline
Uploaded byYandex
002умнов
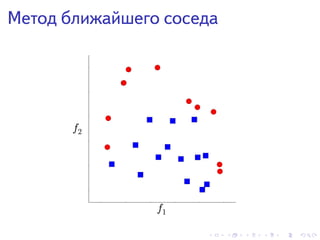
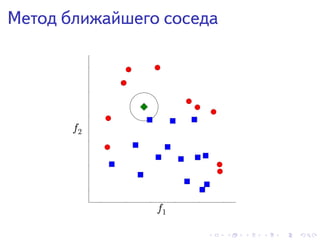
Документ рассматривает использование машинного обучения в различных задачах, таких как фильтрация спама и медицинская диагностика, подчеркивая необходимость обработки больших объемов данных. Обсуждается математика и алгоритмы, стоящие за машинным обучением, включая линейную регрессию и метод ближайшего соседа. Также охватываются аспекты ранжирования страниц на основе релевантности запросов пользователей.
More Related Content
002умнов
- 1. . . .. . . Машинное обучение в Поиске и других задачах Умнов Алексей
- 2. . . .. . . Введение
- 3. . . .. . . Поиск в интернете
- 4. . . .. . . Поиск в интернете .......... мама . рама . мыть . мыть
- 5. . . .. . . Ранжирование .........
- 6. . . .. . . Примеры задач машинного обучения
- 7. . . .. . . Фильтрация спама
- 8. . . .. . . Фильтрация спама Дано: Электронное письмо
- 9. . . .. . . Фильтрация спама Дано: Электронное письмо Адрес отправителя Тема письма Текст письма Файлы письма
- 10. . . .. . . Фильтрация спама Дано: Электронное письмо Адрес отправителя Тема письма Текст письма Файлы письма Необходимо: Определить, является ли данное письмо спамом.
- 11. . . .. . . Медицинская диагностика
- 12. . . .. . . Медицинская диагностика Дано: Пациент
- 13. . . .. . . Медицинская диагностика Дано: Пациент Общие данные пол, возраст Результаты обследований температура, пульс Симптомы наличие головной боли
- 14. . . .. . . Медицинская диагностика Дано: Пациент Общие данные пол, возраст Результаты обследований температура, пульс Симптомы наличие головной боли Необходимо: Определить, болен ли пациент болезнью X.
- 15. . . .. . . Особенности задач Что общего у этих задач? Существует «скрытый» алгоритм их решения.
- 16. . . .. . . Особенности задач Что общего у этих задач? Существует «скрытый» алгоритм их решения. Человека можно научить их решать
- 17. . . .. . . Особенности задач Что общего у этих задач? Существует «скрытый» алгоритм их решения. Человека можно научить их решать Алгоритм решения невозможно строго сформулировать
- 18. . . .. . . Особенности задач Необходимо решать задачу в больших объемах
- 19. . . .. . . Особенности задач Необходимо решать задачу в больших объемах Человек решает задачу медленно
- 20. . . .. . . Особенности задач Необходимо решать задачу в больших объемах Человек решает задачу медленно Нужно использовать машины
- 21. . . .. . . Особенности задач Необходимо решать задачу в больших объемах Человек решает задачу медленно Нужно использовать машины Алгоритма решения нет
- 22. . . .. . . Особенности задач Необходимо решать задачу в больших объемах Человек решает задачу медленно Нужно использовать машины Алгоритма решения нет Есть примеры решения
- 23. . . .. . . Особенности задач Необходимо решать задачу в больших объемах Человек решает задачу медленно Нужно использовать машины Алгоритма решения нет Есть примеры решения Машинное обучение — «обучение» программ на примерах.
- 24. . . .. . . Задача машинного обучения
- 25. . . .. . . Математическая формулировка X — множество объектов, Y — множество ответов.
- 26. . . .. . . Математическая формулировка X — множество объектов, Y — множество ответов. a∗ : X → Y — неизвестный алгоритм.
- 27. . . .. . . Математическая формулировка X — множество объектов, Y — множество ответов. a∗ : X → Y — неизвестный алгоритм. Обучающая выборка T = {xi, yi}l i=1, где yi = a∗ (xi) — множество объектов и известных на них ответов
- 28. . . .. . . Математическая формулировка X — множество объектов, Y — множество ответов. a∗ : X → Y — неизвестный алгоритм. Обучающая выборка T = {xi, yi}l i=1, где yi = a∗ (xi) — множество объектов и известных на них ответов Задача обучения — по выборке T построить алгоритм a : X → Y, который бы как можно лучше приближал a∗
- 29. . . .. . . Математическая формулировка Признаки объектов Признак — численная характеристика объекта Отображение f : X → Df. Df — пространство значений.
- 30. . . .. . . Математическая формулировка Признаки объектов Признак — численная характеристика объекта Отображение f : X → Df. Df — пространство значений. Примеры Df: Df = {0, 1} — бинарный признак. «есть ли в тексте письма слово “банк”», «наблюдается ли у пациента жар». Df = R — количественный признак. Длина письма, возраст пациента.
- 31. . . .. . . Математическая формулировка Построение признаков не входит в задачу машинного обучения.
- 32. . . .. . . Математическая формулировка Построение признаков не входит в задачу машинного обучения. Машинное обучение: построение алгоритма a по обучающей выборке T и признакам объектов f1, . . . , fn.
- 33. . . .. . . Математическая формулировка Построение признаков не входит в задачу машинного обучения. Машинное обучение: построение алгоритма a по обучающей выборке T и признакам объектов f1, . . . , fn. Матрица признаков обучающей выборки F = fi(xj) i=1,...,n j=1,...,l = f1(x1) . . . fn(x1) . . . . . . . . . f1(xl) . . . fn(xl) ( f1(x), . . . , fn(x) ) — вектор признаков объекта
- 34. . . .. . . Стадии машинного обучения Обучение Построение алгоритма a по обучающей выборке. Применение Использование алгоритма a для получения ответов на неизвестных объектах.
- 35. . . .. . . Примеры методов машинного обучения
- 36. . . .. . . Для простоты будем считать, что Y = R Dfi = R для всех i
- 37. . . .. . . Линейная регрессия Рассматриваем линейные комбинации признаков a(α, x) = n∑ i=1 αifi(x), α = (α1, . . . , αn) — неизвестные коэффициенты.
- 38. . . .. . . Линейная регрессия Рассматриваем линейные комбинации признаков a(α, x) = n∑ i=1 αifi(x), α = (α1, . . . , αn) — неизвестные коэффициенты. Минимизация квадратичной ошибки Q(α) = l∑ j=1 a(α, xj) − yj 2 Q(α) → min α
- 39. . . .. . . Линейная регрессия В матричной форме F = f1(x1) . . . fn(x1) . . . . . . . . . f1(xl) . . . fn(xl) Q(α) = Fα − y 2
- 40. . . .. . . Линейная регрессия В матричной форме F = f1(x1) . . . fn(x1) . . . . . . . . . f1(xl) . . . fn(xl) Q(α) = Fα − y 2 Минимизируем ∂Q ∂α = 2FT (Fα − y) = 0 ˆα = ( FT F )−1 FT y
- 41. . . .. . . Линейная регрессия X Y
- 42. . . .. . . Линейная регрессия X Y
- 43. . . .. . . Линейная регрессия Общая схема Обучение Вычисление коэффициентов ˆα = ( FT F )−1 FT y Применение a(ˆα, x) = n∑ i=1 αifi(x)
- 44. . . .. . . Метод ближайшего соседа Метрика на объектах ρ : X × X → R Например евклидово расстояние между векторами признаков ρ(x, y) = n∑ i=1 ( fi(x) − fi(y) )2 1 2
- 45. . . .. . . Метод ближайшего соседа a(x) = yk, где k = argmin j=1,...,l ρ(xj, x) xk — «ближайший сосед», yk — известный ответ на нем.
- 46. . . .. . . Метод ближайшего соседа f1 f2
- 47. . . .. . . Метод ближайшего соседа f1 f2
- 48. . . .. . . Метод ближайшего соседа f1 f2
- 49. . . .. . . Метод ближайшего соседа Общая схема Обучение Запомнить всю обучающую выборку. Применение Для данного x найти ближайшего соседа xk в обучающей выборке и выдать в качестве ответа yk.
- 50. . . .. . . Машинное обучение и ранжирование
- 51. . . .. . . Ранжирование страниц Дано: Запрос пользователя Список результатов
- 52. . . .. . . Ранжирование страниц Дано: Запрос пользователя Список результатов Необходимо: Упорядочить страницы
- 53. . . .. . . Ранжирование страниц Дано: Запрос пользователя Список результатов Необходимо: Упорядочить страницы …в соответствии с их релевантностью
- 54. . . .. . . Ранжирование страниц Дано: Запрос пользователя Список результатов Необходимо: Упорядочить страницы …в соответствии с их релевантностью релевантность (запрос, результат)
- 55. . . .. . . Оценка релевантности Численные методы — Большая Советская Энциклопедия Отлично Математический анализ — Википедия Плохо Реферат: Численные методы линейной алгебры Нормально
- 56. . . .. . . Ранжирование страниц Объекты — пары (запрос, страница) Обучающая выборка — оценка релевантности с помощью ассессоров
- 57. . . .. . . Ранжирование страниц Объекты — пары (запрос, страница) Обучающая выборка — оценка релевантности с помощью ассессоров Признаки Текстовые Пользовательские Статические
- 58. . . .. . . Ранжирование страниц Объекты — пары (запрос, страница) Обучающая выборка — оценка релевантности с помощью ассессоров Признаки Текстовые Пользовательские Статические Предсказание релевантности.
- 59. . . .. . . Конец Вопросы? Дополнительные материалы 1. Сайт www.MachineLearning.ru К. В. Воронцов. Машинное обучение, курс лекций. 2. К. Маннинг, П. Рагван, Х. Шютце. Введение в информационный поиск.