Embed presentation
Download as PDF, PPTX



![4
Pr[✓|x] =
Pr[x|✓] Pr[✓]
P
✓ Pr[x|✓] Pr[✓]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-4-320.jpg)

![8
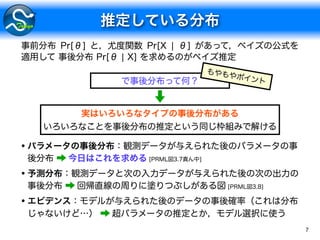
Pr[ θ, Z, D ]
Pr[ θ | D ]
Z D](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-8-320.jpg)
![9
X
y2Dom(Y )
Pr[X, y] = Pr[X]
X
y2Dom(Y )
Pr[y|X] = Pr[X] ⇥ 1
+ =](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-9-320.jpg)
![10
Pr[✓, D] = Pr[✓|D] Pr[D] Pr[✓|D] =
Pr[✓, D]
Pr[D]
D
Z D
D
Pr[✓|D] =
Pr[✓, D]
Pr[D]
=
Pr[✓, D]
P
✓ Pr[✓, D]
=
Pr[D|✓] Pr[✓]
P
✓ Pr[D|✓] Pr[✓]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-10-320.jpg)


![14
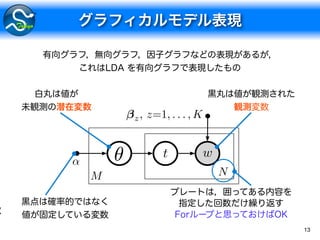
1. N Poisson(ξ)
2. θ Dirichlet(θ ; α)
3. For n in 1 … N
(a) zn Categorical(zn | θ)
(b) wn Categorical(wn | zn; β)
✤
Pr[w, z, ✓; ↵, ] = Pr[✓|↵]
NY
n=1
Pr[zn|✓] Pr[wn|zn, zn ]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-14-320.jpg)


![17
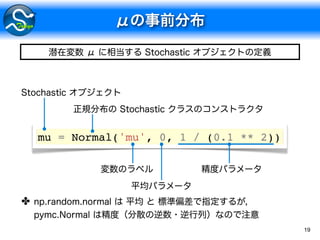
1. μ Normal(0.0, 0.12)
2. For i in 1 … N
(a) xi Normal(μ, 1.02)
μ x
N
• x
• μ
Pr[µ|x1, . . . , xN ] = Pr[µ|{x}]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-17-320.jpg)

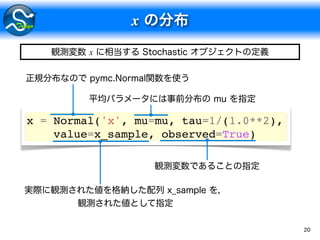
![21
M = MCMC(input=[mu, x])
M.sample(iter=10000)
✤](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-21-320.jpg)
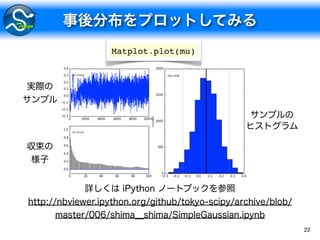
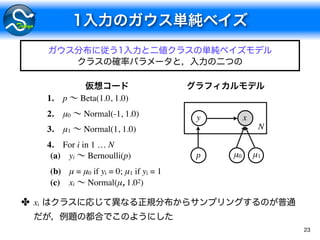
![24
@deterministic(plot=False)
def mu(y=y, mu0=mu0, mu1=mu1):
out = np.empty_like(y, dtype=np.float)
out[y == 0] = mu0
out[y == 1] = mu1
return out](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-24-320.jpg)



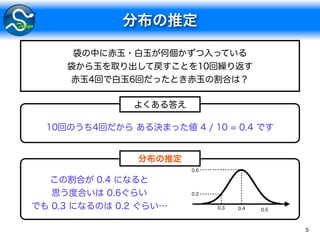
The document outlines a probabilistic framework involving various statistical models, including Poisson and Dirichlet processes, for data generation and inference. It details categorical distributions and MCMC sampling methods for estimating parameters like mean (μ) and weight variables (w). Additionally, it presents the usage of normal distributions for observed data and integrates deterministic functions for specific outcomes based on conditions.



![4
Pr[✓|x] =
Pr[x|✓] Pr[✓]
P
✓ Pr[x|✓] Pr[✓]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-4-320.jpg)



![8
Pr[ θ, Z, D ]
Pr[ θ | D ]
Z D](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-8-320.jpg)
![9
X
y2Dom(Y )
Pr[X, y] = Pr[X]
X
y2Dom(Y )
Pr[y|X] = Pr[X] ⇥ 1
+ =](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-9-320.jpg)
![10
Pr[✓, D] = Pr[✓|D] Pr[D] Pr[✓|D] =
Pr[✓, D]
Pr[D]
D
Z D
D
Pr[✓|D] =
Pr[✓, D]
Pr[D]
=
Pr[✓, D]
P
✓ Pr[✓, D]
=
Pr[D|✓] Pr[✓]
P
✓ Pr[D|✓] Pr[✓]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-10-320.jpg)



![14
1. N Poisson(ξ)
2. θ Dirichlet(θ ; α)
3. For n in 1 … N
(a) zn Categorical(zn | θ)
(b) wn Categorical(wn | zn; β)
✤
Pr[w, z, ✓; ↵, ] = Pr[✓|↵]
NY
n=1
Pr[zn|✓] Pr[wn|zn, zn ]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-14-320.jpg)


![17
1. μ Normal(0.0, 0.12)
2. For i in 1 … N
(a) xi Normal(μ, 1.02)
μ x
N
• x
• μ
Pr[µ|x1, . . . , xN ] = Pr[µ|{x}]](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-17-320.jpg)



![21
M = MCMC(input=[mu, x])
M.sample(iter=10000)
✤](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-21-320.jpg)


![24
@deterministic(plot=False)
def mu(y=y, mu0=mu0, mu1=mu1):
out = np.empty_like(y, dtype=np.float)
out[y == 0] = mu0
out[y == 1] = mu1
return out](https://image.slidesharecdn.com/2014-m-tokyoscipy6-140801092607-phpapp02/85/PyMC-24-320.jpg)

