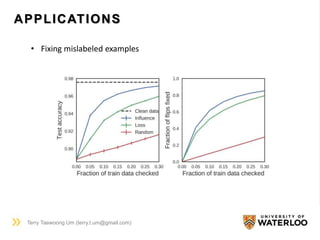
The document discusses methods for understanding predictions made by black-box models, particularly through the use of influence functions. It addresses the influence of training examples on model parameters and loss at test points, as well as techniques for handling various challenges such as non-convexity and non-differentiability. Additionally, it highlights applications for improving model behavior and debugging, including handling adversarial examples and mislabeled data.

1. Terry Taewoong Um (terry.t.um@gmail.com)
University of Waterloo
Department of Electrical & Computer Engineering
Terry T. Um
UNDERSTANDING BLACK-BOX PRED
-ICTION VIA INFLUENCE FUNCTIONS
1

2. TODAY’S PAPER
Terry Taewoong Um (terry.t.um@gmail.com)
ICML2017 best paper
https://youtu.be/0w9fLX_T6tY

3. QUESTIONS
Terry Taewoong Um (terry.t.um@gmail.com)
• How can we explain the predictions of a black-box model?
• Why did the system make this prediction?
• How can we explain where the model came from?
• What would happen if the values of a training point where
slightly changed?

4. INTERPRETATION OF DL RESULTS
Terry Taewoong Um (terry.t.um@gmail.com)
• Retrieving images that maximally activate a neuron [Girshick et al. 2014]
• Finding the most influential part from the image [Zhou et al. 2016]
• Learning a simpler model around a test point [Ribeiro et al. 2016]
But, they assumed a
fixed model
 My NN is a function
of training inputs

5. INFLUENCE OF A TRAINING POINT
Terry Taewoong Um (terry.t.um@gmail.com)
• What is the influence of a training example for
the model (or for the loss of a test example)?
Optimal model param. :
Model param. by training w/o z :
Model param. by upweighting z :
without z == (𝜖 = −
1
𝑛
)
• The influence of upweighting z on the parameters 𝜃

6. INFLUENCE OF A TRAINING POINT
• Influence vs. Euclidean distance

7. INFLUENCE OF A TRAINING POINT
Terry Taewoong Um (terry.t.um@gmail.com)
• The influence of upweighting z on the parameters 𝜃
• The influence of upweighting z on the loss at a test point

8. PERTURBING A TRAINING POINT
Terry Taewoong Um (terry.t.um@gmail.com)
• Move 𝜖 mass from 𝑧 to 𝑧 𝛿
• If x is continuous and 𝛿 is small
• The effect of 𝑧  𝑧 𝛿 on the loss at a test point

9. SUMMARY
Terry Taewoong Um (terry.t.um@gmail.com)
• The influence of 𝑧  𝑧 𝛿 on the loss at a test point
• The influence of upweighting z on the parameters 𝜃
• The influence of upweighting z on the loss at a test point

10. EXAMPLE
Terry Taewoong Um (terry.t.um@gmail.com)
• The influence of upweighting z
• In logistic regression,
• Test : 7, Train : 7 (green), 1 (red)

11. SEVERAL PROBLEMS
Terry Taewoong Um (terry.t.um@gmail.com)
• Calculation of
 Use Hessian-vector products (HVPs)

precompute 𝑠𝑡𝑒𝑠𝑡 by optimizing
or sampling-based approximation

12. SEVERAL PROBLEMS
Terry Taewoong Um (terry.t.um@gmail.com)
• What if is non-convex, so H < 0
 Assuming that is a local minimum point, define a quadratic loss
Then calculate using the above
 empirically working!
• Influence function vs. retraining

13. SEVERAL PROBLEMS
Terry Taewoong Um (terry.t.um@gmail.com)
• What if is non-differentiable?
e.g.) hinge loss
 Use a differentiable variation of the hinge loss

14. APPLICATIONS
Terry Taewoong Um (terry.t.um@gmail.com)
• Understanding model behavior

15. APPLICATIONS
Terry Taewoong Um (terry.t.um@gmail.com)
• Adversarial examples
c.f.) The effect of 𝑧  𝑧 𝛿 on the loss at a test point

16. APPLICATIONS
Terry Taewoong Um (terry.t.um@gmail.com)
• Debugging domain mismatch

17. APPLICATIONS
Terry Taewoong Um (terry.t.um@gmail.com)
• Fixing mislabeled examples