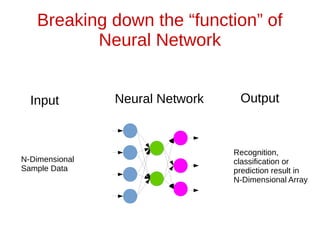
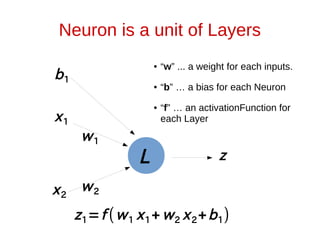
The document discusses neural networks and how they can be viewed as functions. It describes how neural networks take input data and produce output predictions or classifications. The document outlines how neural networks have a layered structure where each layer is a function, and how the layers are composed together. It explains that neurons are the basic units of computation in each layer and how they operate. The document also discusses how neural network training works by optimizing the weights and biases in each layer to minimize error, and how matrix operations in neural networks can benefit from parallel processing on GPUs.

1. Neural Network as a function
Taisuke Oe

2. Neural Network as a Function.
1.Who I am.
2.Deep Learning Overview
3.Neural Network as a function
4.Layered Structure as a function composition
5.Neuron as a node in graph
6.Training is a process to optimize states in each
layer
7.Matrix as a calculation unit in parallel in GPU

3. Who am I?
Taisuke Oe / @OE_uia
● Co-chair of ScalaMatsuri
CFP is open by 15th
Oct.
Travel support for highly voted speakers
Your sponsorship is very welcome :)
● Working in Android Dev in Scala
● Deeplearning4j/nd4s author
● Deeplearning4j/nd4j contributor
http://scalamatsuri.org/index_en.html

4. Deep Learning Overview
● Purpose:
Recognition, classification or prediction
● Architecture:
Train Neural Network parameters with
optimizing parameters in each layer.
● Data type:
Unstructured data, such as images, audio,
video, text, sensory data, web-logs
● Use case:
Recommendation engine, voice search, caption
generation, video object tracking, anormal
detection, self-organized photo album.
http://googleresearch.blogspot.ch/2015/0
6/inceptionism-going-deeper-into-
neural.html

5. Deep Learning Overview
● Advantages v.s. other ML algos:
– Expressive and accurate (e.g. ImageNet Large Scale
Visual Recognition Competition)
– Speed
● Disadvantages
– Difficulty to guess the reason of results.
Why?

6. Neural Network is a function

7. Breaking down the “function” of
Neural Network
OutputInput Neural Network
N-Dimensional
Sample Data
Recognition,
classification or
prediction result in
N-Dimensional Array

8. Simplest case:
Classification of Iris
Neural Network
Features
[5.1 1.5 1.8 3.2]
Probability of each class
[0.9 0.02 0.08]
ResultSample

9. Neural Network is like a
Function1[INDArray, INDArray]
Neural Network
Features
[5.1 1.5 1.8 3.2]
Probability of each class
[0.9 0.02 0.08]
ResultSample
W:INDArray => INDArray
W

10. Dealing with multiple samples
Neural Network
Features
[
5.1 1.5 1.8 3.2
4.5 1.2 3.0 1.2
⋮ ⋮
3.1 2.2 1.0 1.2
]
Probability of each class
[
0.9 0.02 0.08
0.8 0.1 0.1
⋮ ⋮
0.85 0.08 0.07
]
ResultsIndependent
Samples

11. Generalized Neural Network
Function
ResultsNeural Network
[
X11 X12 ⋯ X1 p
X21 X2 p
⋮ ⋮
Xn 1 Xn2 ⋯ Xnp
] [
Y11 Y12 ⋯ Y1 m
Y21 Y2 m
⋮ ⋮
Yn1 Yn2 ⋯ Ynm
]

12. NN Function deals with multiple
samples as it is (thx to Linear Algebra!)
ResultIndependent
Samples
Neural Network
[
X11 X12 ⋯ X1 p
X21 X2 p
⋮ ⋮
Xn 1 Xn2 ⋯ Xnp
] [
Y11 Y12 ⋯ Y1 m
Y21 Y2 m
⋮ ⋮
Yn1 Yn2 ⋯ Ynm
]
W:INDArray => INDArray
W

13. Layered Structure
as a function composition

14. Neural Network is a layered
structure
[
X11 X12 ⋯ X1 p
X21 X2 p
⋮ ⋮
Xn 1 Xn2 ⋯ Xnp
] [
Y11 Y12 ⋯ Y1 m
Y21 Y2 m
⋮ ⋮
Yn1 Yn2 ⋯ Ynm
]
L1 L2 L3

15. Each Layer is also a function which
maps samples to output
[
X11 X12 ⋯ X1 p
X21 X2 p
⋮ ⋮
Xn 1 Xn2 ⋯ Xnp
]
L1
[
Z11 Z12 ⋯ Z1 q
Z21 Z2 p
⋮ ⋮
Zn1 Zn2 ⋯ Znp
]
Output
of Layer1
L1 :INDArray => INDArray

16. NN Function is composed of
Layer functions.
W=L1andThenL2andThenL3
W ,L1 ,L2 ,L3 :INDArray => INDArray
[
X11 X12 ⋯ X1 p
X21 X2 p
⋮ ⋮
Xn 1 Xn2 ⋯ Xnp
] [
Y11 Y12 ⋯ Y1 m
Y21 Y2 m
⋮ ⋮
Yn1 Yn2 ⋯ Ynm
]

17. Neuron as a node in graph

18. Neuron is a unit of Layers
x1
x2
z1=f (w1 x1+ w2 x2+b1)
w1
w2
● “w” ... a weight for each inputs.
● “b” … a bias for each Neuron
● “f” … an activationFunction for
each Layer
b1
L z

19. Neuron is a unit of Layers
x1
x2
z1=f (w1 x1+ w2 x2+b1)
w1
w2
● “w” ... is a state and mutable
● “b” … is a state and mutable
● “f” … is a pure function without
state
b1
L z

20. Neuron is a unit of Layers
L
x1
z
x2
z=f( ∑
k
f (wk xk )+b )
w1
w2
● “w” ... is a state and mutable
● “b” … is a state and mutable
● “f” … is a pure function without
state
b1

21. Activation Function Examples
Relu
f (x)=max (0, x)
tanh sigmoid
-6 -4 -2 0 2 4 6
-1.5
-1
-0.5
0
0.5
1
1.5
Activation Functions
tanh sigmoid
u
z
1 2 3 4 5 6 7 8 9 10 11
0
1
2
3
4
5
6
ReLu

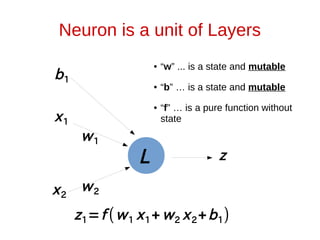
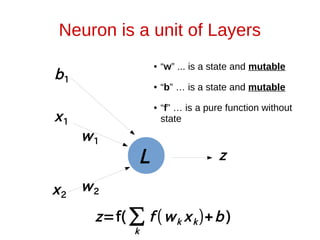
22. How does L1 function look like?
L1 (X)=( X・
[
W11 W12 ⋯ W1q
W21 W2q
⋮ ⋮
Wp1 Wp2 ⋯ Wpq
]+
[
b11 b12 ⋯ b1q
b21 b2q
⋮ ⋮
bn 1 bn 2 ⋯ bnq
]) map f
Weight Matrix Bias Matrix
L1 :INDArray => INDArray

23. L1
(
[
X11 X12 ⋯ X1p
X21 X2p
⋮ ⋮
Xn1 Xn 2 ⋯ Xnp
]・
[
W11 W12 ⋯ W1 q
W21 W2 q
⋮ ⋮
Wp1 Wp2 ⋯ Wpq
]+
[
b11 b12 ⋯ b1 q
b21 b2 q
⋮ ⋮
bn 1 bn 2 ⋯ bnq
]) map f
Input
Feature Matrix Weight Matrix Bias Matrix
=
[
Z11 Z12 ⋯ Z1 q
Z21 Z2 p
⋮ ⋮
Zn 1 Zn 2 ⋯ Znp
]
Output of Layer1
How does L1 function look like?

24. Training is a process to optimize
states in each layer

25. Training of Neural Network
● Optimizing Weight Matrices and Bias Matrices in each layer.
● Optimizing = Minimizing Error, in this context.
● How are Neural Network errors are defined?
Weight Matrix Bias Matrix
L (X)=( X・
[
W11 W12 ⋯ W1q
W21 W2q
⋮ ⋮
Wp1 Wp2 ⋯ Wpq
]+
[
b11 b12 ⋯ b1q
b21 b2q
⋮ ⋮
bn 1 bn 2 ⋯ bnq
]) map f

26. Error definition
● “e” … Loss Function, which is pure and doesn't have state
● “d” … Expected value
● “y” … Output
● E … Total Error through Neural Network
E=∑
k
e(dk , yk ) E=∑
k
|dk – yk|
2
e.g.
Mean Square Error

27. Minimizing Error by gradient decend
Weight
Error
∂ E
∂ W
Weight
Error
● “ε” ... Learning Rate, a constant or function to determine the size
of stride per iteration.
-ε ∂ E
∂ W

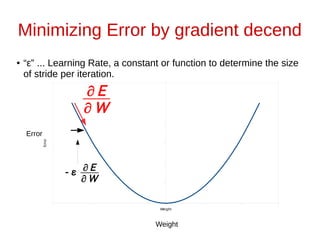
28. Minimize Error by gradient decend
● “ε” ... Learning Rate, a constant or function to determine the size
of stride per iteration.
[
W11 W12 ⋯ W1q
W21 W2q
⋮ ⋮
Wp1 Wp2 ⋯ Wpq
] -= ε
[
∂E
∂ W11
∂E
∂ W12
⋯ ∂ E
∂ W1q
∂E
∂ W21
∂ E
∂ W2q
⋮ ⋮
∂E
∂ Wp1
∂E
∂ Wp2
⋯ ∂ E
∂ Wpq
]
[
b11 b12 ⋯ b1q
b21 b2q
⋮ ⋮
bp1 Wp2 ⋯ bpq
] -= ε
[
∂ E
∂ b11
∂ E
∂ b12
⋯ ∂ E
∂ b1q
∂ E
∂ b21
∂ E
∂ b2q
⋮ ⋮
∂ E
∂bp1
∂ E
∂bp2
⋯ ∂ E
∂ bpq
]

29. Matrix as a calculation unit
in parallel in GPU

30. Matrix Calculation in Parallel
● Matrix calculation can be run in parallel, such as multiplication,
adding,or subtraction.
● GPGPU works well matrix calculation in parallel, with around
2000 CUDA cores per NVIDIA GPU and around 160GB / s
bandwidth.
[
W11 W12 ⋯ W1 q
W21 W2 q
⋮ ⋮
Wp1 Wp 2 ⋯ Wpq
] -= ε
[
∂ E
∂ W11
∂ E
∂ W12
⋯
∂ E
∂ W1 q
∂ E
∂ W21
∂ E
∂ W2 q
⋮ ⋮
∂ E
∂ Wp 1
∂ E
∂ Wp 2
⋯ ∂ E
∂ Wpq
]
(
[
X11 X12 ⋯ X1p
X21 X2p
⋮ ⋮
Xn1 Xn2 ⋯ Xnp
]・
[
W11 W12 ⋯ W1q
W21 W2q
⋮ ⋮
Wp 1 Wp2 ⋯ Wpq
]+
[
b11 b12 ⋯ b1q
b21 b2q
⋮ ⋮
bn1 bn2 ⋯ bnq
]) map f

31. DeepLearning4j
● DeepLearning Framework in JVM.
● Nd4j for N-dimensional array (incl. matrix) calculations.
● Nd4j calculation backends are swappable among:
● GPU(jcublas)
● CPU(jblas, C++, pure java…)
● Other hardware acceleration(OpenCL, MKL)
● Nd4s provides higher order functions for N-dimensional Array