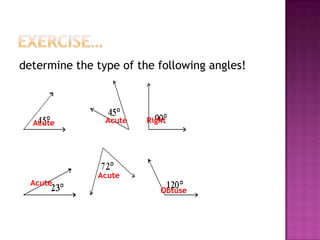
Here are the questions rewritten in hexadecimal system: 1. Find the angle formed by the hour and minute hands of a clock at 10:45. 2. Find the angle formed by the hour and minute hands of a clock at 5:15. 3. Find the angle formed by the hour and minute hands of a clock at 2:30. 4. Find the angle formed by the hour and minute hands of a clock at 11:30. 5. Find the angle formed by the hour and minute hands of a clock at 7:00. Back

1. BY : RONALD N S

2.  Full turn : satu putaran penuh(360o)
 Straight angle : sudut lurus ( 180o)
 Right angle : sudut siku-siku ( 90o)
 Acute angle : sudut lancip (0o < x < 90o)
 Obtuse angle : sudut tumpul (90o< x <180o)
 Reflex angle : sudut refleks (180o < x < 360o)
 Protractor : busur derajat
 Magnitude : besaran, ukuran
 Longest arm (minute arm) : jarum panjang
 short arm ( hour arm ) : jarum pendek
 Complemantary angle : sudut berpenyiku
 Supplementary angle : sudut berpelurus
 Vertically opposite : bertolak belakang
 Intersect : Berpotongan
 Compasses : Jangka
 Perpendicular : tegak lurus
 Bisector : Membagi sudut sama besar

3. Types of Angles
Parts of Angle Hexadecimal system
Supplementary Angles
Labelling Angles
Complementary Angles Clock Angle Problem

4.  The corner point of an
angle is called the
VERTEX
 Two straight lines is
called ARMS
The angle is the amount
of turn between each
Back
arm.

5.  There are two main ways to label
angles:
1. by giving the angle a name,
usually a lower-case letter like a
or b, or sometimes a Greek letter
like α (alpha) or θ (theta)
2. or by the three letters on the
shape that define the angle, with
the middle letter being where the
angle actually is (its vertex).
Example angle "a" is "BAC", and
angle "θ" is "BCD"
Back

6. Back
Look at the picture, and completely the table!
B G
2
D
4
C 3
1 F
5
A E
H
Numbers One letter Three letters
1 A BAC
2 B ABC
3 F GFH
4 G FGH
5 H FHG

7. Back
Type of Angle Description
Acute angle an angle that is less than 90°
Right angle an angle that is 90° exactly
Obtuse angle an angle that is greater than 90° but less than 180°
Straight angle an angle that is 180° exactly
Reflex angle an angle that is greater than 180°

8. determine the type of the following angles!
Acute Acute Right
Acute
Acute
Obtuse

9. Two Angles are Complementary if they add up
to 90 degrees (a Right Angle).
These two angles (40° and 50°)
are Complementary Angles,
because they add up to 90°.
If the two angles add to 90°, we say they "Complement" each other.
Back

10. Two Angles are Supplementary if they add up
to 180 degrees.
These two angles (140° and 40°)
are Supplementary Angles, because
they add up to 180°.
If the two angles add to 180°, we say they "Supplement" each other.
Back

11. How can you remember which is which? Easy!
Think:
 "C" of Complementary stands for "Corner"
(a Right Angle), and
 "S"of Supplementary stands for "Straight"
(180 degrees is a straight line)

12. Remember :
1o = 60 ‘ 1‘ = ( 1/ 60 )o
1‘ = 60 “ 1“ = ( 1 / 60)‘
1o = 3600’’ 1’’ = ( 1/ 3600 )o
O read degree
‘ read minute
“ read second

13. Rewrite 3,15 o into the hexadecimal system!
Solution
3,15o = 3o + 0,15o
= 3o + 0,15 x 1o
= 3o + 0,15 x 60’
= 3o + 9’
= 3o9’
So, 3,15o = 3o9’

14. Rewrite 3,125o into hexadecimal system!
Solution
3,125o = 3o + 0,125o
= 3o + 0,125 x 1o
= 3o + 0,125 x 60’
= 3o + 7,5’
= 3o + 7’ + 0,5’
= 3o+ 7’ + 0,5 x 60’’
= 3o + 7’ + 30’’
= 3o7’30’’

15. Rewrite 19o15’27’’ in degree unit!
19o15’27’’ = …..o
= 19o + 15’ + 27’’
= 19o + 15 x ( 1/60)o + 27 x ( 1/3600)o
= 19o + 0,25o + 0,0075o
= 19,2575o
So, 19o15’27’’ = 19,2575o

16. Find the result :
a. 15o43’25’’ + 42o52’17’’
b. 42o17’52’’ – 25o34’44’’

17. a. 15o43’25’’
42o52’17’’ +
57o95’42’’ = 58o35’42’’
b. 42o17’52’’ 41o77’52’’
25o34’44’’ - 25o34’44’’ -
16o43’8’’
Back

18.  The hour hand of a normal 12-hour analogue
clock turns 360° in 12 hours (720 minutes)
or 0.5° per minute
 Theminute hand rotates through 360° in 60
minutes or 6° per minute.
Back

19. From this statement , we can write :
a) Long arm = minute arm
1 hour = 60’ = 360o
1 minute = 360o : 60 = 6o
b) Short arm = hour arm
1 hour = 360o : 12 = 30o
1 minute = 30o : 60 = 0,5o

20. What degree is the angle formed by long and
short arm of analogue clock at 07.15 am?
Solution:
Position long arm in number 3
Position short arm in number 7
So,
(7 – 3)x 30o = 4 x 30o = 120o
Then Short arm is move = 15 x 0,5o = 7,5o
So, angle formed = 120o + 7,5o = 127,5o

22. Rewrite these questions into hexadecimal
system: